
Chapter 5 Stucture of polyatomic molecules (A) 5.1 Theory of hybrid orbital and atomic orbital hybridization 1.Theory of hybrid orbital Two Theories of Bonding MOLECULAR ORBITAL THEORY valence electrons are delocalized valence electrons spread over entire molecule. VALENCE BOND THEORY 。 valence electrons are localized between atoms (or are lone pairs). half-filled atomic orbitals overlap to form bonds
Chapter 5 Stucture of polyatomic molecules (A) MOLECULAR ORBITAL THEORY MOLECULAR ORBITAL THEORY • valence electrons are valence electrons are delocalized delocalized • valence electrons spread over entire molecule. valence electrons spread over entire molecule. Two Theories of Bonding Two Theories of Bonding VALENCE BOND THEORY VALENCE BOND THEORY • valence electrons are valence electrons are localized localized between atoms (or are between atoms (or are lone pairs). lone pairs). • half-filled atomic filled atomic orbitals orbitals overlap to form bonds. overlap to form bonds. §5.1 Theory of hybrid orbital and atomic orbital hybridization 1. Theory of hybrid orbital

Central Themes of Valence Bond Theory Basic Principle of Valence Bond Theory:a covalent bond forms when the orbitals from two atoms overlap and a pair of electrons occupies the region between the nuclei. 1)Opposing spins of the electron pair. 2)Maximum overlap of bonding orbitals. 3)Hybridization of atomic orbitals. Pauling proposed that the valence atomic orbitals in the molecule are different from those in the isolated atoms.We call this Hybridization! Why do atomic orbital need hybridization? H20 Each o bond arises from the overlap of an H1s orbital with one of the O2p orbitals.This ●H model suggests that the bond angle should be9o°,which is significantly different from the experimental value. Use of p-orbitals
Central Themes of Valence Bond Theory 1) Opposing spins of the electron pair. 2) Maximum overlap of bonding orbitals. 3) Hybridization of atomic orbitals. Pauling proposed that the valence atomic orbitals in the molecule are different from those in the isolated atoms. We call this Hybridization! Basic Principle of Valence Bond Theory: a covalent bond forms when the orbitals from two atoms overlap and a pair of electrons occupies the region between the nuclei. Use of p - orbitals H2O Why do atomic orbital need hybridization? Each σ bond arises from the overlap of an H1s orbital with one of the O2p orbitals. This model suggests that the bond angle should be 90°, which is significantly different from the experimental value
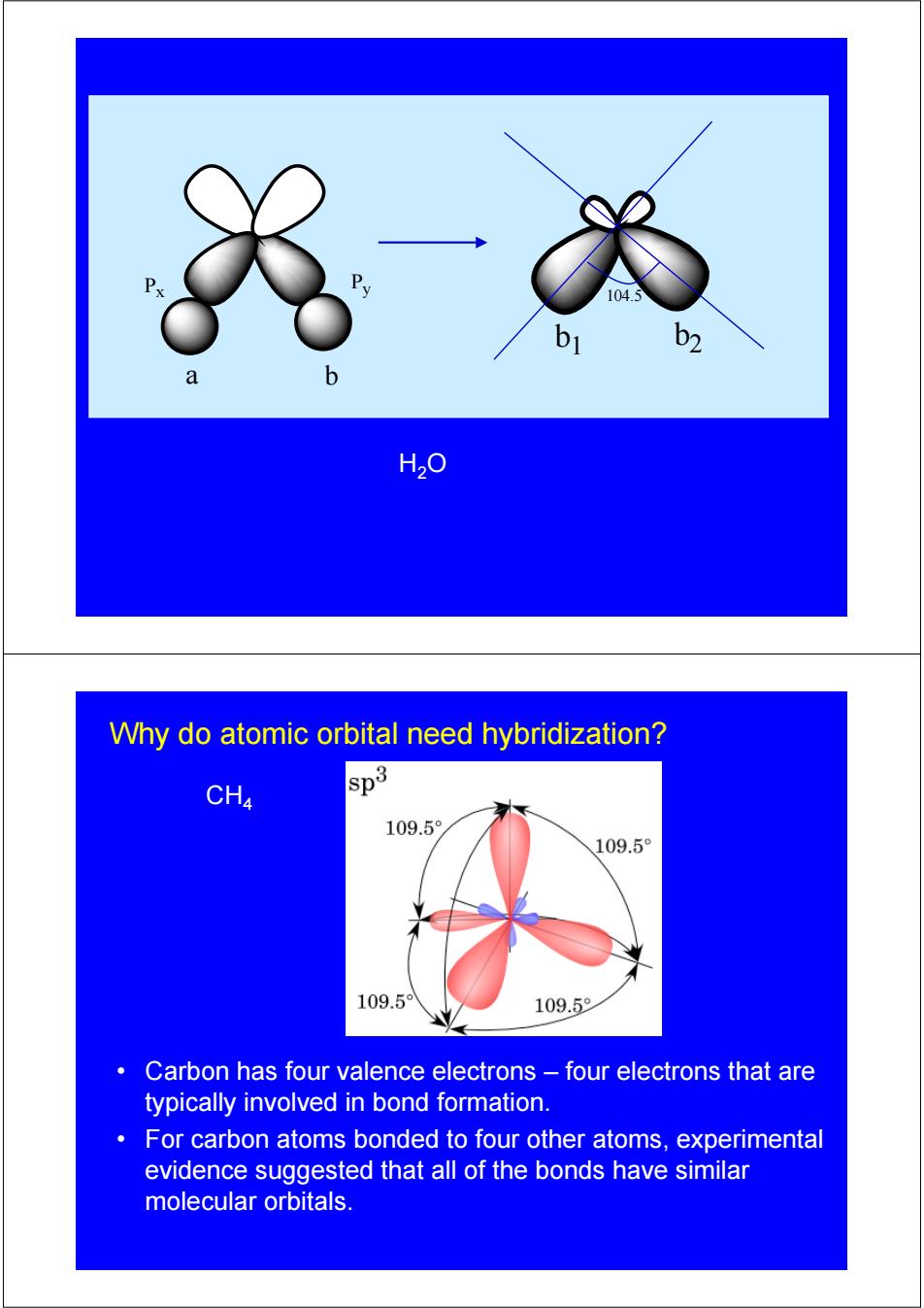
P 104.5 b1 b2 H2O Why do atomic orbital need hybridization? CH4 sp3 109.5 109.5° 109.5 109.5 Carbon has four valence electrons four electrons that are typically involved in bond formation. For carbon atoms bonded to four other atoms,experimental evidence suggested that all of the bonds have similar molecular orbitals
Px Py a b 104.5 b1 b2 H2O • Carbon has four valence electrons – four electrons that are typically involved in bond formation. • For carbon atoms bonded to four other atoms, experimental evidence suggested that all of the bonds have similar molecular orbitals. CH4 Why do atomic orbital need hybridization?

b.How do atomic orbital hybridize? 中n=C中,+C22m+C3中2py+C4中2pr If we begin with n AO's,we must end up with n orbitals after hybridization. All n hybrids are equivalent except for directionality same energy. 2.Construction of hybrid orbitals
b. How do atomic orbital hybridize? h s px py pz c c c c φ = 1 φ2 + 2φ2 + 3 φ2 + 4φ2 If we begin with n AO’s, we must end up with n orbitals after hybridization. All n hybrids are equivalent except for directionality Æ same energy. 2. Construction of hybrid orbitals

a.sp hybridization (linear species) One s and one p AO mix to form a set of two hybrid orbitals. 2s sp hybrid 2Px sp hybrid -+ sp,0=l80°,linear, Normalization and orthogonality 0h2 1V2 s b.sp2 hybridization (trigonal planar) One s and two p(Px and py)AO's mix to form a set of three 30 hybrid orbitals. 1 2 <30! 1 25 h2 sp2,Dh,0=l20°,triangular, f=1.991,=1/3 h
a. sp hybridization (linear species) • One s and one p AO mix to form a set of two hybrid orbitals. ( ) 2 1 ( ) 2 1 2 2 1 2 h s px h s px φ φ φ φ φ φ = − = + sp, θ=180°, linear, Normalization and orthogonality h s px py h s px py h s px 3 2 2 2 2 2 1 2 2 1 6 1 3 1 2 1 6 1 3 1 3 2 3 1 φ φ φ φ φ φ φ φ φ φ φ = − − = − + = + • One s and two p (px and py) AO’s mix to form a set of three hybrid orbitals. b. sp2 hybridization (trigonal planar) sp2, D3h, θ=120°, triangular, f=1.991, α=1/3 φh1 φh2 φh3 x y

=a,,+b,中2x+C,02pmy For equivalent hybridization:the weighting of s orbital in each hybrid orbital is 1/3,and therefore a,=V1/3 中i=V1/34,+b,42m+C,中2py Supposed is parallel to the x-axis and is perpendicular to the y-axis 中n1=V1/30,+b,2m Normalization 中a1=V1/30,+V2/30 中1=V1/30+√21342x 中n=V1/30,+b,2x+C,py Normalization and orthogonality a,2+b2+c,2=1 2 1/3+b,2+c,2-1 a1a2+b,b2+cc2=0 1/3+√2/3b2+0c2=0 b2=-1/6 C2=±V1/2 h2 =V1/3。-1/642x+1/24p =V1/30,-V1/64m-V1/24m
hi i s i px i py a b c φ = φ + φ2 + φ2 For equivalent hybridization: the weighting of s orbital in each hybrid orbital is 1/3, and therefore = 1/ 3 i a Supposed φh1 is parallel to the x-axis and is perpendicular to the y-axis. h s px h s i px b 1 2 1 2 1/ 3 2 / 3 1/ 3 φ φ φ φ φ φ = + = + Normalization hi s i px i py b c 2 2 φ = 1/ 3φ + φ + φ hi s i px i py b c 2 2 φ = 1/ 3φ + φ + φ h1 s 3 2 px φ = 1/ 3φ + 2 / φ Normalization and orthogonality 1/ 3 2 / 3 0 0 1/ 3 1 2 2 2 2 2 2 + + ⋅ = + + = b c b c 0 1 1 2 1 2 1 2 2 2 2 2 2 2 + + = + + = a a b b c c a b c b2 = − 1/ 6 c2 = ± 1/ 2 h2 s 2 px 2 py φ = 1/ 3φ − 1/ 6φ + 1/ 2φ h3 s 2 px 2 py φ = 1/ 3φ − 1/ 6φ − 1/ 2φ
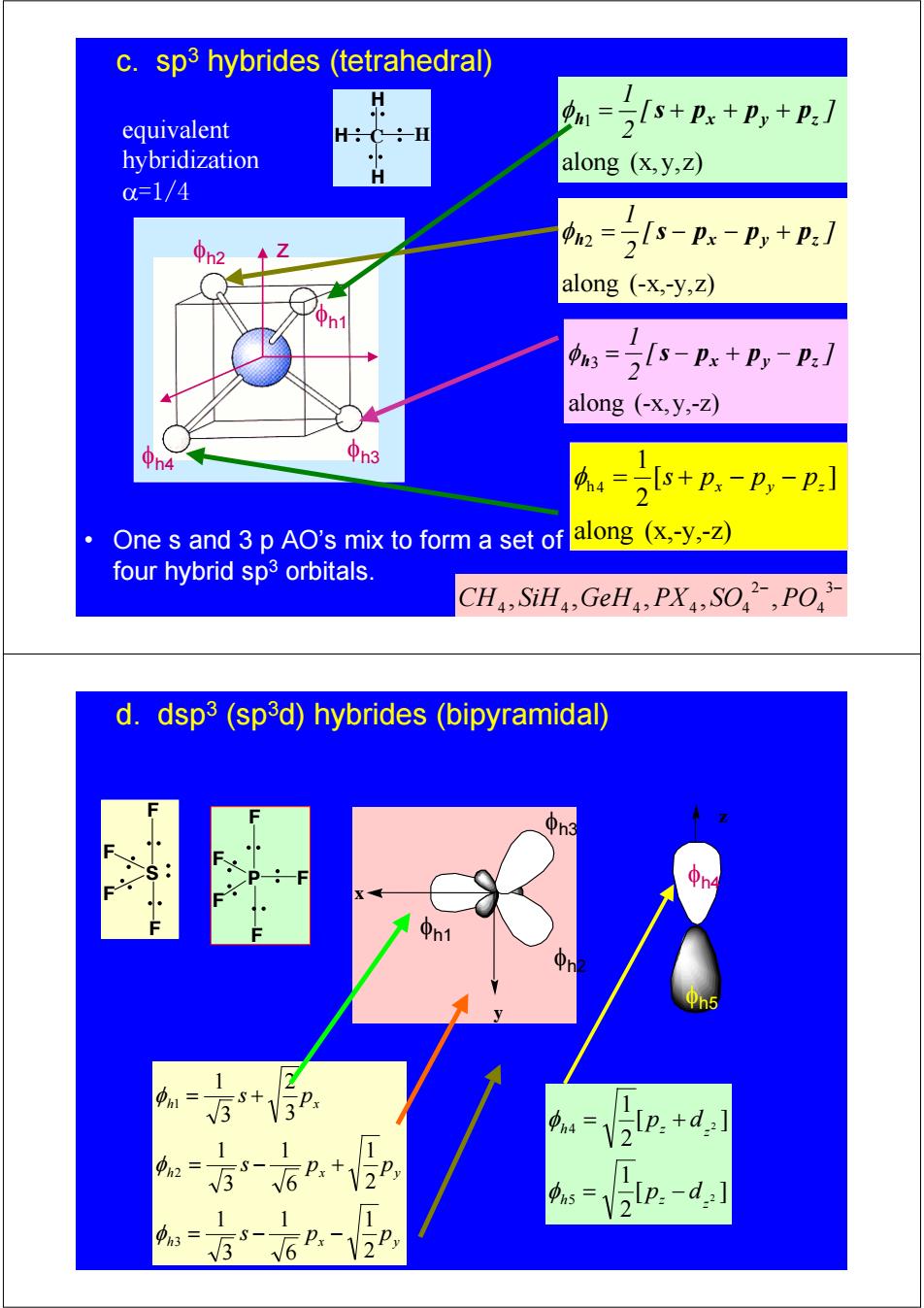
c.sp3 hybrides (tetrahedral) equivalent 1= 2+px+p,+P:] -H hybridization H along (x,y,z) c=1/4 2 22s-n-p,+:/ along (-x,-y,Z) 1 :=2s-Px+P,-P:] along (-x,y,-Z) h4 中n3 s+px -Py-p: 2 One s and 3 p AO's mix to form a set of along (x,-y,-Z) four hybrid sp3 orbitals. CH,SiH,GeHa,PX,SO,PO d.dsp3(sp3d)hybrides (bipyramidal) n3 1 m= 1 =V2Ip.+d:] 0h2= 12 Vlp:-d:] 1 1 S- 3 6 Px 2
H C H H H φh1 φh2 φh4 φh3 z along (-x,-y,z) 2 [ ] 2 1 h px py pz φ = s − − + along (x, y,z) 1 [ ] 2 1 h x y z φ = s + p + p + p along (x,-y,-z) [ ] 2 1 h 4 x y z φ = s + p − p − p along (-x,y,-z) 3 [ ] 2 1 h px py pz φ = s − + − • One s and 3 p AO’s mix to form a set of four hybrid sp3 orbitals. equivalent hybridization α=1/4 c. sp3 hybrides (tetrahedral) − 3− 4 2 4 4 4 4 4 CH , SiH ,GeH , PX , SO , PO P F F F F F h x y h x y h x s p p s p p s p 2 1 6 1 3 1 2 1 6 1 3 1 3 2 3 1 3 2 1 = − − = − + = + φ φ φ φh1 φh2 x y φh3 [ ] 2 1 [ ] 2 1 2 2 5 4 z h z z h z p d p d = − = + φ φ φh4 φh5 z S F F F F d. dsp3 (sp3d) hybrides (bipyramidal)
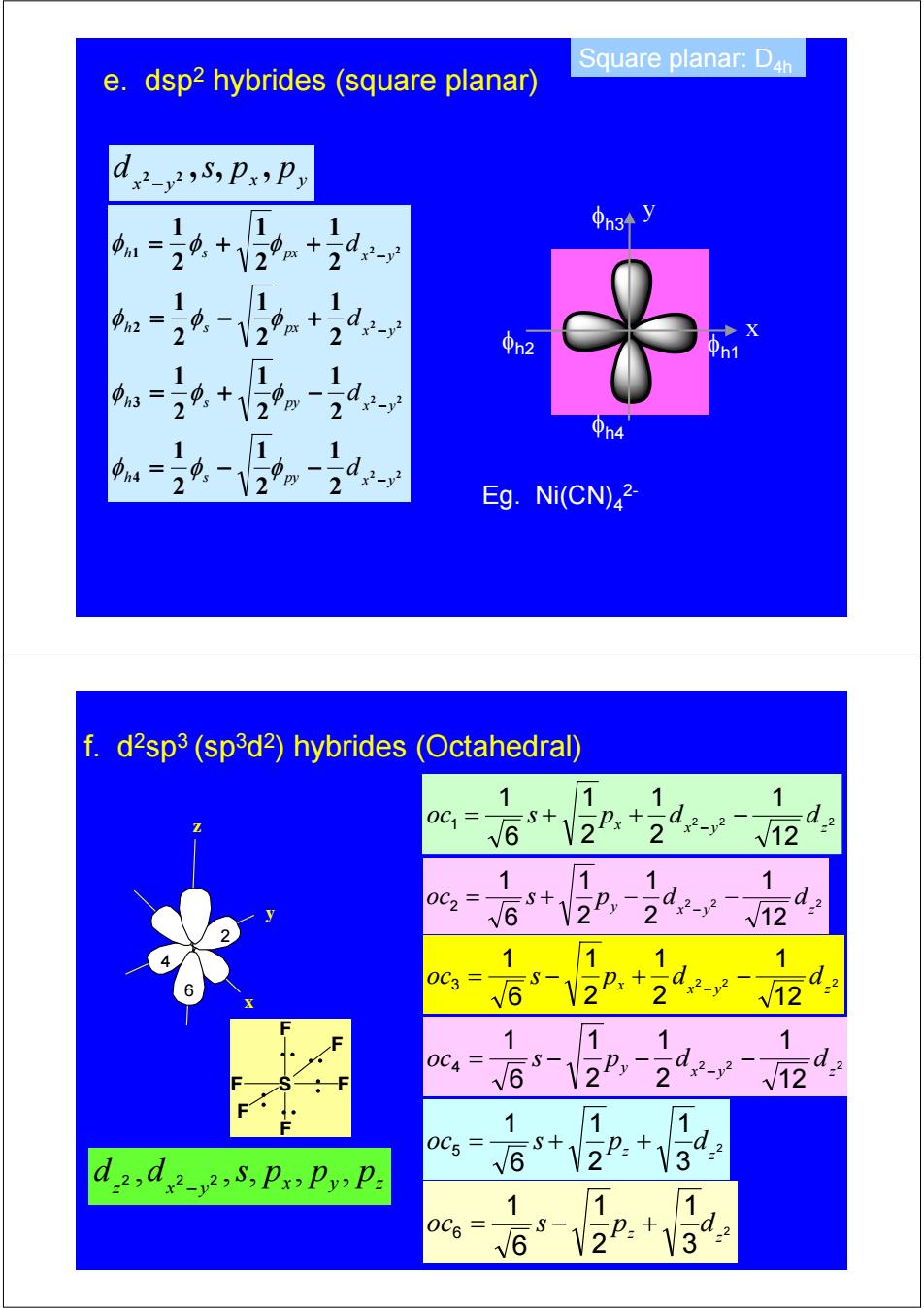
Square planar:D4h e.dsp2 hybrides (square planar) 中1= 9 d: φn2 h2 中n31 2 2 2 Eg.Ni(CN)2- f.d2sp3 (sp3d2)hybrides (Octahedral) 1 1 0G6+22.+24 V12 11 1 oc=65+12P, d2- 2V12 11 6-2+ -dz 1 11 oc=16-V2P,-2d2 1 0C5 =S十 d2 dd5,PxPyP= √ 1 1 0C6 √6 2P+3
Square planar: D4h 2 2 2 2 2 2 2 2 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 4 3 2 1 h s py x y py x y h s px x y h s px x y h s d d d d − − − − = − − = + − = − + = + + φ φ φ φ φ φ φ φ φ φ φ φ x y x y d 2 2 ,s, p , p − φh1 x y φh3 φh2 φh4 Eg. Ni(CN)4 2- e. dsp2 hybrides (square planar) 5 1 2 3 4 6 x y z 2 3 1 2 1 6 1 5 z z oc = s + p + d 2 2 2 12 1 2 1 2 1 6 1 1 x y z oc = s + px + d − d − 2 2 2 12 1 2 1 2 1 6 1 2 x y z oc = s + py − d − d − 2 2 2 12 1 2 1 2 1 6 1 3 x y z oc = s − px + d − d − 2 2 2 12 1 2 1 2 1 6 1 4 x y z oc = s − py − d − d − 2 3 1 2 1 6 1 6 z z oc = s − p + d x y z z x y d 2 ,d 2 2 ,s, p , p , p − f. d2sp3 (sp3d2) hybrides (Octahedral) F S F F F F F

Hybridization schemes spndm gives a“complete'”set of hybrid orbitals for“any”geometry. sp linear sp2 trigonal planar sp3 tetrahedral sp3d (d,2) trigonal bipyramidal sp3d(d,2-y2) square-based pyramidal sp3d2 octahedral sp2d square planar 3.The angle between two hybrid orbital spn hybridation 4n=Va02、+V1-a42p 中m=Va功,+V1-a,2n ,=Va中,+V1-a,4p whereφnmis 中p=X,中x+y,02py+2,02p
Hybridization schemes spndm gives a “complete” set of hybrid orbitals for “any” geometry. sp octahedral 3d2 sp trigonal bipyramidal 3d (dz 2) square-based pyramidal sp3d(dx 2-y 2) sp square planar 2d sp tetrahedral 3 sp trigonal planar 2 sp linear 3. The angle between two hybrid orbital spn hybridation h 2s 2 p φ = αφ + 1−αφ p j φh j = α j φ2s + 1−α j φ2 pi hi i 2s i 2 φ = α φ + 1−α φ p i px i py i pz x y z i φ = φ + φ2 + φ2 where φpi is

Normalization and orthogonality 0=∫44,dr=∫(Va4+V1-g)(Wa4,+V1-cgn)dr -aaSdr+(1-@)-@)o.dr+0+0 O-aa,+/(1-a)(-@,)cose aa V1-a)0-a) (c0s00,0>90°) Equivalent hybridzation.Example:CH4 i≠0j Non-equivalent hybridzation.Example:CHCl3,CHaCl Equivalent hybridization sp3-hybrides 1 Q= 4 1 aaj 4 1 V1-a,1-a) 3 4 sp3 0=10928" 109.5 109.5° 109.59 109.5
(1 )(1 ) cos 0 (1 )(1 ) cos (1 )(1 ) 0 0 0 ( 1 )( 1 ) 2 2 2 2 i j i j ij i j i j ij i j s i j pi pj hi hj i s i pi j s j pj d d d d α α αα θ αα α α θ αα φ τ α α φ φ τ φ φ τ αφ αφ α φ α φ τ − − =− = + − − = + − − + + = = + − + − ∫ ∫ ∫ ∫ Equivalent hybridzation. Example: CH4 Non-equivalent hybridzation. Example: CHCl3, CH3Cl i j i j α α α α ≠ = (cosθij90°) φ hi φ hj θ ij Normalization and orthogonality sp3 − hybrides 109 28" 3 1 4 3 4 1 (1 )(1 ) cos 4 1 0 = = − = − − − = − = θ α α α α θ α i j i j ij Equivalent hybridization