
Chapter 7 Introduction to Crystallography Diamonds
Chapter 7 Chapter 7 Introduction to Introduction to Crystallography Crystallography Diamonds

7.1 periodicity and lattices of crystal structure 7.1.1 The characteristics of crystal structure 1.A few definitions: Solids can be divided into to primary categories, crystalline and amorphous. Crystalline Solids that are built from atoms or molecules arranged in a periodic manner in space. Amorphous Solids posses short range order only. They are not related through symmetry. Short Range Order:Fixed bond lengths and angles Long Range Order:Associated with a lattice point Crystals: Crystals are solids that are built from atoms or molecules arranged in a periodic manner in space. Crystalline vs.Amorphous of SiO2 Quartz:(Crystalline) Glass:(Amorphous) Both Short and Long Range Order Short Range Order Only Oxygen Silicon
7.1 periodicity and lattices of crystal structure 7.1.1 The characteristics of crystal structure 1. A few definitions: • Solids can be divided into to primary categories, crystalline and amorphous. • Crystalline Solids that are built from atoms or molecules arranged in a periodic manner in space. • Amorphous Solids posses short range order only. They are not related through symmetry. • Short Range Order: Fixed bond lengths and angles • Long Range Order: Associated with a lattice point Crystals: Crystals: Crystals are solids that are built from atoms or Crystals are solids that are built from atoms or molecules arranged in a periodic manner in space. molecules arranged in a periodic manner in space

2.Fundamental characteristics of crystal .Spontaneous formation of polyhedral shapes F+V=E+2 Dodecahedron Icosahedron Cube 20 faces and 12 vertices Octahedron Tetrahedron Single crystal gold bead with naturally formed facets
2. Fundamental characteristics of crystal •Spontaneous formation of polyhedral shapes F+V=E+2 Single crystal gold bead with naturally formed facets

H 1010· .rooind 100nm 100nm HRTEM images of hollow beads •Anisotropy 2150g/mm2 Conductivity 1150g/mm2 570g/mm2 Graphite NaCl
HRTEM images of hollow beads •Anisotropy NaCl 570 g/mm2 1150 g/mm2 2150 g/mm2 Graphite Conductivity

.Definite sharp melting points ·Symmetry -X-ray diffraction by crystals 7.1.2 The lattice and unit cell ·Lattice: A periodic pattern of points in space,such that each lattice point has identical surroundings. 。 Can be reproduced by translational motion along the vector between any two points
• Symmetry •Definite sharp melting points •X-ray diffraction by crystals t T 7.1.2 The lattice and unit cell • Lattice: • A periodic pattern of points in space, such that each lattice point has identical surroundings. • Can be reproduced by translational motion along the vector between any two points

a.The lattice and its unit in 1D: T=ma(m=0,±1,±2,.…) 5 )⊙⊙ ⊙ ,· ● Figure 1.13 A one-dimensional lattice. unit cell and its choice for one-dimensional lattice One dimensional lattice
a. The lattice and its unit in 1D: T = ma (m = 0, ±1, ± 2,…) unit cell and its choice for one-dimensional lattice One dimensional lattice
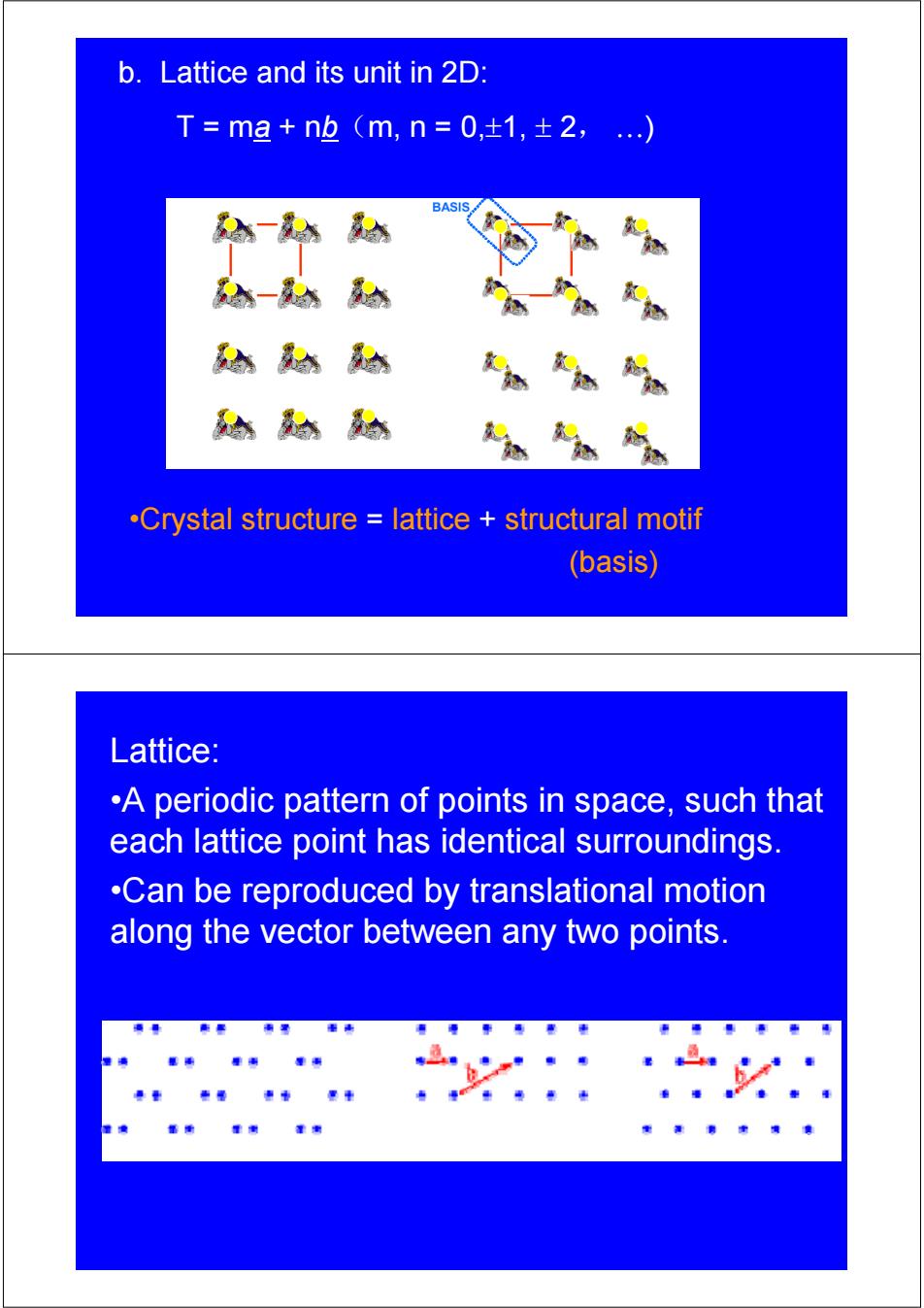
b.Lattice and its unit in 2D: T=ma+nb(m,n=0,±1,±2,.…) BASIS .Crystal structure lattice structural motif (basis) Lattice: .A periodic pattern of points in space,such that each lattice point has identical surroundings. .Can be reproduced by translational motion along the vector between any two points
b. Lattice and its unit in 2D: T = ma + nb(m, n = 0,±1, ± 2, …) •Crystal structure = lattice + structural motif (basis) Lattice: •A periodic pattern of points in space, such that each lattice point has identical surroundings. •Can be reproduced by translational motion along the vector between any two points
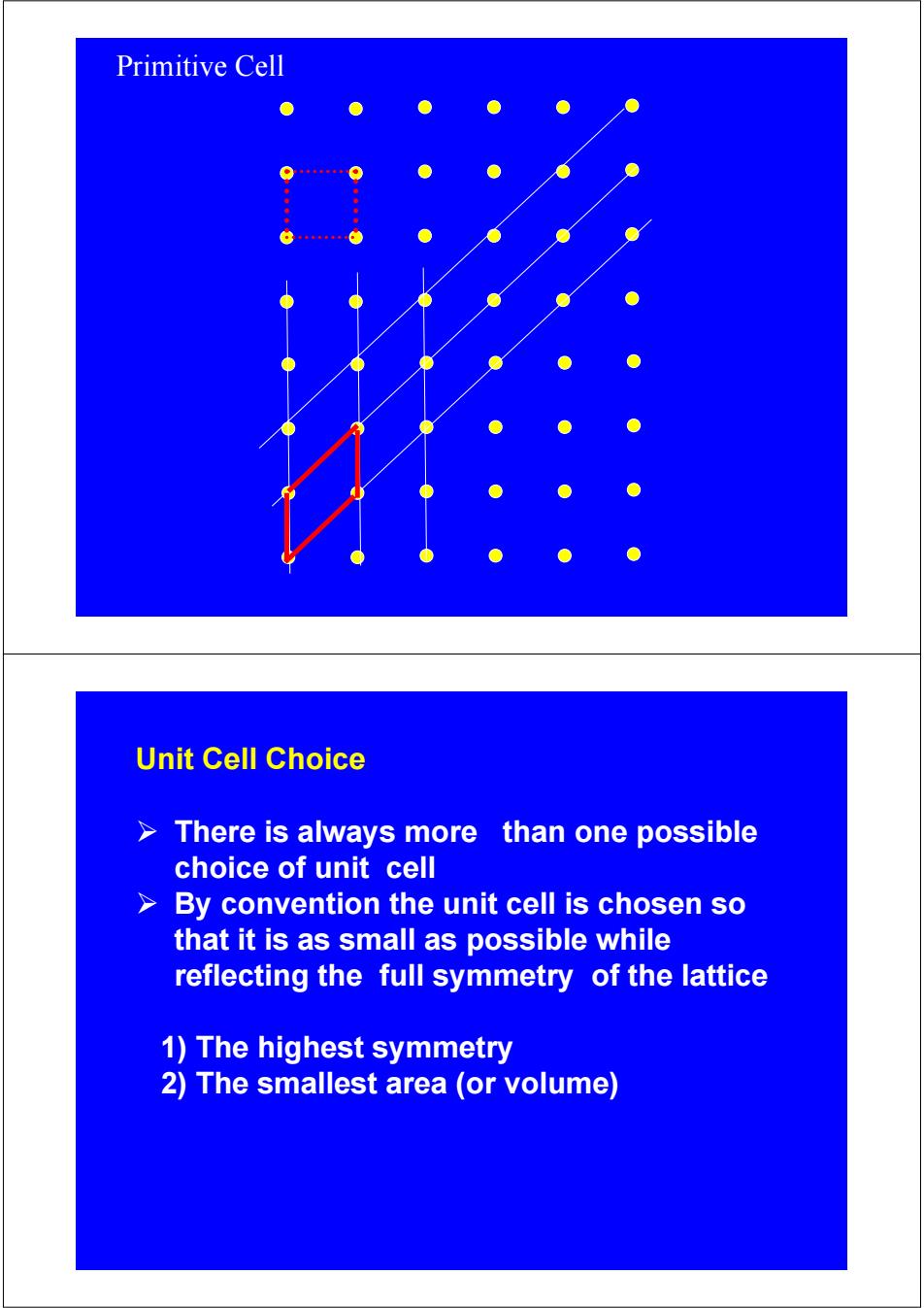
Primitive Cell Unit Cell Choice There is always more than one possible choice of unit cell > By convention the unit cell is chosen so that it is as small as possible while reflecting the full symmetry of the lattice 1)The highest symmetry 2)The smallest area (or volume)
Primitive Cell Unit Cell Choice ¾ There is always more than one possible choice of unit cell ¾ By convention the unit cell is chosen so that it is as small as possible while reflecting the full symmetry of the lattice 1) The highest symmetry 2) The smallest area (or volume)
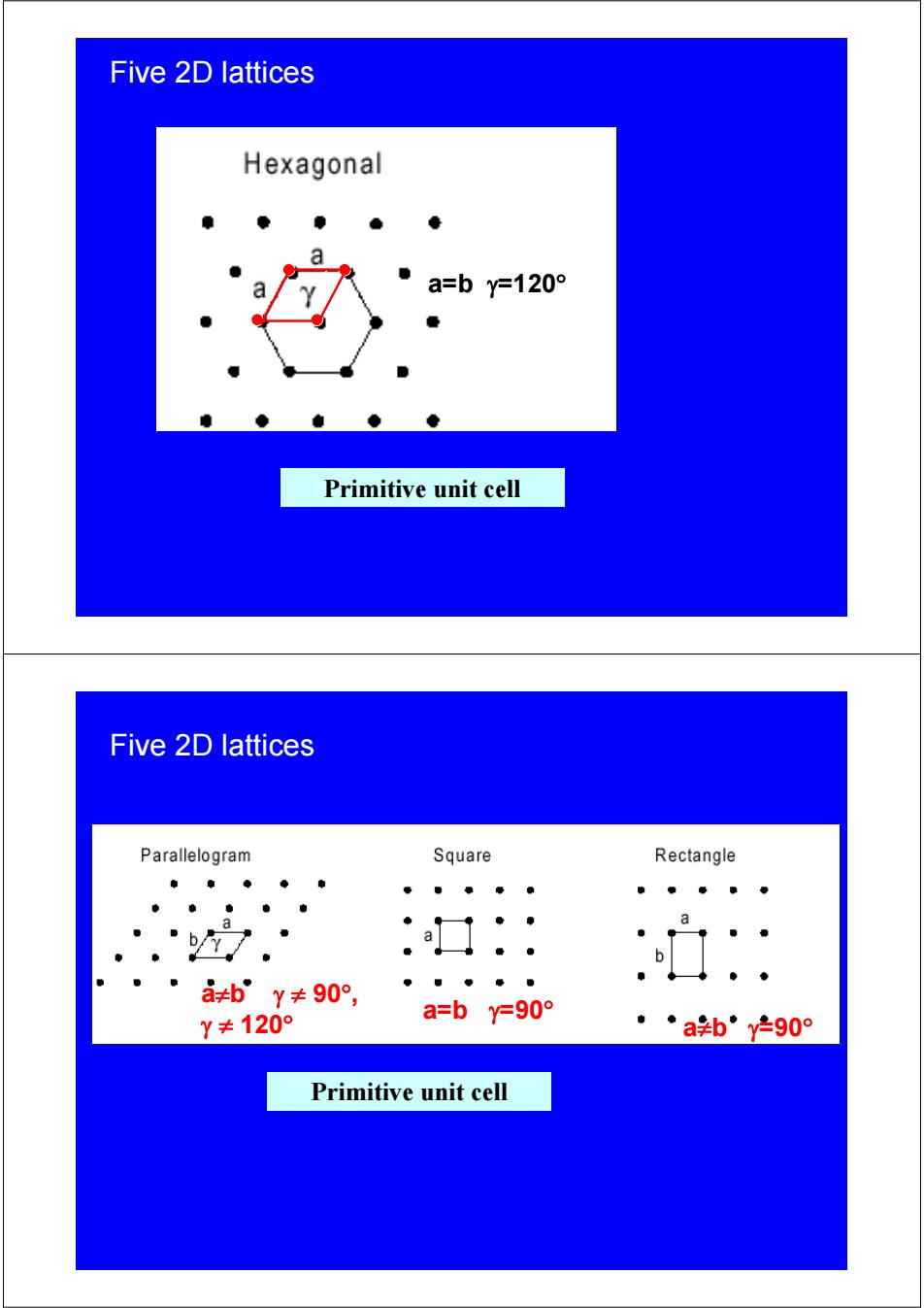
Five 2D lattices Hexagonal a=by=120° Primitive unit cell Five 2D lattices Parallelogram Square Rectangle a a≠bY≠90°, Y≠120° a=by=90° ◆ab”y-90° Primitive unit cell
Five 2D lattices a=b γ=120° Primitive unit cell Five 2D lattices a=b γ=90° a≠b γ=90° a≠b γ ≠ 90° , γ ≠ 120° Primitive unit cell
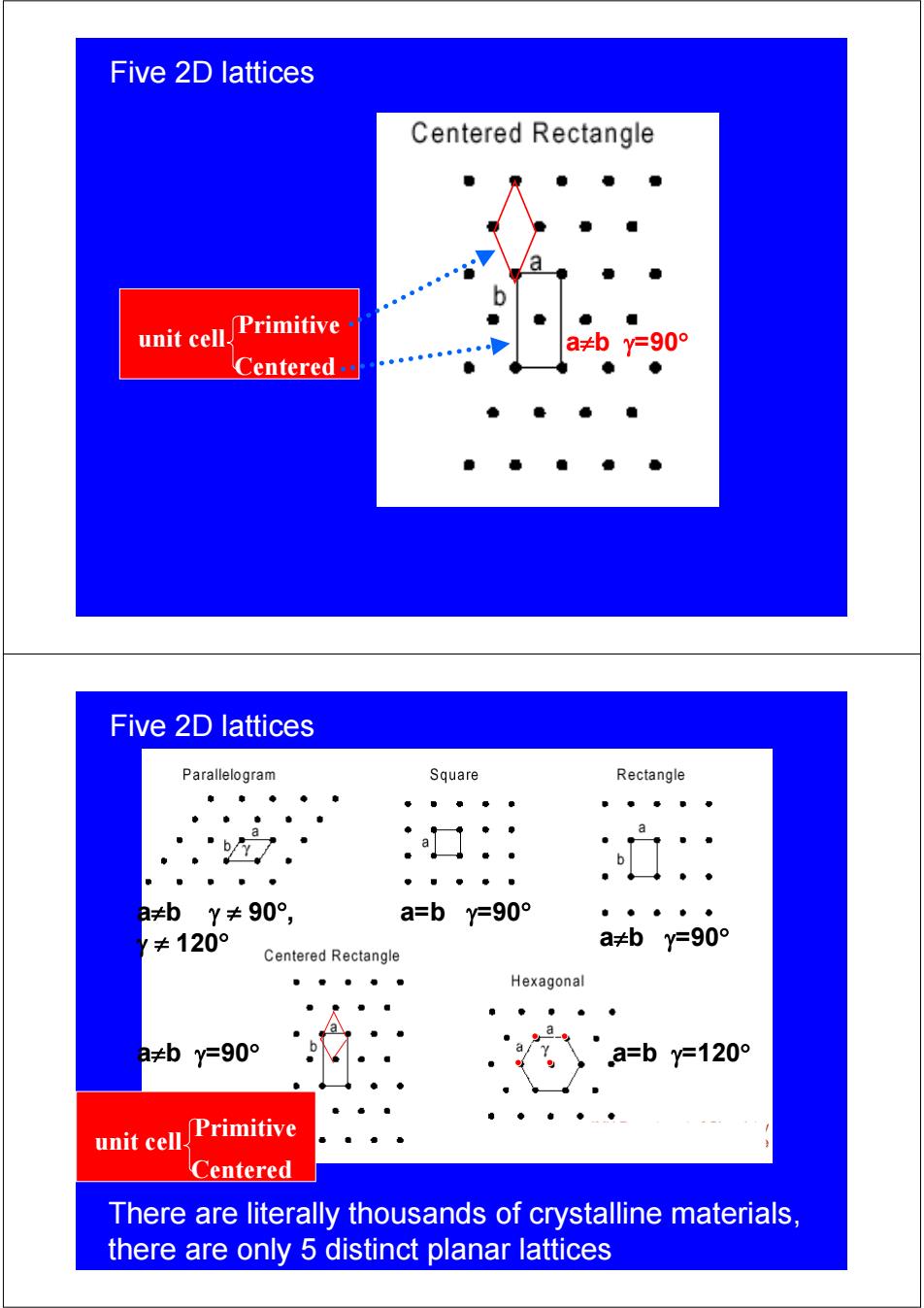
Five 2D lattices Centered Rectangle unit cell. Primitive a≠by=90° Centered Five 2D lattices Parallelogram Square Rectangle a b 日≠bY≠90°, a=by=90° ≠120° a≠by=90° Centered Rectangle Hexagonal a 2≠by=90° a=by=120° unit cell. Primitive Centered There are literally thousands of crystalline materials, there are only 5 distinct planar lattices
Five 2D lattices unit cell a≠b γ=90° Centered Primitive Five 2D lattices a=b γ=90° a≠b γ=90° a≠b γ=90° a=b γ=120° a≠b γ ≠ 90° , γ ≠ 120° unit cell Centered Primitive There are literally thousands of crystalline materials, there are only 5 distinct planar lattices