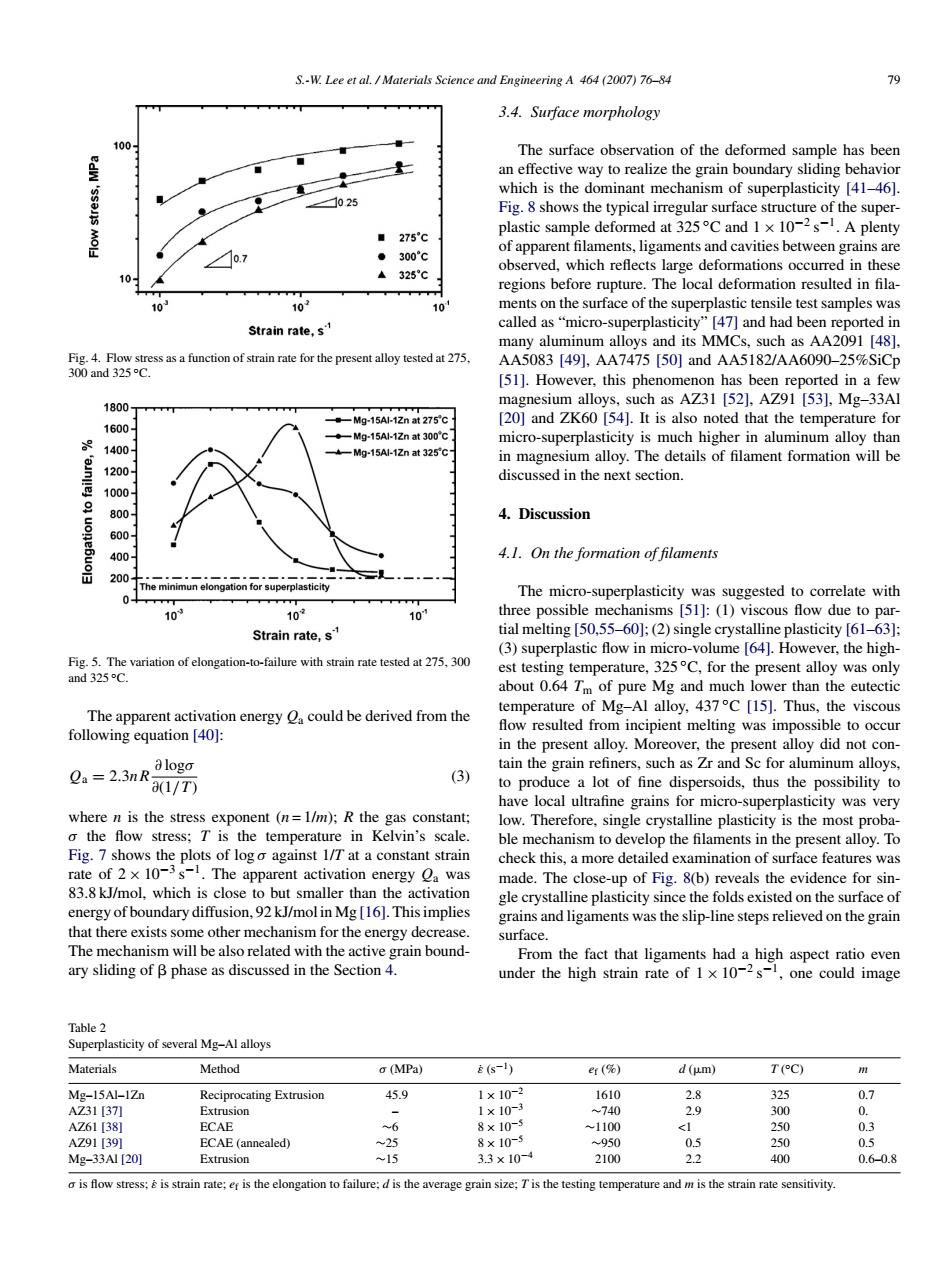
S.-W.Lee et al.Materials Science and Engineering A 464 (2007)76-84 79 3.4.Surface morphology 100 The surface observation of the deformed sample has been an effective way to realize the grain boundary sliding behavior which is the dominant mechanism of superplasticity [41-46]. 0.25 Fig.8 shows the typical irregular surface structure of the super- ■275°c plastic sample deformed at 325C and 1x 10-2s-1.A plenty of apparent filaments,ligaments and cavities between grains are ● 300°c observed,which reflects large deformations occurred in these ▲325°C regions before rupture.The local deformation resulted in fila- 10 10 ments on the surface of the superplastic tensile test samples was Strain rate,s called as"micro-superplasticity"[47]and had been reported in many aluminum alloys and its MMCs,such as AA2091 [48]. Fig.4.Flow stress as a function of strain rate for the present alloy tested at 275 AA5083[491,AA7475[50]and AA5182/AA6090-25%SiCp 300and325C. [51].However,this phenomenon has been reported in a few 1800 magnesium alloys,such as AZ31 [52].AZ91 [53],Mg-33Al 。-Mg-15A1Znat275C [20]and ZK60 [54].It is also noted that the temperature for 1600 ◆-Mg-15A1-1Znat300c micro-superplasticity is much higher in aluminum alloy than 1400 Mg-15Al-1Zn at 325'C in magnesium alloy.The details of filament formation will be 1200 discussed in the next section. 1000 800 4.Discussion 600 400 4.1.On the formation of filaments 200 The minimun elongation for superplasticity 0 The micro-superplasticity was suggested to correlate with 10 102 10 three possible mechanisms [51]:(1)viscous flow due to par- Strain rate,s tial melting [50,55-60]:(2)single crystalline plasticity [61-63]: (3)superplastic flow in micro-volume [64].However,the high- Fig.5.The variation of elongation-to-failure with strain rate tested at 275,300 est testing temperature,325C,for the present alloy was only and 325C. about 0.64 Tm of pure Mg and much lower than the eutectic The apparent activation energy a could be derived from the temperature of Mg-Al alloy,437C [15].Thus,the viscous following equation [40]: flow resulted from incipient melting was impossible to occur in the present alloy.Moreover,the present alloy did not con- alogo tain the grain refiners,such as Zr and Sc for aluminum alloys, Qa=2.3nR a(1/T) (3) to produce a lot of fine dispersoids,thus the possibility to have local ultrafine grains for micro-superplasticity was very where n is the stress exponent (n=1/m);R the gas constant; low.Therefore,single crystalline plasticity is the most proba- o the flow stress;T is the temperature in Kelvin's scale. ble mechanism to develop the filaments in the present alloy.To Fig.7 shows the plots of logo against 1/T at a constant strain check this,a more detailed examination of surface features was rate of 2x 10-3s-1.The apparent activation energy a was made.The close-up of Fig.8(b)reveals the evidence for sin- 83.8 kJ/mol.which is close to but smaller than the activation gle crystalline plasticity since the folds existed on the surface of energy of boundary diffusion,92 kJ/mol in Mg[16].This implies grains and ligaments was the slip-line steps relieved on the grain that there exists some other mechanism for the energy decrease surface. The mechanism will be also related with the active grain bound- From the fact that ligaments had a high aspect ratio even ary sliding of B phase as discussed in the Section 4. under the high strain rate of 1x 10-2s-1,one could image Table 2 Superplasticity of several Mg-Al alloys Materials Method o(MPa) (s-1) e(%) d(pm) T(C) Mg-15Al-1Zn Reciprocating Extrusion 45.9 1×10-2 1610 2.8 325 0.7 AZ31[37J Extrusion 1×10-3 740 2.9 300 0. AZ61[381 ECAE ~6 8×10-5 ~1100 1 250 0.3 AZ91[39] ECAE(annealed) 25 8×10-5 950 0.5 250 0.5 Mg-33A1[20] Extrusion ~15 33×10-4 2100 2.2 400 0.6-0.8 o is flow stress:is strain rate;er is the elongation to failure:d is the average grain size;T is the testing temperature and m is the strain rate sensitivity.S.-W. Lee et al. / Materials Science and Engineering A 464 (2007) 76–84 79 Fig. 4. Flow stress as a function of strain rate for the present alloy tested at 275, 300 and 325 ◦C. Fig. 5. The variation of elongation-to-failure with strain rate tested at 275, 300 and 325 ◦C. The apparent activation energy Qa could be derived from the following equation [40]: Qa = 2.3nR ∂ logσ ∂(1/T ) (3) where n is the stress exponent (n = 1/m); R the gas constant; σ the flow stress; T is the temperature in Kelvin’s scale. Fig. 7 shows the plots of log σ against 1/T at a constant strain rate of 2 × 10−3 s−1. The apparent activation energy Qa was 83.8 kJ/mol, which is close to but smaller than the activation energy of boundary diffusion, 92 kJ/mol in Mg [16]. This implies that there exists some other mechanism for the energy decrease. The mechanism will be also related with the active grain bound￾ary sliding of phase as discussed in the Section 4. 3.4. Surface morphology The surface observation of the deformed sample has been an effective way to realize the grain boundary sliding behavior which is the dominant mechanism of superplasticity [41–46]. Fig. 8 shows the typical irregular surface structure of the super￾plastic sample deformed at 325 ◦C and 1 × 10−2 s−1. A plenty of apparent filaments, ligaments and cavities between grains are observed, which reflects large deformations occurred in these regions before rupture. The local deformation resulted in fila￾ments on the surface of the superplastic tensile test samples was called as “micro-superplasticity” [47] and had been reported in many aluminum alloys and its MMCs, such as AA2091 [48], AA5083 [49], AA7475 [50] and AA5182/AA6090–25%SiCp [51]. However, this phenomenon has been reported in a few magnesium alloys, such as AZ31 [52], AZ91 [53], Mg–33Al [20] and ZK60 [54]. It is also noted that the temperature for micro-superplasticity is much higher in aluminum alloy than in magnesium alloy. The details of filament formation will be discussed in the next section. 4. Discussion 4.1. On the formation of filaments The micro-superplasticity was suggested to correlate with three possible mechanisms [51]: (1) viscous flow due to par￾tial melting [50,55–60]; (2) single crystalline plasticity [61–63]; (3) superplastic flow in micro-volume [64]. However, the high￾est testing temperature, 325 ◦C, for the present alloy was only about 0.64 Tm of pure Mg and much lower than the eutectic temperature of Mg–Al alloy, 437 ◦C [15]. Thus, the viscous flow resulted from incipient melting was impossible to occur in the present alloy. Moreover, the present alloy did not con￾tain the grain refiners, such as Zr and Sc for aluminum alloys, to produce a lot of fine dispersoids, thus the possibility to have local ultrafine grains for micro-superplasticity was very low. Therefore, single crystalline plasticity is the most proba￾ble mechanism to develop the filaments in the present alloy. To check this, a more detailed examination of surface features was made. The close-up of Fig. 8(b) reveals the evidence for sin￾gle crystalline plasticity since the folds existed on the surface of grains and ligaments was the slip-line steps relieved on the grain surface. From the fact that ligaments had a high aspect ratio even under the high strain rate of 1 × 10−2 s−1, one could image Table 2 Superplasticity of several Mg–Al alloys Materials Method σ (MPa) ε˙ (s−1) ef (%) d (m) T ( ◦C) m Mg–15Al–1Zn Reciprocating Extrusion 45.9 1 × 10−2 1610 2.8 325 0.7 AZ31 [37] Extrusion – 1 × 10−3 ∼740 2.9 300 0. AZ61 [38] ECAE ∼6 8 × 10−5 ∼1100 <1 250 0.3 AZ91 [39] ECAE (annealed) ∼25 8 × 10−5 ∼950 0.5 250 0.5 Mg–33Al [20] Extrusion ∼15 3.3 × 10−4 2100 2.2 400 0.6–0.8 σ is flow stress; ε˙ is strain rate; ef is the elongation to failure; d is the average grain size; T is the testing temperature and m is the strain rate sensitivity.