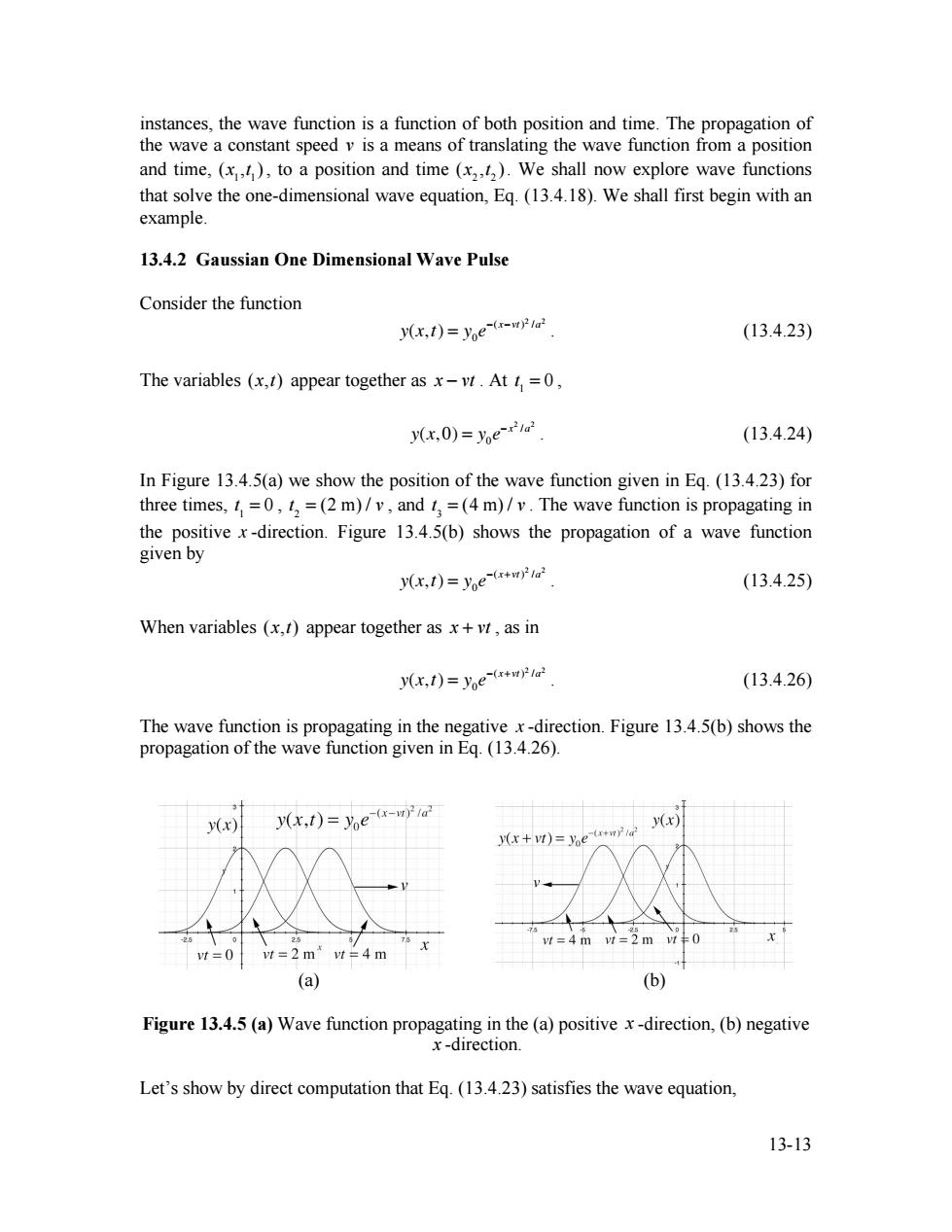
instances,the wave function is a function of both position and time.The propagation of the wave a constant speed v is a means of translating the wave function from a position and time,(x,),to a position and time (x2).We shall now explore wave functions that solve the one-dimensional wave equation,Eq.(13.4.18).We shall first begin with an example. 13.4.2 Gaussian One Dimensional Wave Pulse Consider the function y(x,t)=yoe-(-l (13.4.23) The variables (x,t)appear together as x-vt.At =0, y(x,0)=ye- (13.4.24) In Figure 13.4.5(a)we show the position of the wave function given in Eq.(13.4.23)for three times,=0,=(2 m)/v,and=(4 m)/v.The wave function is propagating in the positive x-direction.Figure 13.4.5(b)shows the propagation of a wave function given by y(x,t)=yoe-(l (13.4.25) When variables (x,t)appear together as x+vt,as in y(x,t)=yoe-(xtwl (13.4.26) The wave function is propagating in the negative x-direction.Figure 13.4.5(b)shows the propagation of the wave function given in Eq.(13.4.26). yx） y(x,t)=ye-(x-mi x+m)）=%e*w广 vt=4 m vt=2m vt vt=2m vt=4 m (a) (b) Figure 13.4.5 (a)Wave function propagating in the (a)positive x-direction,(b)negative x-direction. Let's show by direct computation that Eq.(13.4.23)satisfies the wave equation, 13-1313-13 instances, the wave function is a function of both position and time. The propagation of the wave a constant speed v is a means of translating the wave function from a position and time, (x1,t 1), to a position and time (x2 ,t 2 ). We shall now explore wave functions that solve the one-dimensional wave equation, Eq. (13.4.18). We shall first begin with an example. 13.4.2 Gaussian One Dimensional Wave Pulse Consider the function y(x,t) = y0e!(x!vt) 2 /a2 . (13.4.23) The variables (x,t) appear together as x ! vt . At t 1 = 0 , y(x,0) = y0e! x2 /a2 . (13.4.24) In Figure 13.4.5(a) we show the position of the wave function given in Eq. (13.4.23) for three times, t 1 = 0 , t 2 = (2 m) / v , and t 3 = (4 m) / v . The wave function is propagating in the positive x -direction. Figure 13.4.5(b) shows the propagation of a wave function given by y(x,t) = y0e!(x+vt) 2 /a2 . (13.4.25) When variables (x,t) appear together as x + vt , as in y(x,t) = y0e!(x+vt) 2 /a2 . (13.4.26) The wave function is propagating in the negative x -direction. Figure 13.4.5(b) shows the propagation of the wave function given in Eq. (13.4.26). (a) (b) Figure 13.4.5 (a) Wave function propagating in the (a) positive x -direction, (b) negative x -direction. Let’s show by direct computation that Eq. (13.4.23) satisfies the wave equation