正在加载图片...
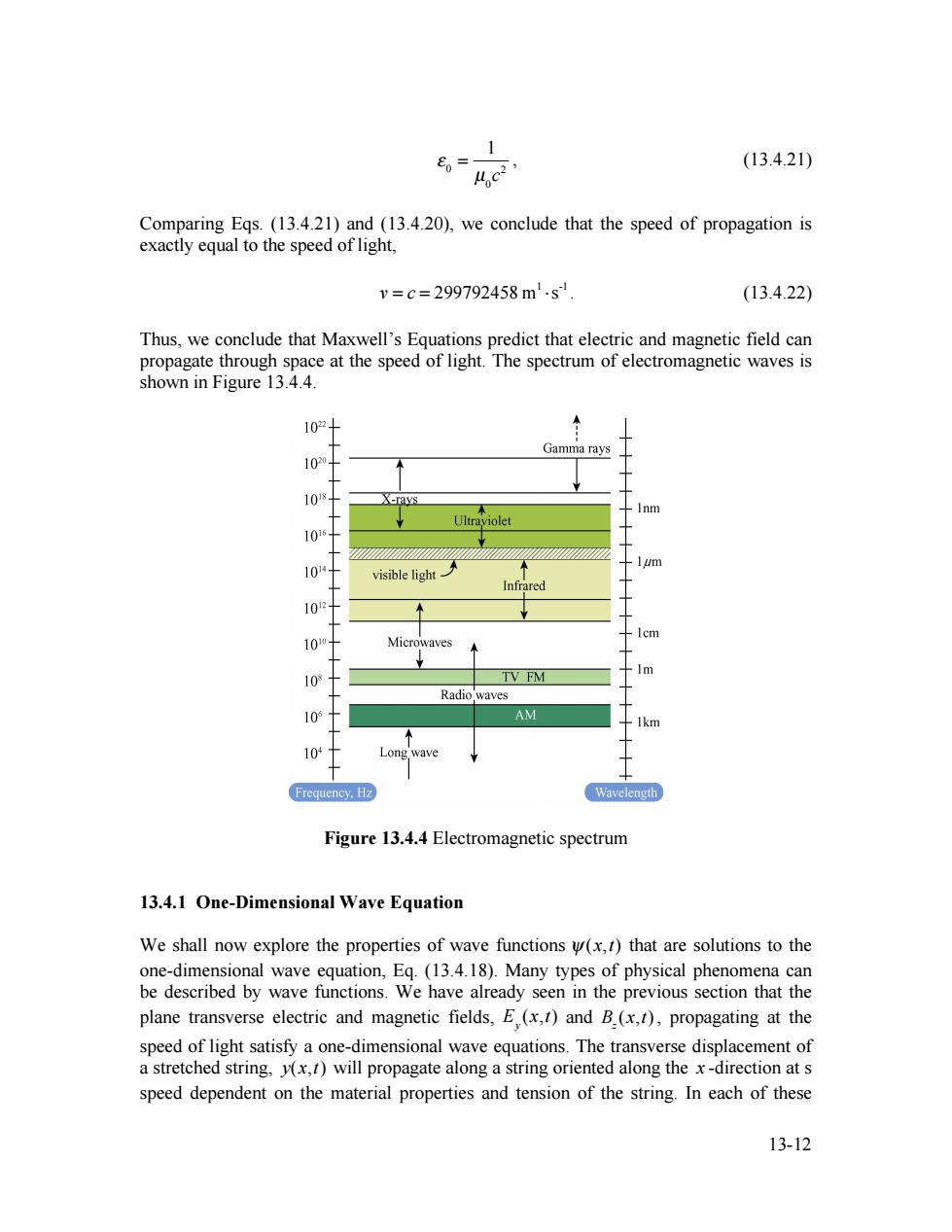
6、1 %c3, (13.4.21) Comparing Eqs.(13.4.21)and (13.4.20),we conclude that the speed of propagation is exactly equal to the speed of light, v=c=299792458m.s (13.4.22) Thus,we conclude that Maxwell's Equations predict that electric and magnetic field can propagate through space at the speed of light.The spectrum of electromagnetic waves is shown in Figure 13.4.4. 1022 Gamma rays 10 108 X-ravs Inm Ultraviolet 1016 visble light入 m 101 Infrared 1012 1cm 1010 Microwaves 10 TV FM Radiowaves 10 AM 1km 104 Long wave Frequency.Hz Wavelength Figure 13.4.4 Electromagnetic spectrum 13.4.1 One-Dimensional Wave Equation We shall now explore the properties of wave functions u(x,t)that are solutions to the one-dimensional wave equation,Eq.(13.4.18).Many types of physical phenomena can be described by wave functions.We have already seen in the previous section that the plane transverse electric and magnetic fields,E(x,t)and B.(x,t),propagating at the speed of light satisfy a one-dimensional wave equations.The transverse displacement of a stretched string,y(x,t)will propagate along a string oriented along the x-direction at s speed dependent on the material properties and tension of the string.In each of these 13-1213-12 ! 0 = 1 µ0 c 2 , (13.4.21) Comparing Eqs. (13.4.21) and (13.4.20), we conclude that the speed of propagation is exactly equal to the speed of light, v = c = 299792458 m1 !s -1 . (13.4.22) Thus, we conclude that Maxwell’s Equations predict that electric and magnetic field can propagate through space at the speed of light. The spectrum of electromagnetic waves is shown in Figure 13.4.4. Figure 13.4.4 Electromagnetic spectrum 13.4.1 One-Dimensional Wave Equation We shall now explore the properties of wave functions ! (x,t) that are solutions to the one-dimensional wave equation, Eq. (13.4.18). Many types of physical phenomena can be described by wave functions. We have already seen in the previous section that the plane transverse electric and magnetic fields, E y (x,t) and Bz (x,t), propagating at the speed of light satisfy a one-dimensional wave equations. The transverse displacement of a stretched string, y(x,t) will propagate along a string oriented along the x -direction at s speed dependent on the material properties and tension of the string. In each of these