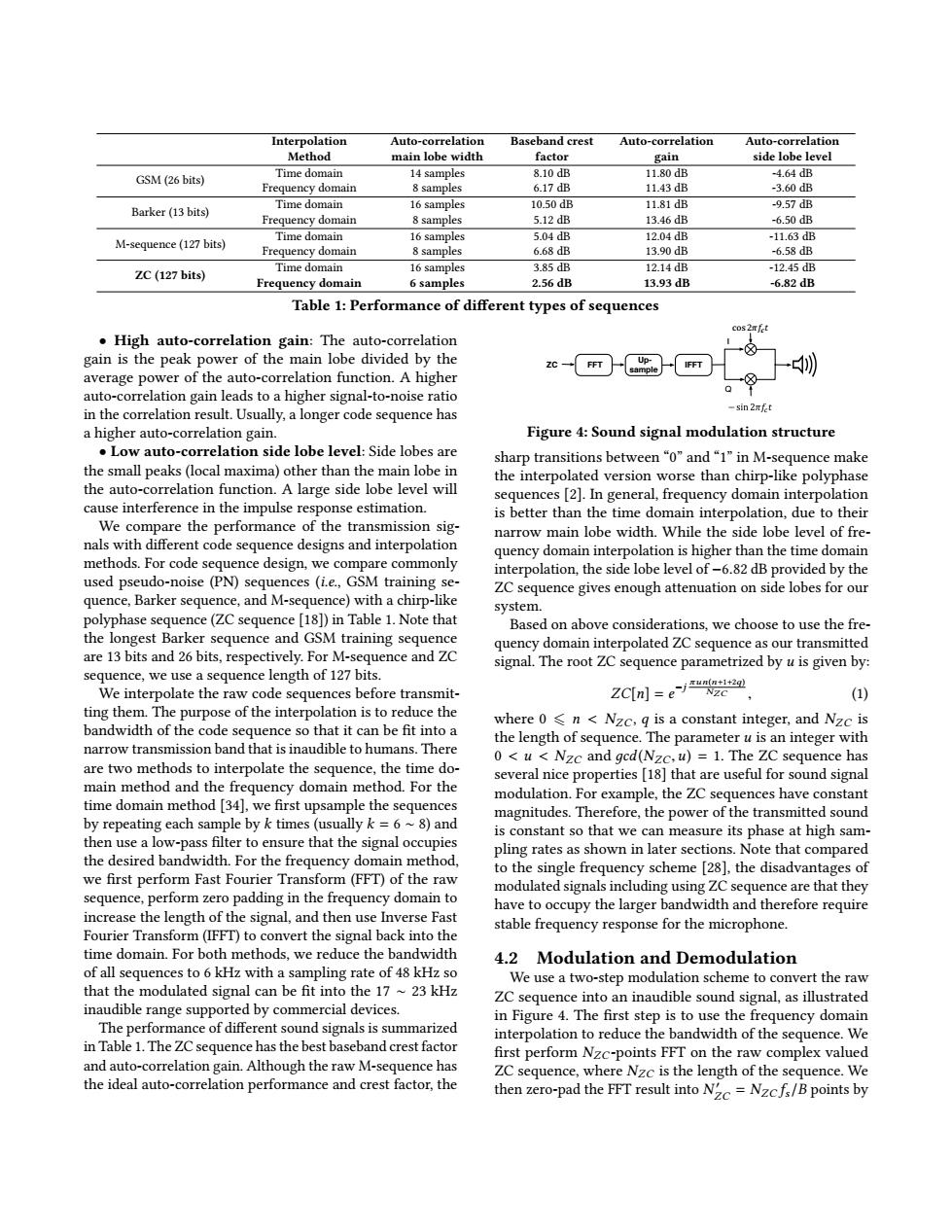
Interpolation Auto-correlation Baseband crest Auto-correlation Auto-correlation Method main lobe width factor gain side lobe level Time domain 14 samples 8.10dB 11.80dB -4.64dB GSM(26 bits) Frequency domain 8 samples 6.17dB 11.43dB -3.60dB Time domain 10.50dB 11.81dB -9.57dB Barker(13 bits) 16 samples Frequency domain 8 samples 5.12dB 13.46dB -6.50dB Time domain 16 samples 5.04dB 12.04dB -11.63dB M-sequence(127 bits) Frequency domain 8 samples 6.68dB 13.90dB -6.58dB Time domain 16 samples 3.85dB 12.14dB -12.45dB ZC(127 bits) Frequency domain 6 samples 2.56dB 13.93dB -6.82dB Table 1:Performance of different types of sequences cos2nfet High auto-correlation gain:The auto-correlation gain is the peak power of the main lobe divided by the FFT Up- sample average power of the auto-correlation function.A higher auto-correlation gain leads to a higher signal-to-noise ratio in the correlation result.Usually,a longer code sequence has -sin 2nfet a higher auto-correlation gain. Figure 4:Sound signal modulation structure Low auto-correlation side lobe level:Side lobes are sharp transitions between "0"and"1"in M-sequence make the small peaks(local maxima)other than the main lobe in the interpolated version worse than chirp-like polyphase the auto-correlation function.A large side lobe level will sequences [2].In general,frequency domain interpolation cause interference in the impulse response estimation. is better than the time domain interpolation,due to their We compare the performance of the transmission sig- narrow main lobe width.While the side lobe level of fre- nals with different code sequence designs and interpolation quency domain interpolation is higher than the time domain methods.For code sequence design,we compare commonly interpolation,the side lobe level of-6.82 dB provided by the used pseudo-noise (PN)sequences (i.e,GSM training se- ZC sequence gives enough attenuation on side lobes for our quence,Barker sequence,and M-sequence)with a chirp-like system. polyphase sequence(ZC sequence [18])in Table 1.Note that Based on above considerations,we choose to use the fre- the longest Barker sequence and GSM training sequence quency domain interpolated ZC sequence as our transmitted are 13 bits and 26 bits,respectively.For M-sequence and ZC signal.The root ZC sequence parametrized by u is given by: sequence,we use a sequence length of 127 bits. We interpolate the raw code sequences before transmit- ZC[n川=ej“g2 (1) ting them.The purpose of the interpolation is to reduce the bandwidth of the code sequence so that it can be fit into a where 0 s n Nzc,q is a constant integer,and Nzc is the length of sequence.The parameter u is an integer with narrow transmission band that is inaudible to humans.There 0<u Nzc and gcd(Nzc,u)=1.The ZC sequence has are two methods to interpolate the sequence,the time do- several nice properties [18]that are useful for sound signal main method and the frequency domain method.For the modulation.For example,the ZC sequences have constant time domain method [34],we first upsample the sequences magnitudes.Therefore,the power of the transmitted sound by repeating each sample by k times(usually k=6~8)and is constant so that we can measure its phase at high sam- then use a low-pass filter to ensure that the signal occupies pling rates as shown in later sections.Note that compared the desired bandwidth.For the frequency domain method, to the single frequency scheme [28],the disadvantages of we first perform Fast Fourier Transform(FFT)of the raw modulated signals including using ZC sequence are that they sequence,perform zero padding in the frequency domain to have to occupy the larger bandwidth and therefore require increase the length of the signal,and then use Inverse Fast stable frequency response for the microphone. Fourier Transform(IFFT)to convert the signal back into the time domain.For both methods,we reduce the bandwidth 4.2 Modulation and Demodulation of all sequences to 6 kHz with a sampling rate of 48 kHz so We use a two-step modulation scheme to convert the raw that the modulated signal can be fit into the 17~23 kHz ZC sequence into an inaudible sound signal,as illustrated inaudible range supported by commercial devices. in Figure 4.The first step is to use the frequency domain The performance of different sound signals is summarized interpolation to reduce the bandwidth of the sequence.We in Table 1.The ZC sequence has the best baseband crest factor first perform Nzc-points FFT on the raw complex valued and auto-correlation gain.Although the raw M-sequence has ZC sequence,where Nzc is the length of the sequence.We the ideal auto-correlation performance and crest factor,the then zero-pad the FFT result into Nc=Nzcfs/B points byInterpolation Method Auto-correlation main lobe width Baseband crest factor Auto-correlation gain Auto-correlation side lobe level GSM (26 bits) Time domain 14 samples 8.10 dB 11.80 dB -4.64 dB Frequency domain 8 samples 6.17 dB 11.43 dB -3.60 dB Barker (13 bits) Time domain 16 samples 10.50 dB 11.81 dB -9.57 dB Frequency domain 8 samples 5.12 dB 13.46 dB -6.50 dB M-sequence (127 bits) Time domain 16 samples 5.04 dB 12.04 dB -11.63 dB Frequency domain 8 samples 6.68 dB 13.90 dB -6.58 dB ZC (127 bits) Time domain 16 samples 3.85 dB 12.14 dB -12.45 dB Frequency domain 6 samples 2.56 dB 13.93 dB -6.82 dB Table 1: Performance of different types of sequences • High auto-correlation gain: The auto-correlation gain is the peak power of the main lobe divided by the average power of the auto-correlation function. A higher auto-correlation gain leads to a higher signal-to-noise ratio in the correlation result. Usually, a longer code sequence has a higher auto-correlation gain. • Low auto-correlation side lobe level: Side lobes are the small peaks (local maxima) other than the main lobe in the auto-correlation function. A large side lobe level will cause interference in the impulse response estimation. We compare the performance of the transmission sig￾nals with different code sequence designs and interpolation methods. For code sequence design, we compare commonly used pseudo-noise (PN) sequences (i.e., GSM training se￾quence, Barker sequence, and M-sequence) with a chirp-like polyphase sequence (ZC sequence [18]) in Table 1. Note that the longest Barker sequence and GSM training sequence are 13 bits and 26 bits, respectively. For M-sequence and ZC sequence, we use a sequence length of 127 bits. We interpolate the raw code sequences before transmit￾ting them. The purpose of the interpolation is to reduce the bandwidth of the code sequence so that it can be fit into a narrow transmission band that is inaudible to humans. There are two methods to interpolate the sequence, the time do￾main method and the frequency domain method. For the time domain method [34], we first upsample the sequences by repeating each sample by k times (usually k = 6 ∼ 8) and then use a low-pass filter to ensure that the signal occupies the desired bandwidth. For the frequency domain method, we first perform Fast Fourier Transform (FFT) of the raw sequence, perform zero padding in the frequency domain to increase the length of the signal, and then use Inverse Fast Fourier Transform (IFFT) to convert the signal back into the time domain. For both methods, we reduce the bandwidth of all sequences to 6 kHz with a sampling rate of 48 kHz so that the modulated signal can be fit into the 17 ∼ 23 kHz inaudible range supported by commercial devices. The performance of different sound signals is summarized in Table 1. The ZC sequence has the best baseband crest factor and auto-correlation gain. Although the raw M-sequence has the ideal auto-correlation performance and crest factor, the ZC IFFT Up￾sample I Q

 FFT Figure 4: Sound signal modulation structure sharp transitions between “0” and “1” in M-sequence make the interpolated version worse than chirp-like polyphase sequences [2]. In general, frequency domain interpolation is better than the time domain interpolation, due to their narrow main lobe width. While the side lobe level of fre￾quency domain interpolation is higher than the time domain interpolation, the side lobe level of −6.82 dB provided by the ZC sequence gives enough attenuation on side lobes for our system. Based on above considerations, we choose to use the fre￾quency domain interpolated ZC sequence as our transmitted signal. The root ZC sequence parametrized by u is given by: ZC[n] = e −j πun(n+1+2q) NZC , (1) where 0 ⩽ n < NZC, q is a constant integer, and NZC is the length of sequence. The parameter u is an integer with 0 < u < NZC and дcd(NZC,u) = 1. The ZC sequence has several nice properties [18] that are useful for sound signal modulation. For example, the ZC sequences have constant magnitudes. Therefore, the power of the transmitted sound is constant so that we can measure its phase at high sam￾pling rates as shown in later sections. Note that compared to the single frequency scheme [28], the disadvantages of modulated signals including using ZC sequence are that they have to occupy the larger bandwidth and therefore require stable frequency response for the microphone. 4.2 Modulation and Demodulation We use a two-step modulation scheme to convert the raw ZC sequence into an inaudible sound signal, as illustrated in Figure 4. The first step is to use the frequency domain interpolation to reduce the bandwidth of the sequence. We first perform NZC-points FFT on the raw complex valued ZC sequence, where NZC is the length of the sequence. We then zero-pad the FFT result into N ′ ZC = NZC fs /B points by