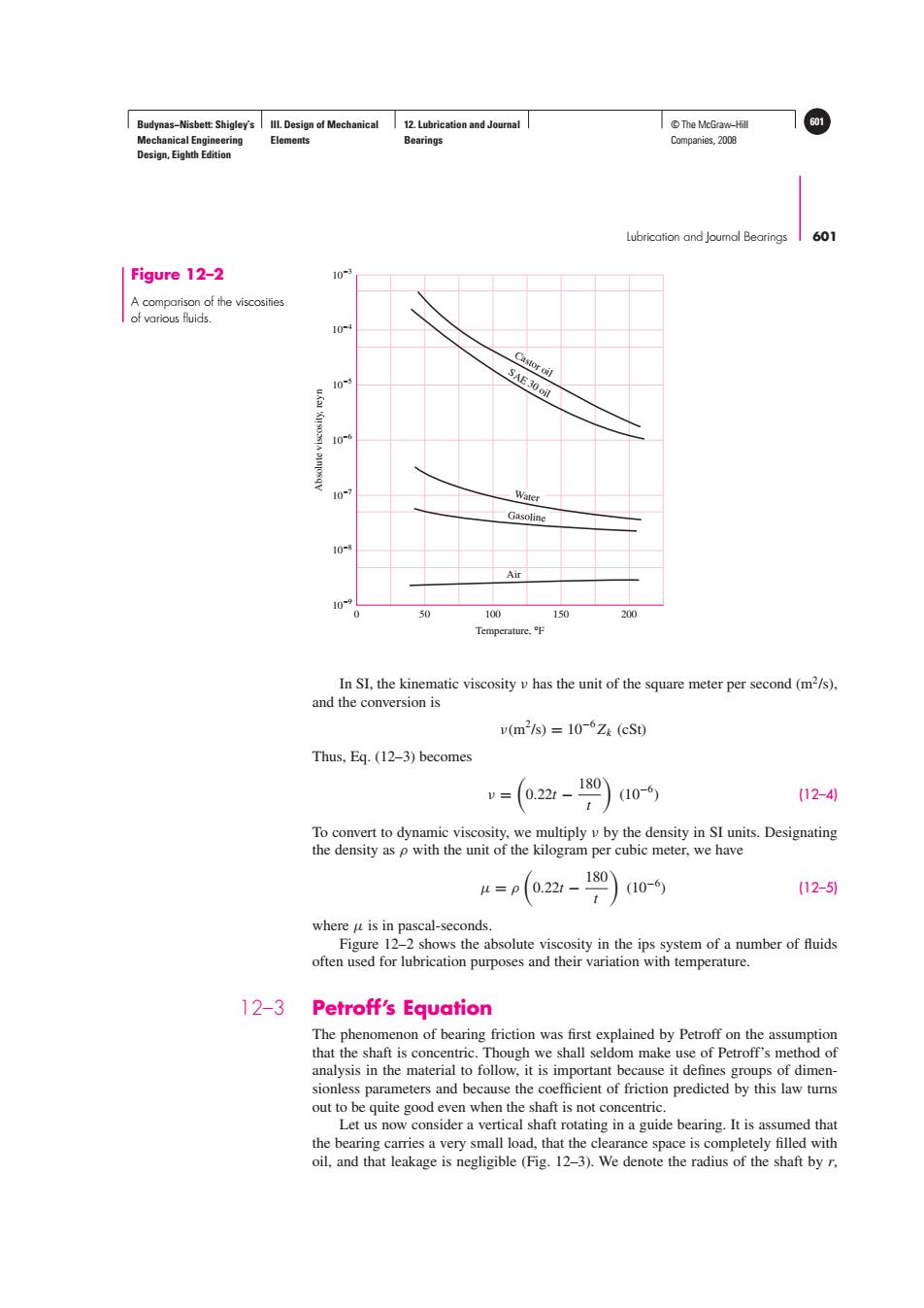
Budynas-Nisbett:Shigley's Ill.Design of Mechanical 12.Lubrication and Journal T©The McGraw-Hil 601 Mechanical Engineering Elements Bearings Companies,2008 Design,Eighth Edition Lubrication and Joumnal Bearings 601 Figure 12-2 10- A comparison of the viscosities of various fluids. 104 Castor oil 10s SAE30 oil 106 0 Water Gasoline 10- Air 50 100 150 200 Temperature,F In SI,the kinematic viscosity v has the unit of the square meter per second(m2/s). and the conversion is v(m2s)=10-6Zk(cS0) Thus,Eq.(12-3)becomes =(2-g9 (10-6) (12-4 To convert to dynamic viscosity,we multiply v by the density in SI units.Designating the density as p with the unit of the kilogram per cubic meter,we have u=p0.22t- 180 (10-6) (12-5) where u is in pascal-seconds. Figure 12-2 shows the absolute viscosity in the ips system of a number of fluids often used for lubrication purposes and their variation with temperature. 12-3 Petroff's Equation The phenomenon of bearing friction was first explained by Petroff on the assumption that the shaft is concentric.Though we shall seldom make use of Petroff's method of analysis in the material to follow,it is important because it defines groups of dimen- sionless parameters and because the coefficient of friction predicted by this law turns out to be quite good even when the shaft is not concentric. Let us now consider a vertical shaft rotating in a guide bearing.It is assumed that the bearing carries a very small load,that the clearance space is completely filled with oil,and that leakage is negligible (Fig.12-3).We denote the radius of the shaft by r.Budynas−Nisbett: Shigley’s Mechanical Engineering Design, Eighth Edition III. Design of Mechanical Elements 12. Lubrication and Journal Bearings © The McGraw−Hill 601 Companies, 2008 Lubrication and Journal Bearings 601 Figure 12–2 A comparison of the viscosities of various fluids. Air 0 50 100 150 200 10−9 10−8 10−7 10−6 10−5 10−4 10−3 Temperature, °F Absolute viscosity, reyn Castor oi SA l E 30 oil Water Gasoline In SI, the kinematic viscosity ν has the unit of the square meter per second (m2/s), and the conversion is ν(m2 /s) = 10−6Zk (cSt) Thus, Eq. (12–3) becomes ν = 0.22t − 180 t (10−6 ) (12–4) To convert to dynamic viscosity, we multiply ν by the density in SI units. Designating the density as ρ with the unit of the kilogram per cubic meter, we have μ = ρ 0.22t − 180 t (10−6 ) (12–5) where μ is in pascal-seconds. Figure 12–2 shows the absolute viscosity in the ips system of a number of fluids often used for lubrication purposes and their variation with temperature. 12–3 Petroff’s Equation The phenomenon of bearing friction was first explained by Petroff on the assumption that the shaft is concentric. Though we shall seldom make use of Petroff’s method of analysis in the material to follow, it is important because it defines groups of dimen￾sionless parameters and because the coefficient of friction predicted by this law turns out to be quite good even when the shaft is not concentric. Let us now consider a vertical shaft rotating in a guide bearing. It is assumed that the bearing carries a very small load, that the clearance space is completely filled with oil, and that leakage is negligible (Fig. 12–3). We denote the radius of the shaft by r,