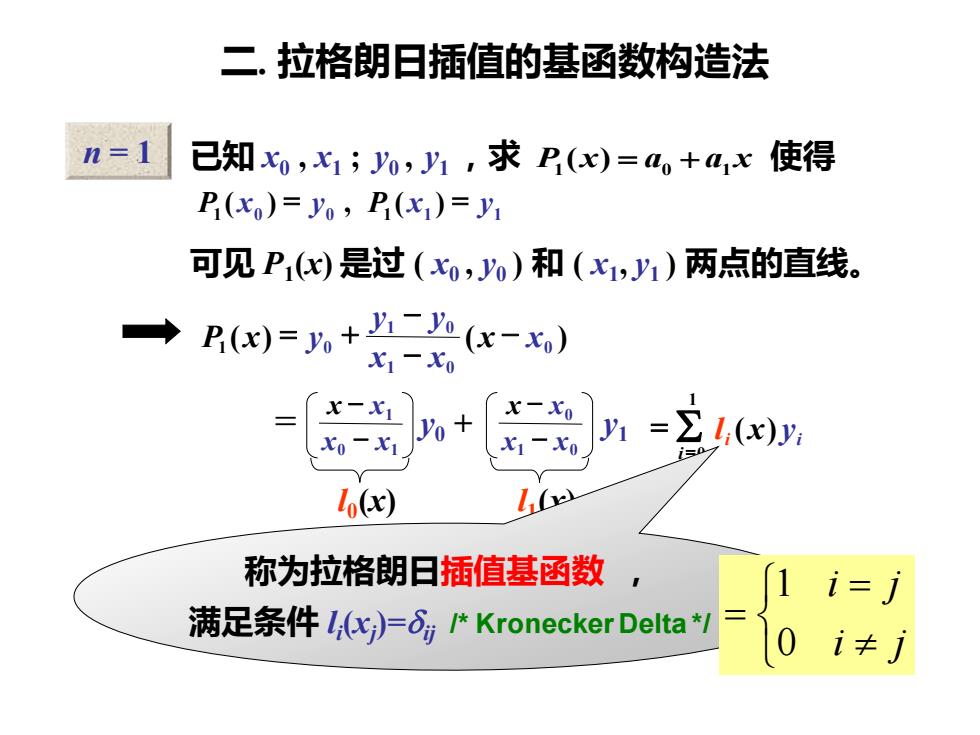
二.拉格朗日插值的基函数构造法 n=】 已知x0,x1;0,y1,求P()=+a,x使得 P(x)=y,P(x1)=y1 可见P)是过(0,0)和(x1,y1)两点的直线。 Px)=+二(x-x) X1一X0 x-y%+ x-Xo 1-x0 ()y 0 1(x) lx 称为拉格朗日插值基函数 i=i 满足条件l,c)=可Kronecker Delta i≠ n = 1 已知 x0 , x1 ; y0 , y1 ，求 P1 (x) = a0 + a1 x 使得 1 0 0 1 1 1 P ( x ) = y , P ( x ) = y 可见 P1 (x) 是过 ( x0 , y0 ) 和 ( x1 , y1 ) 两点的直线。 ( ) ( ) 0 1 0 1 0 1 0 x x x x y y P x y − − − = + 0 1 1 x x x x − − 1 0 0 x x x x − − = y0 + y1 l0 (x) l1 (x) = = 1 0 ( ) i i x yi l 称为拉格朗日插值基函数 ， 满足条件 l i (xj )=ij /* Kronecker Delta */ 二. 拉格朗日插值的基函数构造法     = = i j i j 0 1