
数据插值 ·多项式插值问题的一般提法 ·插值多项式的唯一性 拉格朗日插值的基函数构造法 ·插值余项 ·分段插值
数据插值 • 多项式插值问题的一般提法 • 插值多项式的唯一性 • 拉格朗日插值的基函数构造法 • 插值余项 • 分段插值

数据插值 。 多项式插值问题的一般提法 ·插值多项式的唯一性 ·拉格朗日插值的基函数构造法 ·插值余项 ·分段插值
数据插值 • 多项式插值问题的一般提法 • 插值多项式的唯一性 • 拉格朗日插值的基函数构造法 • 插值余项 • 分段插值

以近似计算函数值为例来说明 例:设在实际问题中,某些变量之间的函 数关系是存在的,但通常不能用式子表示 只能由实验、观测得到y=f(x)在一系列离 散点上的函数值,即已知函数表 X Xo 双(化*,≠) yo y1
以近似计算函数值为例来说明 散点上的函数值,即已知函数表 例:设在实际问题中,某些变量之间的函 数关系是存在的,但通常不能用式子表示, 只能由实验、观测得到 y f x = ( ) 在一系列离 x y x0 1 xn x y0 y1 yn ( x x i j i j , )

如何计算f(x)(c≠x,i=0,1,n)?我们希望 寻求一个简单且易于计算的函数P(x)来近 似f(x),即f(x)≈P(x),一般P(x)可选为多 多项式、三角多项式、有理函数或样条函数 等。 有些函数虽有表达式,但较复杂,计算函数 值不经济,这时也希望用简单的函数来逼近
如何计算 f x( ) ( x x i n = i , , , , 0 1 ) ?我们希望 寻求一个简单且易于计算的函数 P x( ) 来近 似 f x( ) ,即 f x P x ( ) ( ) ,一般 P x( ) 可选为多 多项式、三角多项式、有理函数或样条函数 等。 有些函数虽有表达式,但较复杂,计算函数 值不经济,这时也希望用简单的函数来逼近
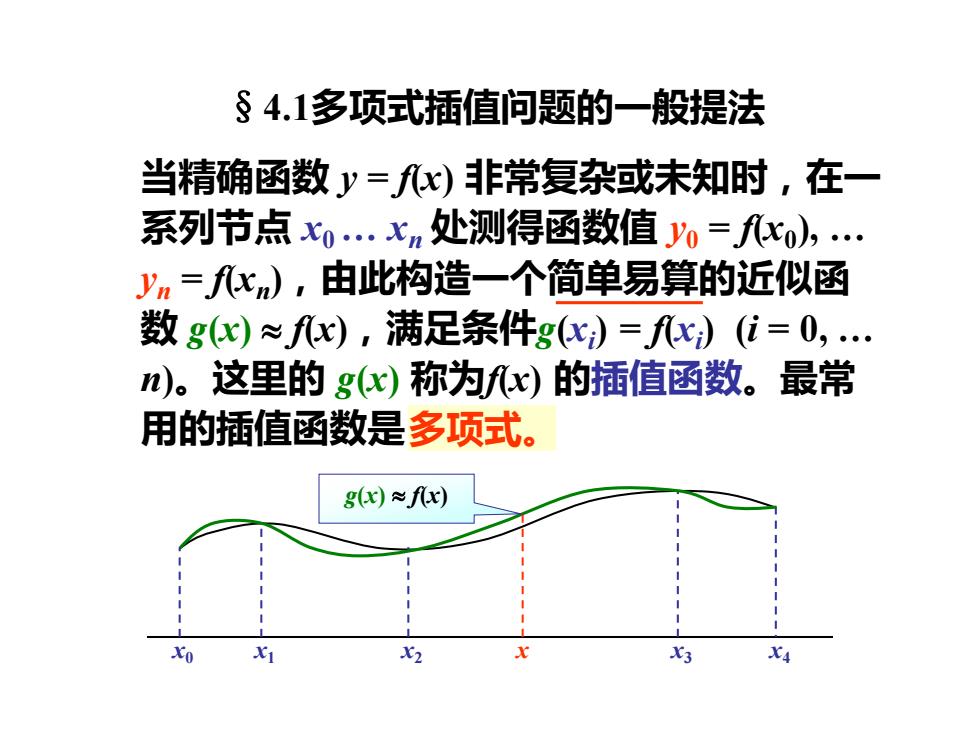
§4.1多项式插值问题的一般提法 当精确函数y=x)非常复杂或未知时,在一 系列节点x.xn处测得函数值0=fx),. yn=c),由此构造一个简单易算的近似函 数g)≈f),满足条件gc)=f)(位=0,. n)。这里的gc)称为fx)的插值函数。最常 用的插值函数是多项式。 gc)≈f) Xo X X3 X
当精确函数 y = f(x) 非常复杂或未知时,在一 系列节点 x0 . xn 处测得函数值 y0 = f(x0 ), . yn = f(xn ),由此构造一个简单易算的近似函 数 g(x) f(x),满足条件g(xi ) = f(xi ) (i = 0, . n)。这里的 g(x) 称为f(x) 的插值函数。最常 用的插值函数是多项式。 .? x0 x1 x2 x x3 x4 g(x) f(x) §4.1多项式插值问题的一般提法

数据插值 多项式插值问题的一般提法 ·插值多项式的唯一性 ·拉格朗日插值的基函数构造法 ·插值余项 ·分段插值
数据插值 • 多项式插值问题的一般提法 • 插值多项式的唯一性 • 拉格朗日插值的基函数构造法 • 插值余项 • 分段插值

§4.2拉格朗日(Lagrange)插值 求n次多项式Pn(x)=a,+a,x+.+anx”使得 Pn(x;)=y:,i=0,.,n 条件:无重合节点,即i≠方→x:≠) 一.插值多项式的存在唯一性 定理4.2.1:在n+1个互异节点x.处满足插值条件 Pn(xk)=yk(k=0,1,2,n) 的次数不超过n的多项式Pn(x)存在且唯一。 证明:代入插值条件得: ao axo+.+a=o o+a1X1+.+anx”=y1 ao +axn+.+ax=
§4.2 拉格朗日(Lagrange)插值 Pn ( xi ) = yi , i = 0, . , n 求 n 次多项式 使得 n Pn (x) = a0 + a1 x ++ an x 条件:无重合节点,即 i j xi x j . : 1 ( ) ( 0,1,2,., ) ( ) k n k k n n x P x y k n n P x + = = 一 插值多项式的存在唯一性 在 个互异节点 处满足插值条件 的次数不超过 的多项式 存在且唯一。 定理4.2.10 1 0 0 0 0 1 1 1 1 0 1 : : . . . . n n n n n n n n n a a x a x y a a x a x y a a x a x y + + + = + + + = + + + = 证明 代入插值条件得

系数行列式是Vandermonde行列式: =Π(x,-x)≠0, 0sj<i<n 故由Cramer法则知,该方程组解存在唯一, 即多项式(系数)存在唯一。 注:这样求Lagrange?插值多项式计算量大,不便于实际应用。 一次多项式插值-过两点直线。 二次多项式插值-过三点抛物线。 若不将多项式次数限制为,则插值多项式不唯一
0 0 1 1 0 Vandermonde : 1 1 ( ) 0 1 n n i j j i n n n n x x x x x x x x = − 系数行列式是 行列式 , 注: 这样求Lagrange插值多项式计算量大,不便于实际应用。 一次多项式插值 - 过两点直线。 二次多项式插值 - 过三点抛物线。 若不将多项式次数限制为 n ,则插值多项式不唯一。 ramer ( ) 故由C 即多项式 系数 存在唯一。 法则知,该方程组解存在唯一

数据插值 。 多项式插值问题的一般提法 ·插值多项式的唯一性 。拉格朗日插值的基函数构造法 。插值余项 ·分段插值
数据插值 • 多项式插值问题的一般提法 • 插值多项式的唯一性 • 拉格朗日插值的基函数构造法 • 插值余项 • 分段插值
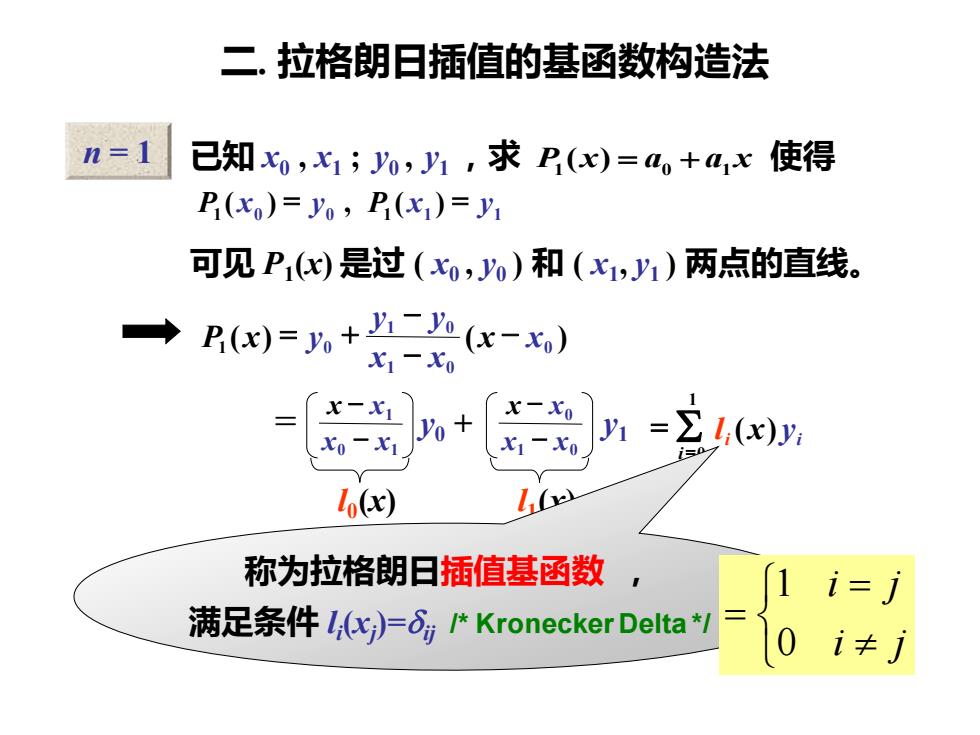
二.拉格朗日插值的基函数构造法 n=】 已知x0,x1;0,y1,求P()=+a,x使得 P(x)=y,P(x1)=y1 可见P)是过(0,0)和(x1,y1)两点的直线。 Px)=+二(x-x) X1一X0 x-y%+ x-Xo 1-x0 ()y 0 1(x) lx 称为拉格朗日插值基函数 i=i 满足条件l,c)=可Kronecker Delta i≠
n = 1 已知 x0 , x1 ; y0 , y1 ,求 P1 (x) = a0 + a1 x 使得 1 0 0 1 1 1 P ( x ) = y , P ( x ) = y 可见 P1 (x) 是过 ( x0 , y0 ) 和 ( x1 , y1 ) 两点的直线。 ( ) ( ) 0 1 0 1 0 1 0 x x x x y y P x y − − − = + 0 1 1 x x x x − − 1 0 0 x x x x − − = y0 + y1 l0 (x) l1 (x) = = 1 0 ( ) i i x yi l 称为拉格朗日插值基函数 , 满足条件 l i (xj )=ij /* Kronecker Delta */ 二. 拉格朗日插值的基函数构造法 = = i j i j 0 1