
第十一章 第三节一所孩性微分方程 (Linear differential equation of first order) 一、 线性微分方程 二、伯努利方程 三、小结与思考练习 2009年7月27日星期一 目录 上页 下页 返回
2009年7月27日星期一 1 目录 上页 下页 返回 第三节 一阶线性微分方程 第十一章 (Linear differential equation of first order) 一、线性微分方程 二、伯努利方程 三、小结与思考练习

一、线性微分方程(Linear differential equation) 形如 y'+p(x)y=g(x) (1) 的方程,称为一阶线性微分方程. 在方程(1)中,若q(x)≠0,则称方程(1)为 一阶非齐次线性微分方程;若q(x)=0,则方程(1)写为 y'+p(x)y=0, (2) 方程(2)称为方程(1)所对应的齐次方程. 注意:这里的“齐次”是指方程(1)的右端为0, 而上一节的“齐次方程”中的“齐次”是指对x与y而言 次数相同.两者含义不同,请勿混淆、 2009年7月27日星期一 2 目录 上页 下页 、返回
2009年7月27日星期一 2 目录 上页 下页 返回 一、线性微分方程 (Linear differential equation) 形如 y′ + p x() () y = q x ( 1 ) 的方程,称为一阶线性微分方程. 在方程( 1)中,若q x() 0 ≠ ,则称方程( 1)为 一 阶非齐次线性微分方程 ; 若 q x() 0 ≡ ,则方程( 1)写为 y pxy ′ + () 0 = , ( 2 ) 方程( 2)称为方程( 1)所对应的齐次方程. 注意:这里的“齐次”是指方程( 1)的右端为 0, 而上一节 的“齐次方程”中的“齐次”是指 对 x 与 y 而言, 次数相同.两者含义不同,请勿混淆.

下面我们来讨论一阶线性微分方程的解法. 首先求方程(1)所对应的齐次方程(2)的通解, 它是可分离变量的方程.分离变量,得 y=-p(x)dx y 两边积分,得通解为 In|y-p(x)dx+InC 或 y=CeJ(C=tC】 (3) 再求一阶非齐次线性微分方程(1),即 y+p(x)y=q(x)(其中q(x)≠0) (4) 的通解. 2009年7月27日星期一 3 目录 上页 下页 返回
2009年7月27日星期一 3 目录 上页 下页 返回 下面我们来讨论一阶线性微分方程的解法. 首先求方程( 1)所对应的齐次方程( 2)的通解, 它是可分离变量的方程.分离变量,得 1 d ( )d y px x y = − 两边积分,得通解为 1 ln | | ( )d ln y px x C =− + ∫ 或 ( )d e p x x y C − ∫ = (C C = ± 1 ). ( 3 ) 再求一阶非齐次线性微分方程( 1 ),即 y pxy qx ′ + = () () (其中 q x() 0 ≠ ) ( 4 ) 的通解.

特方数()变花为些-%个小 两边积分,得nl∫ydx-Jrdx 若记∫dx=),则lny()-∫p)dx g即y=e(x)ep(x)dx=u(x)ep)ax(其中(x)=e)). 将这个解与对应的齐次方程(2)的通解(3)作比较, 易见其表达式形式一致,只需将式(3)中的常数C换成u(x) 由此我们引入求一阶非齐次线性微分方程通解的常数变易 法,即在求出对应齐次方程的通解(3)后,将通解中的常 2009年7月27日星期一 4 目录 上页 下页 返回
2009年7月27日星期一 4 目录 上页 下页 返回 将方程( 4)变形为 d () ()d, y qx px x y y ⎡ ⎤ = − ⎢ ⎥ ⎣ ⎦ 两边积分,得 ( ) ln | | d ( )d , q x y x px x y = − ∫ ∫ 若记 ( ) d () q x x vx y = ∫ ,则ln | | y = − vx px x ( ) ( )d , ∫ 即 ( ) ( )d ( )d e e ( )e vx px x px x y u x − − ∫ ∫ = = (其中 ( ) () ev x u x = ) . 将这个解与对应的齐次方程( 2)的通解( 3)作比较, 易见其表达式形式一致,只需将式( 3)中的常数 C 换成u x( ) . 由此我们引入求一阶非齐次线性微分方程通解的常数变 易 法,即在求出对应齐次方程的通解( 3)后,将通解中的常

数C变易为待定函数(x),并设一阶非齐次线性微分方 程通解为 y=u(x)e (5) 对(5)式两边求导,得 y(eux)p(x)e -u(x)e-p(x)y 代入方程(4),得 u(x) =q(x), (6) 解方程(6),得 4(x)=∫q(x)eJ地dr+C 代入(5)式,得 y=eJau[ωex+C (7) 它即为方程(4)的通解: 2009年7月27日星期一 目录 上页 下页 返回
2009年7月27日星期一 5 目录 上页 下页 返回 数 C 变易为待定函数u x( ) , ( )d ( )e p x x y ux − ∫ = , ( 5 ) 对( 5)式两边求导,得 并设一阶非齐次线性微分方 程通解为 ( )d ( )d ( )e ( ) ( )e p x x px x y u x uxpx − − ∫ ∫ ′ ′ = − ( )d ( )e ( ) px x u x pxy − ∫ = − ′ 代入方程( 4 ),得 ( )d ( )e ( ) 6 px x u x qx − ∫ ′ = , ) ( 解方程( 6 ),得 ( )d ( ) ( )e d px x ux qx x C ∫ = + ∫ 代入( 5)式,得 ( )d ( )d e ( )e d 7 px x px x y qx x C −∫ ∫ ⎡ ⎤ = + ⎢ ⎥ ⎣ ⎦ ∫ ( ) 它即为方程( 4)的通解.
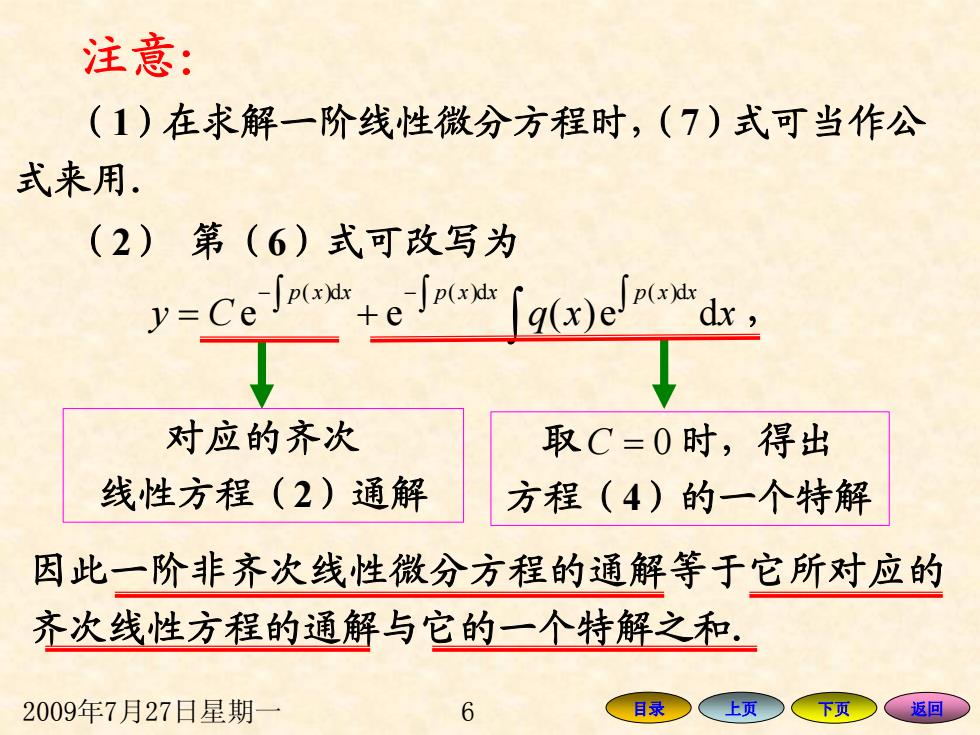
注意: (1)在求解一阶线性微分方程时,(7)式可当作公 式来用. (2)第(6)式可改写为 对应的齐次 取C=0时,得出 线性方程(2)通解 方程(4)的一个特解 因此一阶非齐次线性微分方程的通解等于它所对应的 齐次线性方程的通解与它的一个特解之和, 2009年7月27日星期一 6 目录 上页 下页 返回
2009年7月27日星期一 6 目录 上页 下页 返回 注意: ( 1)在求解一阶线性微分方程时, ( 7 )式可当作公 式来用. ( 2 ) 第( 6)式可改写为 ( )d ( )d ( )d e e ( )e d px x px x px x y C qx x − − ∫∫ ∫ = + ∫ , 对应的齐次 线性方程( 2)通解 取 C = 0 时,得出 方程( 4)的一个特解 因此一阶非齐次线性微分方程的通解等于它所对应 的 齐次线性方程的通解与它的一个特解之和.

例1求微分方程y+y sinx 的通解 X X 解:显然,原方程是一阶非齐次线性方程, 这里p()=1, 9(x)=s nx X 于是,所求通解为 -ef[me+C dx -e{四exc =1(-c0sx+C) X 2009年7月27日星期一 7 目录○ 上页 下页 、返回
2009年7月27日星期一 7 目录 上页 下页 返回 例 1 求微分方程 1 sin x y y x x ′ + = 的通解. 解 :显然,原方程是一阶非齐次线性方程, 这里 1 p x( ) x = , sin ( ) x q x x = . 于是,所求通解为 1 d e x x y − ∫ = 1 in d d s e x x x C x x ⎛ ⎞ ∫ ⎜ ⎟ ⋅ + ⎝ ⎠ ∫ ( )d ( )d e ( )e d px x px x y qx x C −∫ ∫ ⎡ ⎤ = + ⎢ ⎥ ⎣ ⎦ ∫ ln sin ln e ed x x x x C x − ⎛ ⎞ = ⋅+ ⎜ ⎟ ⎝ ⎠ ∫ 1 ( cos ) x C x =− +

5 例2求方程少-2少=x+的通解 dx x+1 解:显然,原方程是一阶非齐次线性方程, 在此,我们不直接套公式,而采用常数变易法来求解 先求对应的齐次方程的通解,由少-2少=0分离变量,得 x+1 两端和分,符时应来次方程的通解为)兮+以,共中 C为任意常数, 再利用常数变易法,设原方程的通解为 y4(xyx+1)2, (8) 2009年7月27日星期一 8 目录○ (上页 下页 、返回
2009年7月27日星期一 8 目录 上页 下页 返回 例 2 求方程 5 2 d 2 ( 1) d 1 y y x x x − =+ + 的通解. 解 :显然,原方程是一阶非齐次线性方程, 在此,我们不直接套公式,而采用常数变易法来求解. 先求对应的齐次方程的通解, 由 d 2 0 d 1 y y x x − = + 分离变量,得 1 2 d d 1 y x y x = + 两端积分,得对应齐次方程的通解为 2 1 y Cx = ( 1) + ,其中 C1 为任意常数. 再利用常数变易法,设原方程的通解为 2 y ux x = ( )( 1) + , ( 8 )

求导,得 =4(x)(x+I2+2u(xx+1) dx 代入原方程,整理得 u'(x)=(x+1)2 两端积分,得 -+)+c 将其代入(8)式,即得到原方程的通解为 =e+a+ 2009年7月27日星期一 9 目录会 上页 下页 返回
2009年7月27日星期一 9 目录 上页 下页 返回 求导,得 d 2 ( )( 1) 2 ( )( 1) d y u x x ux x x = ′ ++ + 代入原方程,整理得 1 2 ux x ′( ) ( 1) = + 两端积分,得 3 2 ( ) 2 ( 1) 3 u x = x + + C 将其代入( 8)式,即得到原方程的通解为 2 3 2 2 ( 1) ( 1) 3 y x x C ⎡ ⎤ + ⎢ + + ⎣ = ⎥ ⎦

例3求方程dy 1 的通解. dx x+y 解:把所给方程变形 dx=x+y,即 x-x=y. d d d 显然,这是一个一阶线性微分方程: 这里p(y)=-1,q(y)=y. 于是,所求通解为 m dyc) -e(Jye'dy+c) =Ce'-y-1 2009年7月27日星期一 10 目录 上页 下页 返回
2009年7月27日星期一 10 目录 上页 下页 返回 例 3 求方程 d 1 d y x x y = + 的通解. 解 :把所给方程变形为 d d x x y y = + ,即 d d x x y y − = . 显然,这是一个一阶线性微分方程. 这里 p y() 1 = − , qy y ( ) = . 于是,所求通解为 ( 1) d d ( 1) e ed y y x y y C − − − ∫ ∫ ⎛ ⎞ = ⋅+ ⎜ ⎟ ⎝ ⎠ ∫ e ed ( ) y y y yC − = + ∫ e 1 y = −− C y