
新课引入 在前面研究过的积分中,重积分和曲线积分都可转化 为定积分来计算,因此,我们可猜想: 曲线积分也可转化为重积分来计算 这个猜想是正确的.本节将要介绍的格林公式给出了 平面闭区域D上的二重积分与其边界曲线L上的曲线积 分之间的联系. 另一方面,我们可以利用格林公式得到“平面上积分 与路径无关的条件”和“二元函数的全微分求积的充要 条件”。 2009年7月27日星期一 目录 上页 下页 返回
2009年7月27日星期一 1 目录 上页 下页 返回 新课引入 在前面研究过的积分中,重积分和曲线积分都可转 化 为定积分来计算,因此,我们可猜想: 曲线积分也可转化为重积分来计算. 这个猜想是正确的. 本节将要介绍的格林公式给出 了 平面闭区域 D 上的二重积分与其边界曲线 L 上的曲线积 分之间的联系 . 另一方面,我们可以利用格林公式得到“平面上积分 与路径无关的条件”和“ 二 元函数的全微分求积的充要 条件”

第九章 第三节格林公式 Green Formula) 一、格林公式 二、平面上曲线积分与积分路径无关的条件 三、二元函数的全微分求积 四、小结与思考练习 2009年7月27日星期一 2 目录 上页 下页 、返回
2009年7月27日星期一 2 目录 上页 下页 返回 第三节 格林公式 第九章 (Green Formula) 一、格林公式 二、平面上曲线积分与积分路径无关的条件 三、二元函数的全微分求积 四、小结与思考练习
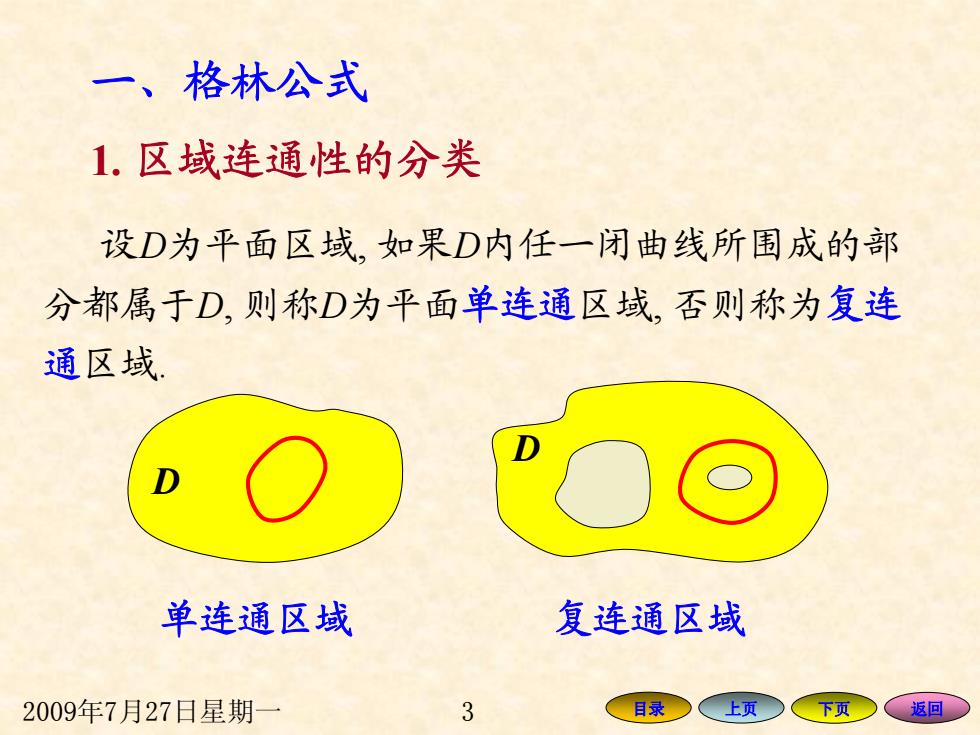
一、格林公式 1.区域连通性的分类 设D为平面区域,如果D内任一闭曲线所围成的部 分都属于D,则称D为平面单连通区域,否则称为复连 通区域」 单连通区域 复连通区域 2009年7月27日星期一 3 目录 上页 下页 返回
2009年7月27日星期一 3 目录 上页 下页 返回 一、格林公式 1. 区域连通性的分类 设D为平面区域, 如果 D内任一闭曲线所围成的部 分都属于 D, 则称 D为平面单连通区域, 否则称为复连 通区域. 单连通区域 复连通区域 D D

2、格林公式 定理1闭区域D由分段光滑的曲线L围成,函 数P(x,y)及Q(x,y)在D上具有一阶连续偏导数, 则有 叮-d-f版+Q (1) 其中L是D的取正向的边界曲线。 公式(1)叫做格林公式 2009年7月27日星期一 4 目录 上页 下页 、返回
2009年7月27日星期一 4 目录 上页 下页 返回 定理 1 闭区域 D由分段光滑的曲线 L围成,函 数 P x y 及 Q x y),(),( 在 D上具有一阶连续偏导数, 则有 ∫∫ ∫ += ∂ ∂ − ∂ ∂ L D dxdy QdyPdx y P x Q )( (1) 其中 L 是 D的取正向的边界曲线。 公式(1)叫做格林公式. 2、格林公式
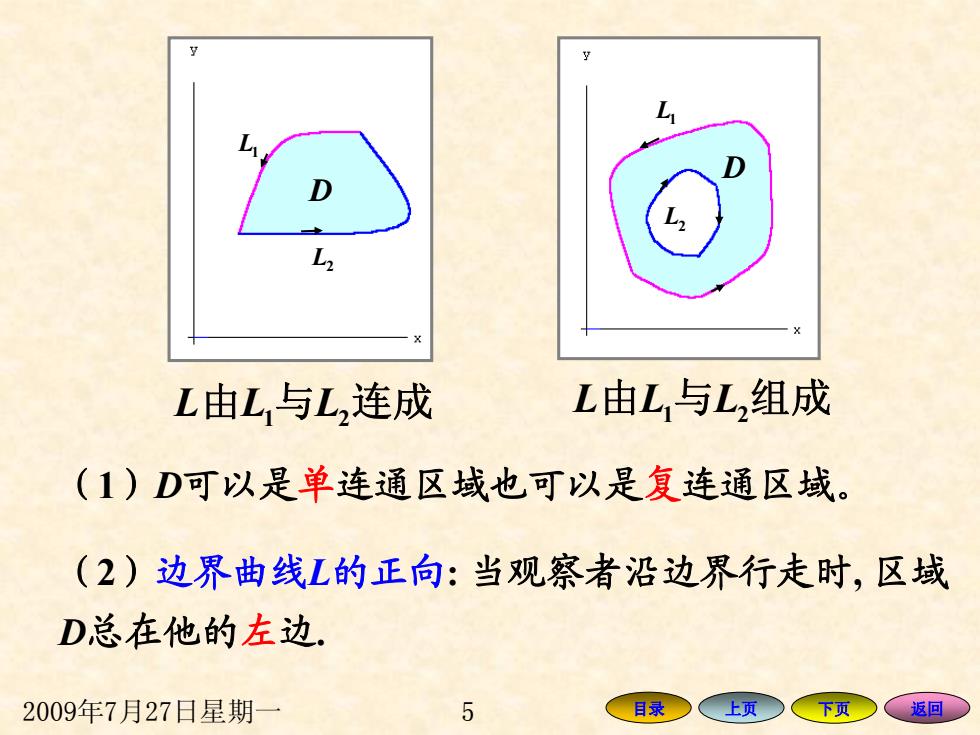
L由L,与L,连成 L由L与L,组成 (1)D可以是单连通区域也可以是复连通区域。 (2)边界曲线L的正向:当观察者沿边界行走时,区域 D总在他的左边. 2009年7月27日星期一 5 目录 上页 下页 返回
2009年7月27日星期一 5 目录 上页 下页 返回 与由 LLL 21 连成 ( 1 ) D可以是 单连通区域也可以是 复连通区域。 L 2 D L1 与由 LLL 21 组成 L 2 L1 D ( 2 )边界曲线 L的正向: 当观察者沿边界行走时, 区域 D总在他的 左 边

证明:(1) Ey=P2(x) 若区域D既是X-型 x=(y) 又是Y-型,即平行于坐 标轴的直线和L至多交 x丰2(y) 于两点. Cy=(x) a b D={(x,y)p(x)≤y≤p2(x),M≤x≤b} D={(x,y)w(y)≤x≤w2(y),c≤y≤} 2009年7月27日星期一 6 目录 上页 下页 返回
2009年7月27日星期一 6 目录 上页 下页 返回 }),()(),{( 1 2 = ϕ ≤ ≤ ϕ ≤ ≤ bxaxyxyxD 证明:(1) 若区域 D既是 X − 型 又是 Y − 型 ,即平行于坐 标轴的直线和 L至多交 于两点. }),()(),{( 1 2 = ψ ≤ ≤ ψ ≤ ≤ dycyxyyxD y x o a b D c d )( 1 y = ϕ x )( 2 y = ϕ x A B C E ( 2 x = ψ y ) )( 1 x = ψ y

I爬a海-424 牛顿莱布 尼兹公式 =了ew,d∫eg,Uw =-上ecw x=vy) -SQ(x.)dy+JcQ(x,y)dy C七=,0) =∮(x,y) 0 同理可证-a-PP 2009年7月27日星期一 7 目录 上页 下页 返回
2009年7月27日星期一 7 目录 上页 下页 返回 dx x Q dydxdy x Q y y d c D ∫∫∫∫ ∂ ∂ = ∂ ∂ )( )( 2 1 ψ ψ ∫ ∫ = − d c d c ψ 2 ψ 1 )),(()),(( dyyyQdyyyQ ∫ ∫ = − CBE CA E ),(),( dyyxQdyyxQ ∫ ∫ = + CBE EA C ),(),( dyyxQdyyxQ ∫ = L ),( dyyxQ 同理可证 ∫∫∫ = ∂ ∂ − L D dxyxPdxdy y P ),( y x o d )(2 x = ψ y D c C E )(1 = ψ yx 牛顿 -莱布 尼兹公式
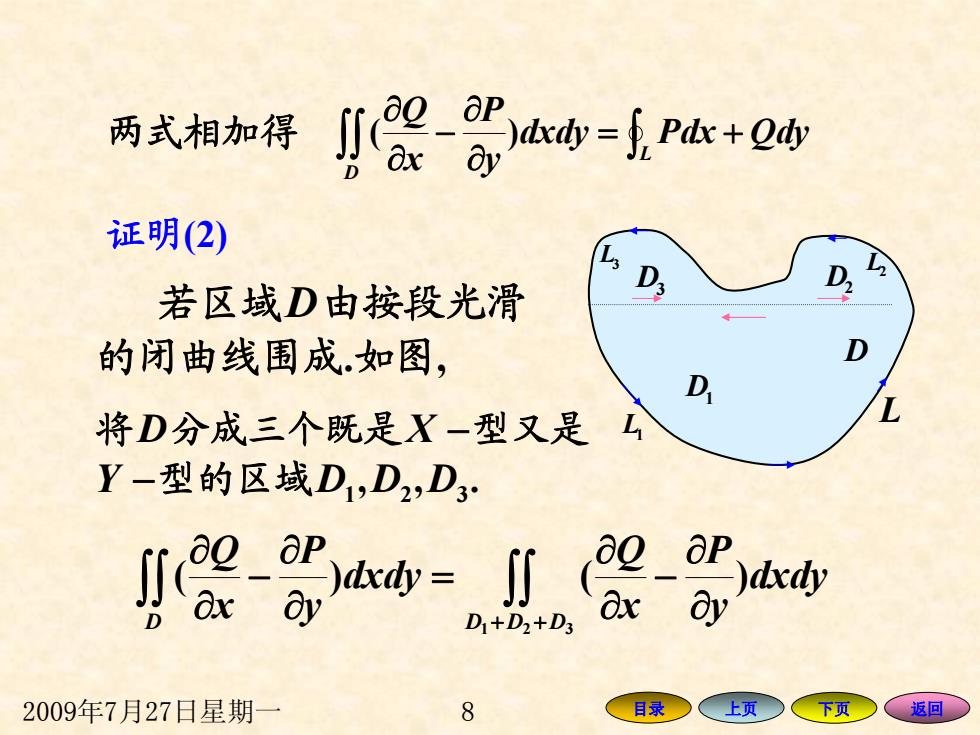
两式相加得 小器-器a-P版+Q购 证明(2) 若区域D由按段光滑 的闭曲线围成如图, D D 将D分成三个既是X-型又是 Y-型的区域D1,D2,D3 小喂-从品h D1+D2+D3 2009年7月27日星期一 8 目录 上页 下页 、返回
2009年7月27日星期一 8 目录 上页 下页 返回 若区域 D由按段光滑 的闭曲线围成 .如图 , 证明(2) L L1 L2 L3 D D1 D3 D2 两式相加得 ∫∫ ∫ += ∂ ∂ − ∂ ∂ L D dxdy QdyPdx y P x Q )( 将 D分成三个既是 X −型又是 Y −型的区域 D 1 , D 2 , D 3 . ∫∫ ∫∫ ++ ∂ ∂ − ∂ ∂ = ∂ ∂ − ∂ ∂ 321 )( )( D DDD dxdy y P x Q dxdy y P x Q

是部+架本+器 =f.Pax+Qdy+fPd+Qdy+f Pax+Qd =人Pk+ L,D (L、L2、L3对D来说为正方向) D 2009年7月27日星期一 0 目录○ 上页 下页 、返回
2009年7月27日星期一 9 目录 上页 下页 返回 ∫∫ ∫∫ ∫∫ ∂ ∂ − ∂ ∂ + ∂ ∂ − ∂ ∂ + ∂ ∂ − ∂ ∂ 1 2 3 )()()( D D D dxdy y P x Q dxdy y P x Q dxdy y P x Q ∫ ∫ ∫ +++++= L1 L 2 L 3 QdyPdx QdyPdx QdyPdx ∫ += L QdyPdx D1 D2 D3 L L1 L2 L3 ( L1 、 L 2 、 L 3 对 D 来说为正方向)

证明(3) 若区域不止由一条闭曲线 所围成.添加直线段AB、CE, 则D的边界曲线由AB,L2,BA, C AFC,CE,L3,EC及GA构成. 2知, =打威打+co去志(Pc+) =(④,+∮+∮P+Qd =P+Q(L、L、L对D来说为正方向.) 2009年7月27日星期一 10 目录 上页 下页 、返回
2009年7月27日星期一 10 目录 上页 下页 返回 G D L 3 L 2 F C E L1 A B 证明(3) 若区域不止由一条闭曲线 所围成.添加直线段 AB 、CE, 则 D的边界曲线由 AB , L 2 ,BA, AFC,CE, L 3, EC 及 GA 构成. 由(2) 知 ∫∫ ∂ ∂ − ∂ ∂ D dxdy y P x Q )( ∫∫ ∫ ∫ ∫ ++++= 2 CEAFCBALAB { ∫ ∫ ∫ +⋅+++ CGAECL (} QdyPdx ) 3 231 ( )( ) LLL = ++ + Pdx Qdy vvv ∫∫∫ ∫ += L QdyPdx ( L1 、 L 2 、 L3 对 D 来说为正方向。 )