
第七章 第六节多元微分学在儿何上的寇用 (Applications of differential calculus in geometry) 一、空间曲线的切线与法平面 二、曲面的切平面与法线 三、小结与思考练习 2009年7月6日星期一 1 目录 上页 下页 、返回
2009年7月6日星期一 1 目录 上页 下页 返回 第六节 多元微分学在几何上的应用 第七章 (Applications of differential calculus in geometry) 一、空间曲线的切线与法平面 二、曲面的切平面与法线 三、小结与思考练习

复习:平面曲线的切线与法线 已知平面光滑曲线y=f(x)在点(xo,0)有 切线方程y-y0=f'(x)(x-xo) 1 法线方程y-0= f(xo (x-x0) 若平面光滑曲线方程为F(x,y)=0,因 dy F(x,y) dx F(x,y) 故在点(x0,0)有 切线方程F(xo,yo)(x-xo)+F,(xo,y0Xy-yo)=0 法线方程Fy(x0,y0)x-xo)-Fx(xo,y0)(y-0)=0 2009年7月6日星期一 2 目录○ 上页 下页 返回
2009年7月6日星期一 2 目录 上页 下页 返回 复习 : 平面曲线的切线与法线 已知平面光滑曲线 y = f x)( ),( 00 x y 切线方程 0 y − y 法线方程 0 y − y 若平面光滑曲线方程为 xF y = ,0),( ),( ),( d d yxF F x y x y y x −= 故在点 ),( 00 x y 切线方程 法线方程 )( 0 )(),( + Fy yx 00 ),( y − y 00 0 F x y xx x − = 0 ))(( 00 = f ′ − xxx )()( 1 0 0 xx xf − ′ −= 有 因 在点 有 0)(),( y yxF 00 ),( − xx 0 )( − x xF y00 y − y 0 =
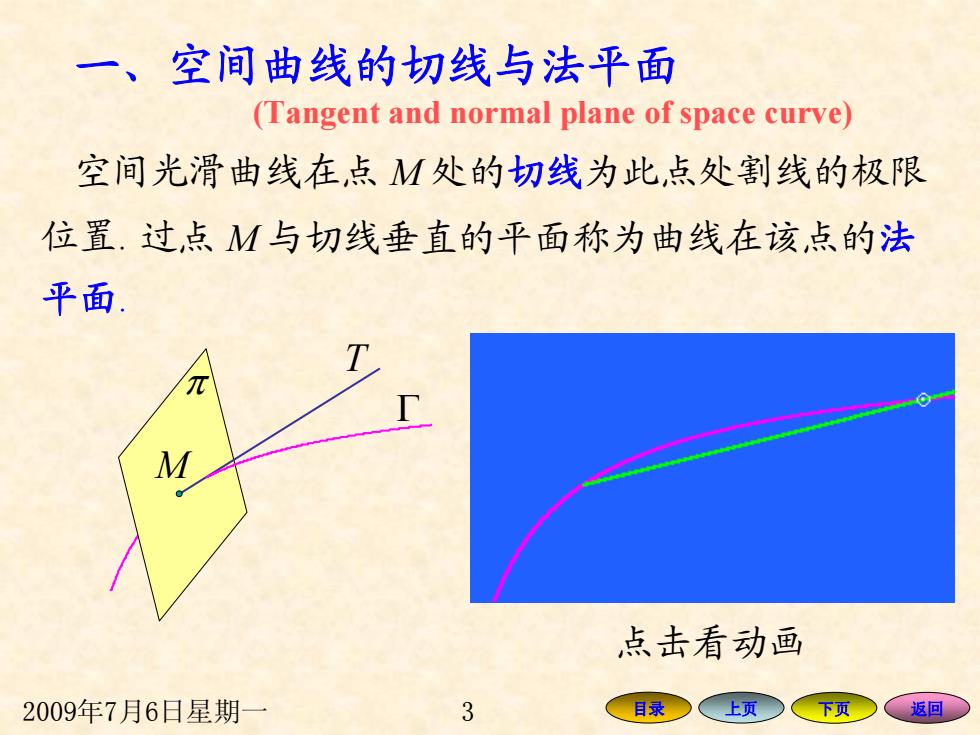
一、空间曲线的切线与法平面 (Tangent and normal plane of space curve) 空间光滑曲线在点M处的切线为此,点处割线的极限 位置.过,点M与切线垂直的平面称为曲线在该,点的法 平面. T 点击看动画 2009年7月6日星期一 3 目录○ 上页 下页 、返回
2009年7月6日星期一 3 目录 上页 下页 返回 一、空间曲线的切线与法平面 位置. 过点 M 与切线垂直的平面称为曲线在该点的 法 空间光滑曲线在点 M 处的切线为此点处割线的极限 平面. 点击看动画 Γ T M π (Tangent and normal plane of space curve)

1.曲线方程为参数方程的情况 T:x=p(t),y=w(t),z=@(t) M 设t=t对应M(x0,y0,20) t=0+△t对应M'(x+△x,yo+Ay,0+△z) 割线M'的方程: X-0-y-y0-2-20 △x Ay △z 上述方程之分母同除以△1,令△t→0,得 切线方程 x-0=y-y0=2-20 e'(to)w(to) 0'(40) 2009年7月6日星期一 4 目录○ 上页 下页 、返回
2009年7月6日星期一 4 目录 上页 下页 返回 Γ x = ϕ t y = ψ t z = ω t)(,)(,)(: z z z y yy x x x Δ − = Δ − = Δ − 0 0 0 上述方程之分母同除以 Δ t , 令 Δ t → ,0 得 切线方程 0 0 0 yyxx z − z = − = − ),( 0 000 设 = 对应 zyxMtt ),( 0 0 0 0 = Δ+ 对应 ′ + Δ + Δ + ΔzzyyxxMttt )( 0 ϕ ′ t )( 0 ψ′ t )( 0 ω′ t T M Γ M ′ 割线 MM ′的方程: 1. 曲线方程为参数方程的情况

此处要求0(to),w'(to),0'(to)不全为0, 如个别为0,则理解为分子为0 切线的方向向量: T=(@(to),w(to),@'(to) 称为曲线的切向量. 下也是法平面的法向量,因此得法平面方程 0'(tx-x)+y'(t0)(y-y0+0'(t0(z-20)=0 说明若引进向量函数r(t)=(0(t),y(t),o(t),则「 为r()的矢端曲线,而在0处的导向量 F(to)=(o'(to),y'(4o),0'(to) 就是该点的切向量 2009年7月6日星期一 5 目录 (上页 下页 、返回
2009年7月6日星期一 5 目录 上页 下页 返回 ))(( 00 ϕ′ t x − x 此处要求 )(,)(,)( 000 ϕ′ t ψ′ t ω′ t 也是法平面的法向量, )()( 0 0 yy 切线的方向向量: 称为曲线的切向量 . + ψ′ t − 0))(( + ω′ t z − z00 = 如个别为0, 则理解为分子为 0 . π M Γ 不全为0, ))(,)(,)(( 000 T = ϕ′ t ψ′ t ω′ t T 因此得法平面方程 说明 : 若引进向量函数 r t = ϕ t ψ t ω t ))(,)(,)(()( , 则 Γ 为 r ( t) 的矢端曲线, 0 而 在 t ))(,)(,)(()( 0 000 处的导向量 r′ t = ϕ′ t ψ′ t ω′ t 就是该点的切向量. o r t)( T

例1求曲线x=cost,y=sint,z=2t在对应于 6-的点处的切线方程和法平面方程 解题思路:T:x=p(t),y=w(t),z=o(t) 设t=t0对应M(x0,y0,20) 切线方程 x-0=y-y0=2-20 p'(to)'(to)o'()》 法平面方程 p'(tox-x0)+w'(t0)(y-y0)+o'(0)(z-20)=0 2009年7月6日星期一 6 目录 上页 下页 返回
2009年7月6日星期一 6 目录 上页 下页 返回 例 1 求曲线 x = cos t , y t = sin , z = 2 t 在对应于 0 4 t π = 的点处的切线方程和法平面方程. 解题思路 : Γ x = ϕ t y = ψ t z = ω t)(,)(,)(: ),( 0 000 设 = 对应 zyxMtt 切线方程 0 0 0 x x yy z − z = − = − )( 0 ϕ ′ t )( 0 ψ′ t )( 0 ω′ t 法平面方程 ))(( 00 ϕ′ t x − x )()( 0 0 + ψ′ t − yy 0))(( + ω′ t z − z00 =

如果曲线厂由方程组y=y(x),z=(x)给出, 只要将此方程组改写为以x为参数的参数方程 x=x, y=(x), =(x), 则根据上面的讨论可知,T上点M(x,y,20)处的切 向量为 T=(1,y'(x),z'(x) 2009年7月6日星期一 7 目录○ (上页今 下页 、返回
2009年7月6日星期一 7 目录 上页 下页 返回 如果曲线 Γ 由方程组 y yx = ( ), z = z x( )给出, 只要将此方程组改写为以 x为参数的参数方程 , ( ), ( ), x x y yx z z x ⎧ = ⎪ ⎨ = ⎪ ⎩ = 则根据上面的讨论可知, Γ 上点 00 00 M (, ,) xyz 处的切 向量为 0 0 T = (1, ( ), ( )) yx zx ′ ′

2.曲线为一般式的情况 光计齿改1{瓷)=8 当J= (F,G)+0时,「可表示为 ∫y=p(x) a(y,z) 2=w(x 且有 dy 1(F,G)dz 1a(F,G) dxJa(z,x)’dxJa(x,y) 曲线上一点M(x0,y0,20)处的切向量为 y+2 T={1,p'(x0),'(xo)} 十6 1a(F,G) M'⊙(x,y) M 2009年7月6日星期一 8 目录 上页 下页 返回
2009年7月6日星期一 8 目录 上页 下页 返回 光滑曲线 ⎩ ⎨ ⎧ = = Γ 0),( 0),( : zyxG zyxF 当 0 ),( ),( ≠ ∂ ∂ = zy F G J ⎩ ⎨ ⎧ = = )( )( xz xy ψ ϕ = x y d d 曲线上一点 ),( 000 zyxM x y z , 且有 = x z d d , ),( ),(1 xz F G J ∂ ∂ , ),( ),(1 yx F G J ∂ ∂ 处的切向量为 时, Γ 可表示为 ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ∂ ∂ ∂ ∂ = M yx M GF Jxz GF J ),( ),(1 , ),( ),(1,1 { })(,)(,1 0 0 T = ϕ′ ψ′ xx 2. 曲线为一般式的情况

或7= a(F,G) o(,G) @(F,G) a(y,=) M’d (2,x)M’a(x,y) M 则在点M(x0,y0,20)有 x-x0 y-yo 2-20 切线方程 &F,G) a(F,G) &(F,G) a(y,2) M a(z,x) M a(x,y) M 法平面方程 a(F,G) (x-x0)+ @(F,G) (y,2) a(z,x) (y-yo) &(F,G) (z-20)=0 d(x,y) M 2009年7月6日星期一 9 目录今 上页 下页 返回
2009年7月6日星期一 9 目录 上页 下页 返回 0 0 0 xx yy z − z = − = − zy M GF ),( ),( ∂ ∂ 则在点 ),( 000 M x y z 切线方程 法平面方程 有 zy M GF ),( ),( ∂ ∂ xz M GF ),( ),( ∂ ∂ yx M GF ),( ),( ∂ ∂ )( 0 − xx yx M GF ),( ),( ∂ ∂ + xz M GF ),( ),( ∂ ∂ + )( 0 y − y 0)(z − z 0 = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ∂ ∂ ∂ ∂ ∂ ∂ = M M yx M GF xz GF zy GF T ),( ),( , ),( ),( , ),( ),( 或

法平面方程 &(F,G) 8y2)Mx-o)+ (F,G) (z,x) MOy-o》 &F,G) x,)M(2-0)=0 也可表为 x-x0 y-Y0 2-20 Fx(M)F(M)F(M) =0 Gx(M)Gy(M)G(M) 2009年7月6日星期一 10 目录 上页 下页 、返回
2009年7月6日星期一 10 目录 上页 下页 返回 0 )()()( )()()( 0 0 0 = −−− MGMGMG MFMFMF zzyyxx x y z x y z 也可表为 )( ),( ),( )( ),( ),( 0 0 yy xz M GF xx zy M GF − ∂ ∂ +− ∂ ∂ 0)( ),( ),( 0 =− ∂ ∂ + zz yx M GF 法平面方程