
新课引入 前面讨论的定积分,都是在有限区间上的有界函数 的积分,这类积分属于通常意义下的积分 但在实际问题中,还会遇到积分区间为无限或被积 函数在积分区间上是无界的情况, 这就需将定积分的概念推广,推广后的积分被称为 广义积分. 积分限有限 推广无穷限的广义积分 常义积分 被积函数有界◆无界函数的广义积分 2009年7月3日星期五 目录 上页 下页 返回
2009年7月3日星期五 1 目录 上页 下页 返回 新课引入 前面讨论的定积分,都是在有限区间上的有界函数 的积分,这类积分属于通常意义下的积分. 但在实际问题中,还会遇到积分区间为无限或被积 函数在积分区间上是无界的情况, 这就需将定积分的概念推广,推广后的积分被称为 广义积分. 常义积分 积分限有限 被积函数有界 推广 无穷限的广义积分 无界函数的广义积分

第五章 第四节广义积分 Improper Integrals) 一、无穷限的广义积分 二、无界函数的广义积分 三、思考与练习 2009年7月3日星期五 2 目录○ 、上页(下页 返回
2009年7月3日星期五 2 目录 上页 下页 返回 第四节 广义积分 第五章 (Improper Integrals) 二、无界函数的广义积分 一、无穷限的广义积分 三、思考与练习
一、无穷限(Infinite Intervals)的广义积分 引例曲线少平和直线-1及x锁所回成的并口曲 边梯形的面积可记作 y 其含义可理解为 -m8-1 2009年7月3日星期五 3 目录○ (上页今 下页 、返回
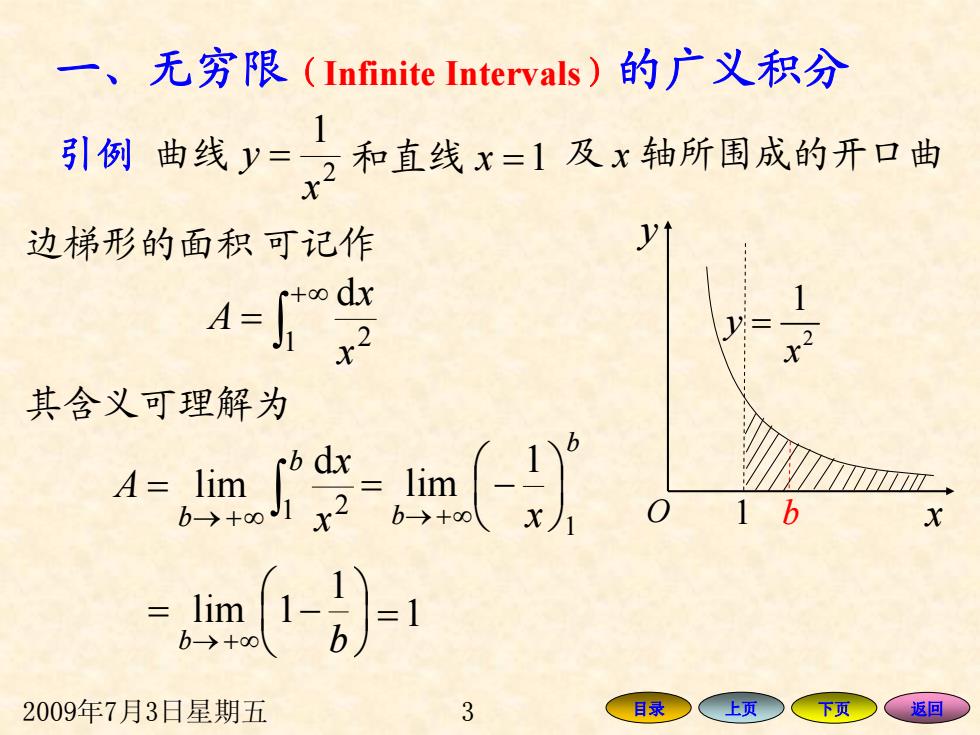
2009年7月3日星期五 3 目录 上页 下页 返回 一、无穷限 (Infinite Intervals )的广义积分 引例 曲线 2 1 x y = 和直线 x = 1 及 x 轴所围成的开口曲 边梯形的面积 可记作 ∫ ∞+ = 1 2 d x x A 其含义可理解为 ∫ ∞+→ = b b x x A 1 2 d lim b b x 1 1 lim ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −= ∞+→ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −= b ∞+→ b 1 1lim = 1 O x y 1 2 1 y x = b

定义1设f(x)∈C[a,+o),取b>a,若 nds 存在,则称此极限为f(x)的无穷限广义积分,记作 d-d 这时称广义积分∫f(x)dx收敛;如果上述极限不存在, 就称广义积分f(x)dr发散. 类似地,若f(x)∈C(-o,b],则定义 (x)dx=limf)dx 2009年7月3日星期五 4 目录 上页 下页 返回
2009年7月3日星期五 4 目录 上页 下页 返回 f ∈ aCx + ∞ ,),[)( 取 > ab , 若 xxf b b a∫ d)(lim∞+→ 存在 , 则称此极限为 f (x) 的无穷限广义积分, 记作 xxf xxf b a b a d)(limd)( ∫ ∫ ∞+→ + ∞ = 这时称广义积分 xxf a d)( ∫ + ∞ 收敛 ; 如果上述极限不存在, xxf a d)( 就称广义积分 ∫ + ∞ 发散 . 类似地 , 若 f x ∈ C − ∞ b ,],()( 则定义 xxf xxf b a a b d)(limd)( ∫ ∫ ∞− ∞−→ = 定义1 设

若f(x)∈C(-0,+o),则定义 「fd-lmfx)dx+mf)d (c为任意取定的常数) 只要有一个极限不存在,就称∫f(x)dx发散. 无穷限的广义积分也称为第一类广义积分 说明:上述定义中若出现0-0,并非不定型, 它表明该广义积分发散· 2009年7月3日星期五 5 目录 上页> 下页 、返回
2009年7月3日星期五 5 目录 上页 下页 返回 若 Cxf −∞∈ + ∞ ,),()( 则定义 = ∫ + ∞ ∞− d)( xxf xxf c a a∫ d)(lim∞−→ xxf b b c∫ d)(lim∞+→ + ( c 为任意取定的常数 ) 只要有一个极限不存在 , 就称 d)( xxf ∫ ∞+∞− 发散 . 无穷限的广义积分也称为第一类广义积分. 说明 : 上述定义中若出现 ∞ − ∞ ,并非不定型 , 它表明该广义积分发散

若F(x)是f(x)的原函数,引入记号 F(+oo)=lim F(x);F(-o)=lim F(x) X→+0 X→-00 则有类似牛一莱公式的计算表达式: fd=F”-Fw-ra) F-F() 广f=atF4)-F 2009年7月3日星期五 6 目录 上页 下页 、返回
2009年7月3日星期五 6 目录 上页 下页 返回 是若 xfxF 的原函数 ,)()( 引入记号 F xF ;)(lim)( x ∞+→ =+∞ F xF )(lim)( x ∞−→ − ∞ = 则有类似牛 – 莱公式的计算表达式 : xxf a d)( ∫ + ∞ = F x)( a + ∞ = F + ∞ − F a)()( xxf b d)( ∫ ∞− = F x)( − ∞ b = F b − F − ∞)()( d)( xxf ∫ + ∞ ∞− = F x)( − ∞ + ∞ = F +∞ − F − ∞)()(

例19明花无p报分票当p1时牧敛,p 时发散.(课本例2) 证:当p=1时有 -ag- 当p≠1时有 - p1 al-p 因此,当p>1时,广义积分收敛,其值为 D-1 当p≤1时,广义积分发散 2009年7月3日星期五 目录 上页 下页 返回
2009年7月3日星期五 7 目录 上页 下页 返回 ∫ ∞+ a p x dx 证 : 当 p =1 时有 ∫ ∞+ a x dx [ ] + ∞ = a ln x = + ∞ ∫ ∞+ a p x dx − + ∞ ⎥⎦ ⎤ ⎢⎣ − ⎡ = a p p x 1 1 ⎩ ⎨ ⎧ = 当 p ≠ 1 时有 p 1 1 1 − − p a p , 当 p >1 时收敛 ; p ≤1 时发散 . + ∞ 因此, 当 p > 1 时, 广义积分收敛 , 其值为 ; 1 1 − − p a p 当 p ≤ 1 时, 广义积分发散 . 例1 证明第一类 p 积分 (课本 例 2 )

如计广汉软分 解=ann子( 思专0对吗? 分标-0+ 十 原积分发散! 注意:对广义积分,只有在收敛的条件下才能使用 “偶倍奇零”的性质,否则会出现错误 2009年7月3日星期五 8 目录 上页 下页 返回
2009年7月3日星期五 8 目录 上页 下页 返回 . 1 d ∫ 2 ∞+ ∞− + x x 解 : ∫ ∞+∞− + 2 1 d x x + ∞ − ∞ = x ]arctan[ ) 2 ( π −− 2 π = = π 思考: ?0 1 d 2 = 对吗 + ∫ ∞+∞− x xx 分析 : ∞− ∞+ ∞+ ∞− += + ∫ )1ln( 2 1 1 d 2 2 x x xx 原积分发散 ! 注意 : 对广义积分, 只有在收敛的条件下才能使用 “偶倍奇零 ” 的性质, 否则会出现错误 . 例2 计算广义积分

二、无界函数(Unbounded Functions)的广义积分 引例曲线与x轴y轴和直线x=1所国成的 开口曲边梯形的面积可记作 y 1- 其含义可理解为 x A=limd女-1im2v 1 60tVx60 =lim2(1-√8)=2 8→01 2009年7月3日星期五 9 目录 上页 下页 返回
2009年7月3日星期五 9 目录 上页 下页 返回 二、无界函数 (Unbounded Functions )的广义积分 引例 :曲线 x y 1 = 与 x 轴, y 轴和直线 x = 1 所围成的 开口曲边梯形的面积 O x y 1 y x = ε 1 可记作 ∫ = 1 0 d x x A 其含义可理解为 + ∫ → = 1 0 d lim ε ε x x A ε ε 1 2lim0 x → + = )1(2lim0 ε ε = − → + = 2

定义2设f(x)∈C(a,b],而在点a的右邻域内无界 取e>0,若极限1im白.f(x)dr存在,则称此极限为函 -→0+Ja+8 数f(x)在[a,b]上的广义积分,记作 0Jfo)dr=lim克f0dr →0+a+s 这时称广义积分fx)dr收敛;如果上述极限不存在, 就称广义积分f(x)dr发散. 类似地,若f(x)∈C[a,b),而在b的左邻域内无界, 则定义 ods 2009年7月3日星期五 10 目录 上页 下页 返回
2009年7月3日星期五 10 目录 上页 下页 返回 f ∈ baCx ,],()( 而在点 a 的右邻域内无界, 取 ε > ,0 存在 , xxf xxf b a b a d)(limd)( 0 ∫ ∫ → + + = ε ε xxf b a d)( ∫ 就称广义积分 xxf b a d)( ∫ 类似地 , 若 baCx ,),[)( 这时称广义积分 收敛 ; 如果上述极限不存在, 发散 . f ∈ 而在 b 的左邻域内无界, xxf xxf b a b a d)(limd)( 0 ∫ ∫ − → + = ε ε 若极限 ∫ → + + b a xxf ε ε d)(lim0 则称此极限为函 定义2 设 数 f (x) 在 [ a , b] 上的广义积分, 记作 则定义