
第五章 第五节定积分的元素法及其应用 Element Method of Definite Integral and Its Applications) 一、定积分的元素法 二、定积分在几何学上的应用 三、定积分在物理学上的应用 四、思考与练习 2009年7月3日星期五 1 目录○ 上页 下页 返回
2009年7月3日星期五 1 目录 上页 下页 返回 第五节 定积分的元素法及其应用 第五章 (Element Method of Definite Integral and Its Applications ) 二、定积分在几何学上的应用 一、定积分的元素法 三、定积分在物理学上的应用 四、思考与练习

三、定积分在物理学上的应用 1.变力沿直线所作的功 设物体在连续变力F(x)作用下沿x轴从x=a移动到 x=b,力的方向与运动方向平行,求变力所做的功. 在[a,b]上任取子区间[x,x+dx],在其上所作的功元 素为 dW=F(x)dx a x x+dx h x 因此变力F(x)在区间[a,b]上所作的功为 w=F(x)dx 2009年7月3日星期五 2 目录 上页今 下页 、返回
2009年7月3日星期五 2 目录 上页 下页 返回 三、定积分在物理学上的应用 1. 变力沿直线所作的功 设物体在连续变力 F(x) 作用下沿 x 轴从 x =a 移动到 x = b , 力的方向与运动方向平行, 求变力所做的功 . a x x + d x b x 在 [ a,b ]上任取子区间 [ x, x + d x ],在其上所作的功元 素为 d W = F ( x ) dx 因此变力 F(x) 在区间 [ a,b ]上所作的功为 ∫ = b a W F ( x ) dx

例1已知一弹簧拉长0.02m要用9.8N的力,求把该弹 簧拉长0.1m所作功.(课本例11) 解:由物理学中的胡克定理可知,在 弹性限度内拉伸弹簧所需要的力与弹 簧的伸长量x成正比,即 分 白- F=k·x(k为比例系数) x+dx 根据题意,当x=0.02m时,F=9.8N, F=kx 所以k=4.9×102,即F=4.9×102x 设弹簧沿着x轴正方向拉伸,则x的变化范围为[0,0.1] 在[0,0.1]上任取一小区间[x,x+dx](如图),与该小区间 对应的变力F可近似地看作常力,因此在此小区间上力F所 2009年7月3日星期五 3 目录 上页 下页 返回
2009年7月3日星期五 3 目录 上页 下页 返回 例 1 已知一弹簧拉长0.02 m 要用9.8 N 的力,求把该弹 簧拉长0.1 m 所作功. (课本 例 11 ) F = k x⋅ 解:由物理学中的胡克定理可知, 在 弹性限度内拉伸弹簧所需要的力与弹 簧的伸长量 x 成正比,即 ( k为比例系数) 根据题意,当 x = 0.02 m 时, F = 9.8 N, 所以 2 k = × 4.9 10 ,即 2 F = 4.9 10 × x 设弹簧沿着 x 轴正方向拉伸,则 x 的变化范围为[0, 0.1], 在[0, 0.1] 上任取一小区间[, d ] xx x + (如图),与该小区间 对应的变力 F 可近似地看作常力,因此在此小区间上力 F 所

功W的元素为 dW=4.9×102xdx 于是弹簧拉长0.1m所作的功为 W=∫49x102xdx =4910 =2.45(J) 2009年7月3日星期五 4 目录 上页( 下页 返回
2009年7月3日星期五 4 目录 上页 下页 返回 功 W 的元素为 2 d d W x = 4.9 0 × 1 x 于是弹簧拉长0.1m 所作的功为 2 0.1 0 W = 4.9 10 d × x x ∫ 0.1 2 2 0 4.9 10 2 ⎡ x ⎤ = × ⎢ ⎥ ⎣ ⎦ = 2.45 ( ) J
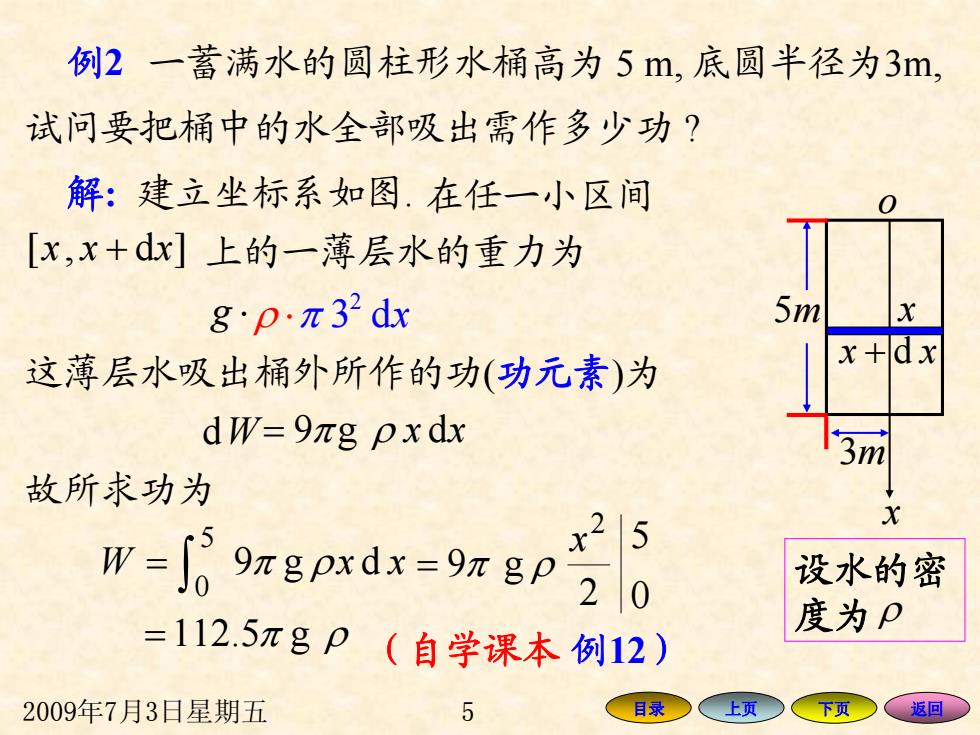
例2一蓄满水的圆柱形水桶高为5m,底圆半径为3m, 试问要把桶中的水全部吸出需作多少功? 解:建立坐标系如图.在任一小区间 [x,x+dx]上的一薄层水的重力为 8pπ32dx 5m 这薄层水吸出桶外所作的功(功元素)为 x+dx dW=9πg pxdx 3m 故所求功为 2 W=的9πBpxdx=9zg 5 设水的密 ,0 =112.5πgP(自学课本例12) 度为P 2009年7月3日星期五 5 目录 上页 下页 返回
2009年7月3日星期五 5 目录 上页 下页 返回 试问要把桶中的水全部吸出需作多少功 ? 解 : 建立坐标系如图. o x 3 m x + d xx 5 m 在任一小区间 + xxx ]d,[ 上的一薄层水的重力为 g ⋅ 2 ρ ⋅π 3 dx 这薄层水吸出桶外所作的功 (功元素 ) 为 d W = 9 π g ρ x dx 故所求功为 ∫ = 5 0 W 9 π g ρx d x = π g9 ρ 2 2 x = π g5.112 ρ 设水的密 度为 ρ 0 5 (自学课本 例12 ) 例 2 一蓄满水的圆柱形水桶高为 5 m, 底圆半径为3m
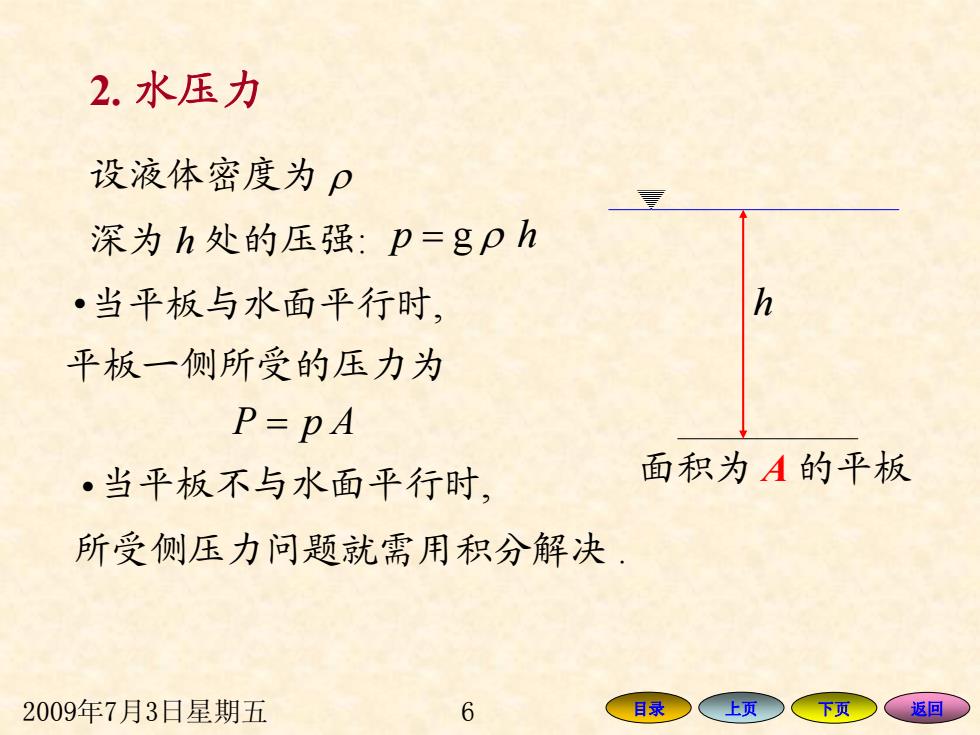
2.水压力 设液体密度为p 深为h处的压强:p=gph ·当平板与水面平行时, h 平板一侧所受的压力为 P=PA ·当平板不与水面平行时, 面积为A的平板 所受侧压力问题就需用积分解决 2009年7月3日星期五 6 目录 上页今 下页 、返回
2009年7月3日星期五 6 目录 上页 下页 返回 面积为 A 的平板 设液体密度为 ρ 深为 h 处的压强: = g ρ hp 当平板与水面平行时, h = ApP 当平板不与水面平行时, 所受侧压力问题就需用积分解决 . 平板一侧所受的压力为 • • 2. 水压力
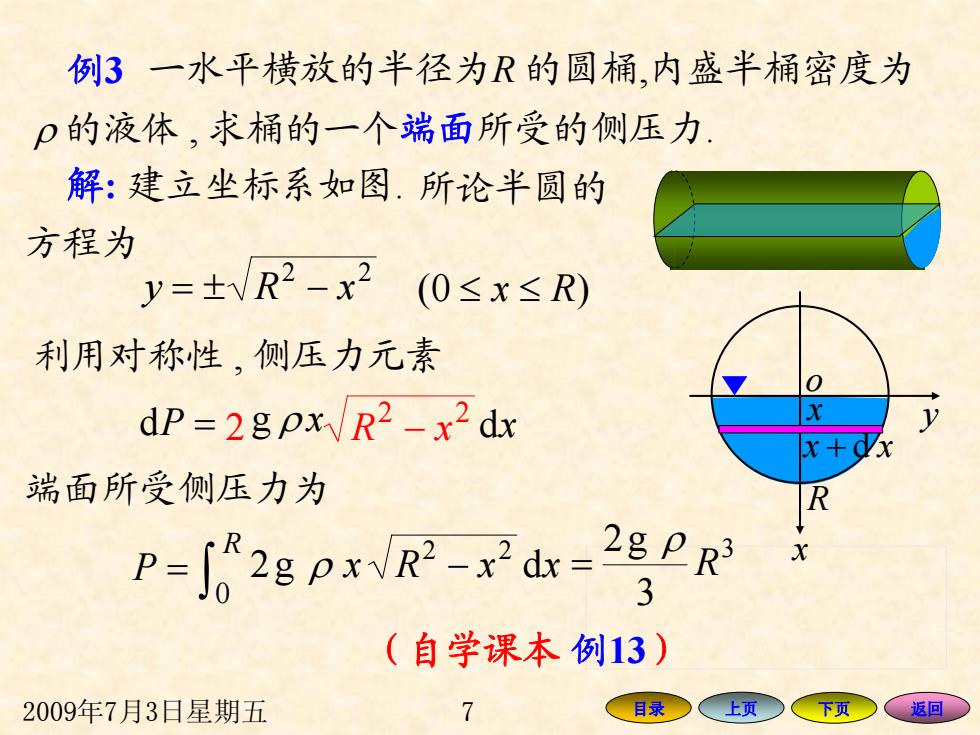
例3一水平横放的半径为R的圆桶,内盛半桶密度为 p的液体,求桶的一个端面所受的侧压力 解:建立坐标系如图.所论半圆的 方程为 y=±WR2-x2(0≤x≤R) 利用对称性,侧压力元素 dP=2gpxR2-x2 dx c+0 端面所受侧压力为 P-f28PxVR-x dx-280R 3 (自学课本例13) 2009年7月3日星期五 7 目录 上页 下页 返回
2009年7月3日星期五 7 目录 上页 下页 返回 小窄条上各点的压强 ≈ g ρ xp 3 3 g2 R ρ = ρ 的液体 , 求桶的一个端面所受的侧压力. 解 : 建立坐标系如图. 所论半圆的 22 −±= xRy ≤ x ≤ R)0( 利用对称性 , 侧压力元素 ∫ = R P 0 g2 dxxRx 22 ρ − o x y R x x + d x 22 d P = 2 g ρ x − xR dx 方程为 端面所受侧压力为 例 3 一水平横放的半径为 R 的圆桶,内盛半桶密度为 (自学课本 例13 )

说明:当桶内充满液体时,小窄条上的压强为gP(R+x) 侧压力元素dP=2gp(R+x人WR2-x2dx, 故端面所受侧压力为 P=∫2gp(R+xWR2-x2dx y -4RgP[R2-xdx 奇函数 x+dx R 令x=Rsint snel5a-n6 =πgpR3 2009年7月3日星期五 8 目录 、上页 下页 返回
2009年7月3日星期五 8 目录 上页 下页 返回 [ ] 0 arcsin 2 2 g4 2 22 R R xR xR x = R ρ +− 2 ,d22 − xxR 当桶内充满液体时,小窄条上的压强为 g ρ R + x ,)( 侧压力元素 d P = 故端面所受侧压力为 ∫− = −+ R R P d)(g2 xxRxR 22 ρ 奇函数 3 = g ρπ R g ρ R + x)( ∫ = − R xxRR 0 22 g4 ρ d 令 = sin tRx o x y R x x + d x 说明 :

3.引力 质量分别为m1,m2的质点,相距r, 1m2 二者间的引力: 大小:F=km2 方向:沿两质点的连线 若考虑物体对质点的引力,则需用积分解决」 2009年7月3日星期五 9 目录 上页 下页 、返回
2009年7月3日星期五 9 目录 上页 下页 返回 质量分别为 21 , mm 的质点 , 相距 r , m 1 r m 2 二者间的引力 : 大小: 2 21 r mm = kF 方向: 沿两质点的连线 若考虑物体对质点的引力, 则需用积分解决 . 3. 引力

例4设有一长度为1,线密度为山的均匀细直棒,在 其中垂线上距a单位处有一质量为m的质,点M,试计算 该棒对质点的引力.(课本例14) 解:建立坐标系如图.细棒上小段 a [x,x+d]对质,点的引力大小为 dF, dF=k mudx dF a2+x2 故垂直分力元素为 xx+dx 0 I x dFy=-dFcosa - 2 =-k mu do a dx a2+x2a2+x2 2 =-kmua (a2+x2)月 2009年7月3日星期五 10 目录 (上页 下页 返回
2009年7月3日星期五 10 目录 上页 下页 返回 设有一长度为 l, 线密度为 μ 的均匀细直棒, 其中垂线上距 a 单位处有一质量为 m 的质点 M, M 该棒对质点的引力. (课本 例14 ) 解 : 建立坐标系如图. y 2 l 2 l − + dxxx ],[ 细棒上小段 对质点的引力大小为 d = kF μ dxm 22 + xa 故垂直分力元素为 y −= FF cosdd α a ⋅ + −= 22 d xa xm k μ 22 xa a + 2 3 )( d 22 xa x amk + −= μ a o x x α 在 试计算 d F d Fx d Fy + d xx 例 4