
第六章 第三节曲面及其方程 (Surface and Its Equation) 一、曲面方程的概念 二、旋转曲面 三、柱面 四、二次曲面 五、小结与思考练习 2009年7月3日星期五 1 目录 上页 下页 、返回
2009年7月3日星期五 1 目录 上页 下页 返回 第三节 曲面及其方程 第六章 (Surface and Its Equation ) 四、二次曲面 一、曲面方程的概念 二、旋转曲面 三、柱 面 五、小结与思考练习

一、曲面方程的概念(Equations for a Surface) 引例:求到两定点A(1,2,3)和B(2,-1,4)等距离的点的 轨迹方程. 解:设轨迹上的动点为M(x,y,z),则AM=BM,即 V(x-1)2+(y-2)2+(z-3)2 =V(x-2)2+(y+1)2+(z-4)2 化简得2x-6y+2z-7=0 说明:动,点轨迹为线段AB的垂直平分面. 1:显然在此平面上的点的坐标都满足此方程, 2:不在此平面上的点的坐标不满足此方程 2009年7月3日星期五 2 目录 上页 下页 返回
2009年7月3日星期五 2 目录 上页 下页 返回 一、曲面方程的概念 求到两定点 A(1,2,3) 和 B(2,-1,4)等距离的点的 2 2 2 zyx −+−+− )3()2()1( 化简得 x − y + z − = 07262 即 说明: 动点轨迹为线段 AB 的垂直平分面. 引例: 1:显然在此平面上的点的坐标都满足此方程, 2:不在此平面上的点的坐标不满足此方程. 2 2 2 zyx −+++−= )4()1()2( 解:设轨迹上的动点为 M x y z ,),( 则 = BMAM , 轨迹方程. (Equations for a Surface)

定义1如果曲面S与方程F(x,y,z)=0有下述关系: (1)曲面S上的任意点的坐标都满足此方程; (2)不在曲面S上的,点的坐标不满足此方程, 则F(x,yz)=0叫做曲面S的方程, F(x,y,2)=0 曲面S叫做方程F(x,y,z)=0的图形 Z 两个基本问题: (1)已知一曲面作为点的几何轨迹时, 求曲面方程。 (2)已知方程时,研究它所表示的几何形状 (必要时需作图). 2009年7月3日星期五 3 目录 上页 下页 、返回
2009年7月3日星期五 3 目录 上页 下页 返回 F x y z = 0),( S z y x o 定义 1 如果曲面 S 与方程 F( x, y, z ) = 0 有下述关系: (1) 曲面 S 上的任意点的坐标都满足此方程; 则 F( x, y, z ) = 0 叫做曲面 S 的方程, 曲面 S 叫做方程 F( x, y, z ) = 0 的图形. 两个基本问题 : (1) 已知一曲面作为点的几何轨迹时, (2) 不在曲面 S 上的点的坐标不满足此方程, 求曲面方程. (2) 已知方程时 , 研究它所表示的几何形状 ( 必要时需作图 )

例1求动点到定点M0(xo,y0,20)距离为R的轨迹 方程. 解:设轨迹上动点为M(x,y,2),依题意MoM=R 即 V(x-x0)2+(y-0)2+(2-20)2=R 故所求方程为 (x-x)2+(y-)2+(2-20)2=R2 特别,当M在原点时,球面方程为 x2+y2+z2=R2 z=士√R2-x2-y2表示上(下)球面 X 2009年7月3日星期五 4 目录○ 、上页 (下页 、返回
2009年7月3日星期五 4 目录 上页 下页 返回 故所求方程为 M x y z),( ),( 0000 M x y z 方程. 特别,当 M0在原点时,球面方程为 解 : 设轨迹上动点为 0 = RMM 即 依题意 距离为 R 的轨迹 x y z o M M 0 222 −−±= yxRz 表示上 ( 下 )球面 . =−+−+− Rzzyyxx 2 0 2 0 2 0 )()()( 2 2 22 0 00 ( )( )( ) x − +− +− = x yy zz R 2 22 2 xyzR + + = 例1 求动点到定点

例2研究方程x2+y2+z2-2x+4y=0表示怎样 的曲面.(课本例3) 解:配方得(x-1)2+(y+2)2+z2=5 此方程表示:球心为M0(1,-2,0), 半径为√5的球面 说明:如下形式的三元二次方程(A≠0) A(x2+y2+22)+Dx+Ey+Fz+G=0 都可通过配方研究它的图形. 2009年7月3日星期五 5 目录○ 上页 下页 、返回
2009年7月3日星期五 5 目录 上页 下页 返回 042 222 yxzyx =+−++ 解: 配方得 5 ,)0,2,1( 此方程表示: M 0 − 说明: 如下形式的三元二次方程 ( A ≠ 0 ) 都可通过配方研究它的图形. 的曲面. (课本 例 3 ) 表示怎样 半径为 的球面. ( ) 0 222 GFzEyDxzyxA =++++++ 球心为 5)2()1( 2 22 zyx =+++− 例2 研究方程

二、旋转曲面(Surface of Revolution) 定义2一条平面曲线绕其平面上一条定直线旋转 一周所形成的曲面叫做旋转曲面.该定直线称为旋转 轴,旋转曲线叫做旋转曲 面的母线. 例如: 2009年7月3日星期五 6 目录○ 、上页下页 、返回
2009年7月3日星期五 6 目录 上页 下页 返回 定义 2 一条平面曲线 绕其平面上一条定直线旋转 二、旋转曲面 一周所形成的曲面叫做旋转曲面.该定直线称为旋转 轴 ,旋转曲线叫做旋转曲 面的母线. 例如 : (Surface of Revolution)

建立y0z面上曲线C绕z轴旋转所成曲面的方程: 给定y0z面上曲线C:f(y,z)=0 若点M1(0,1,)∈C,则有 f(4,2)=0 当绕z轴旋转时,该点转到 k二SM1(01,) M(x,} M(x,y,),则有 =x+y= 故旋转曲面方程为 f±Vx2+y2,z)=0 2009年7月3日星期五 7 目录 上页 下页 、返回
2009年7月3日星期五 7 目录 上页 下页 返回 故旋转曲面方程为 M x y z ,),( 当绕 z 轴旋转时, 0),( f y z11 = ,),0( 若点 M y z111 ∈ C 给定 yoz 面上曲线 C: ),0( 111 zyM zyxM ),( 1 22 1 = , =+ yyxzz 则有 ( 0), 22 zyxf =+± 则有 该点转到 f y z = 0),( o z y x C 建立yoz面上曲线 C 绕 z 轴旋转所成曲面的方程:

思考:当曲线C绕y轴旋转时,方程如何? 1C:f(y,z)=0 f(y,±Vx2+z2)=0 求旋转曲面方程时,平面曲线绕某坐标轴旋转,则该坐 标轴对应的变量不变,而曲线方程中另一变量写成 该变量与第三变量平方和的正负平方根 2009年7月3日星期五 8 目录○ 上页 下页 返回
2009年7月3日星期五 8 目录 上页 下页 返回 C f y z = 0),(: o y x z ,( 0) 22 zxyf =+± 求旋转曲面方程时 ,平面曲线绕某坐标轴旋转 ,则该坐 标轴对应的变量不变 ,而曲线方程中另一变量写成 该变量与第三变量平方和的正负平方根. 思考:当曲线 C 绕 y 轴旋转时,方程如何?

例3试建立顶点在原点,旋转轴为z轴,半顶角为0 的圆锥面方程.(课本例4) 解:在y0z面上直线L的方程为 z=ycota 绕z轴旋转时,圆锥面的方程为 M(0,y,z) z=±√x2+y2cota 令a=cot 两边平方 z2=a2(x2+y2) 2009年7月3日星期五 9 目录○ 上页下页 (返回
2009年7月3日星期五 9 目录 上页 下页 返回 α 的圆锥面方程. (课本 例 4 ) 解 : 在yoz面上直线L 的方程为 z = y cot α 绕 z 轴旋转时,圆锥面的方程为 cot α 22 +±= yxz )( 2222 += yxaz 令 a = cot α x y z α 两边平方 L M y z),0( 例3 试建立顶点在原点, 旋转轴为z 轴, 半顶角为
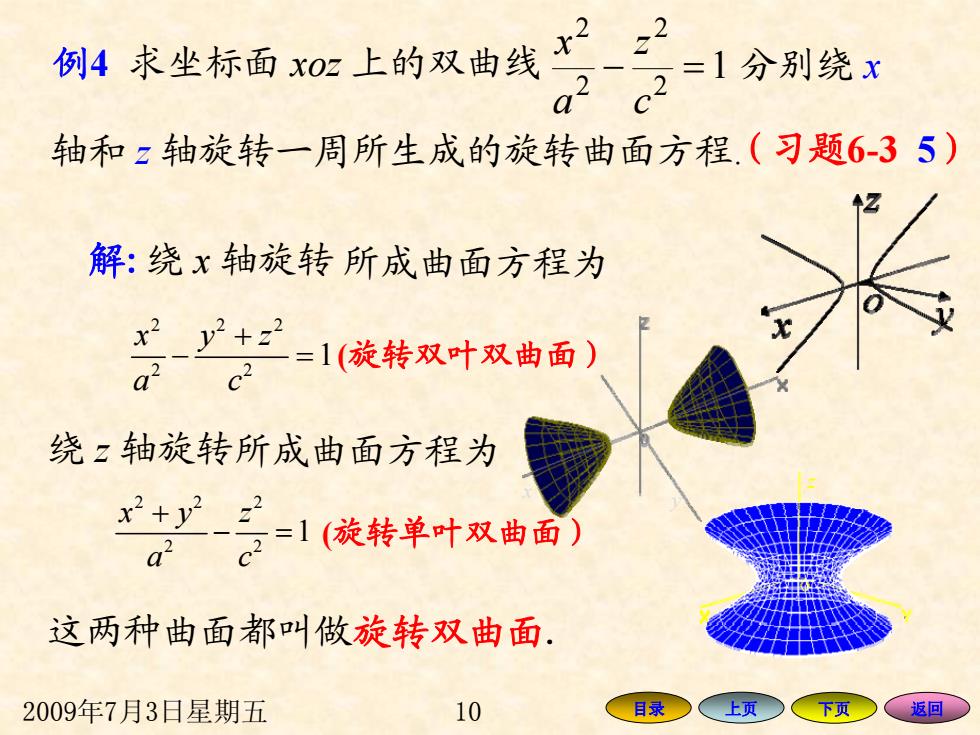
例4求坐标面x0上的双曲线 222 a22 =1分别绕x 轴和z轴旋转一周所生成的旋转曲面方程.(习题6-35) 解:绕x轴旋转所成曲面方程为 比广十1旋转双叶双曲面 a2 绕z轴旋转所成曲面方程为 1(旋转单叶双曲面 d 这两种曲面都叫做旋转双曲面. 2009年7月3日星期五 10 目录○ 上页>下页 返回
2009年7月3日星期五 10 目录 上页 下页 返回 x y 1 2 2 2 2 =− c z a x 分别绕 x 轴和 z 轴旋转一周所生成的旋转曲面方程. 解: 绕 x 轴旋转 2 22 2 2 1 x yz a c + − = 绕 z 轴旋转 222 2 2 1 xyz a c + − = 这两种曲面都叫做旋转双曲面. 所成曲面方程为 所成曲面方程为 z (旋转双叶双曲面) (旋转单叶双曲面) 例4 求坐标面 xoz 上的双曲线 (习题6-3 5 )