
第三章 第五节岛数的极值与最大值、最小值 Extremum Extremes of Function) 一、复习引入 二、极值的第一充分条件 三、极值的第二充分条件 四、最值问题 五、小结与思考练习 2009年7月3日星期五 1 目录○ 上页 返回
2009年7月3日星期五 1 目录 上页 下页 返回 第五节 函数的极值与最大值、最小值 第三章 四、最值问题 三、极值的第二充分条件 二、极值的第一充分条件 (Extremum & Extremes of Function) 一、复习引入 五、小结与思考练习

一、复习引入(Introduction) 1.极值定义设函数f(x)在区间(a,b)内有定义,x。是 (a,b)内的一点,如果存在x的一个邻域U(x),对于 U(x)内的任何,点x,有 f(x)≤f(x)或f(x)≥f(x), 则称f(x)是函数f(x)的一个极大值(或极小值),点x 是(x)的一个极大值点(或极小值,点),函数的极大值、 极小值统称为极值极大值,点与极小值点统称为极值点. 2.费马(Femat)引理如果函数f(x)在,点x,可导, 而且在点x取到极值,则f'(x)=0 2009年7月3日星期五 2 目录 上页 返回
2009年7月3日星期五 2 目录 上页 下页 返回 一、复习引入(Introduction) 1.极值定义 设函数 f ( ) x 在区间(,) a b 内有定义, 0 x 是 (,) a b 内的一点,如果存在 0 x 的一个邻域 0 U x( ),对于 0 U x( )内的任何点 x ,有 0 fx fx () ( ) ≤ 或 0 fx fx () ( ) ≥ , 则称 0 f ( ) x 是函数 f x( ) 的一个极大值(或极小值),点 0 x 是 f x( ) 的一个极大值点(或极小值点),函数的极大值、 极小值统称为极值.极大值点与极小值点统称为极值点. 2.费马(Femat)引理 如果函数 f x( )在点 0 x 可导, 而且在点 0 x 取到极值,则 0 f x ′( ) 0. =

由费马引理知,驻,点(Stagnation Point),即导数为 零的点是函数可能的极值点。 除驻点外函数还有没有其他的点是可能的极值,点? 在可能的极值,点中究竞那些点是极值点? 是极值,点时,是极大值点还是极小值,点呢? 研究极值到底有什么用?. 为此,这节课我们就来研究函数极值点的两个充分 条件,并在此基础上讨论最值问题! 2009年7月3日星期五 3 目录 上页 返回
2009年7月3日星期五 3 目录 上页 下页 返回 由费马引理知,驻点(Stagnation Point),即导数为 零的点是函数可能的极值点。 除驻点外函数还有没有其他的点是可能的极值点? 在可能的极值点中究竟哪些点是极值点? 是极值点时,是极大值点还是极小值点呢? 研究极值到底有什么用?. 为此,这节课我们就来研究函数极值点的两个充分 条件,并在此基础上讨论最值问题!

二、第一充分条件(The First Sufficient Condition) 定理1(第一充分条件)设函数f(x)在,点x,的某个邻 域U(x,6)内连续,在去心邻域U(x,6)内可导. (1)若x∈(x-6,x)时,f'(x)>0,(f'(x)0) 则函数f(x)在点x,处取得极大值;(极小值) (2)若x∈U(x,6)时,f'(x)的符号保持不变, 则,点x不是f(x)的极值点. 2009年7月3日星期五 4 目录 上页 返回
2009年7月3日星期五 4 目录 上页 下页 返回 二、第一充分条件(The First Sufficient Condition) 定理 1(第一充分条件) 设函数 f ( ) x 在点 0 x 的某个邻 域 0 U x( ,) δ 内连续,在去心邻域 o 0 U x( ,) δ 内可导. (1)若 0 0 x∈ − ( ,) x x δ 时, f x ′() 0 > , 而 0 0 x xx ∈ + (, ) δ 时, f x ′() 0 (极小值) (2)若 o 0 x Ux ∈ ( ,) δ 时, f ′( ) x 的符号保持不变, 则点 0 x 不是 f ( ) x 的极值点.
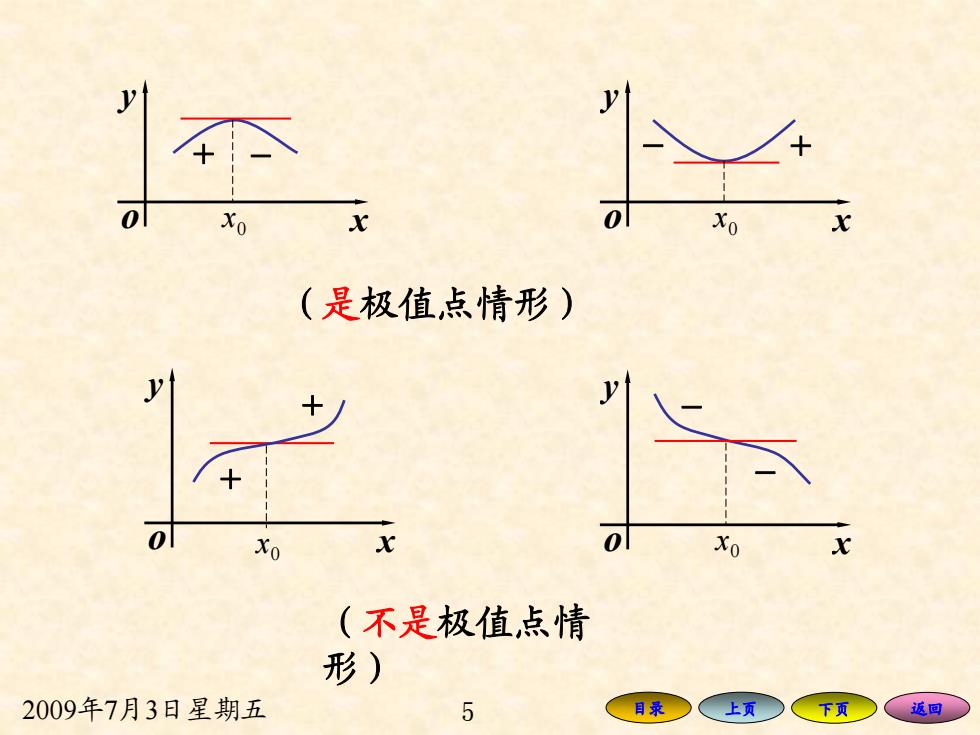
0 (是极值,点情形) Xo (不是极值,点情 形) 2009年7月3日星期五 5 上页 返回
2009年7月3日星期五 5 目录 上页 下页 返回 x y o x y x0 o 0 x + − − + (是极值点情形) x y o x y o 0 x 0 x + − − + (不是极值点情 形)

应当指出的是, 除驻,点是函数可能的极值,点外,导数不存在的,点 也可能是函数的极值点· 例如,对于函数f(x)=x|,我们曾经证明过它在 x=0处导数不存在,但(0,0)点显然是极值,点! 又如,对于函数f(x)=x3,y'(0)不存在. 因为当x≠0时y= 1 >0,故由第一充分条件知 3x2 x=0不是y=x的极值点 2009年7月3日星期五 6 目录 上页( 、返回
2009年7月3日星期五 6 目录 上页 下页 返回 应当指出的是, 除驻点是函数可能的极值点外,导数不存在的点 也可能是函数的极值点. 例如,对于函数 f () | | x x = ,我们曾经证明过它在 x = 0 处导数不存在,但(0,0) 点显然是极值点! 又如,对于函数 1 3 f ( ) x x = ,y′(0) 不存在. 因为当 x ≠ 0 时 3 2 1 0 3 y x ′ = > ,故由第一充分条件知 x = 0 不是 3 y x = 的极值点

根据上述讨论,我们可按下列步骤来求函数∫(x) 的极值点和相应极值: (1)求出导数f'(x),进而求出f(x)全部驻点或 导数不存在的,点; (2)考察f'(x)在各个驻点或导数不存在的点的 左、右邻域内符号的变化,判定该点是否为极值,点, 如果是极值点,进一步确定是极大值,点还是极小值 点; (3)求出f(x)的极值. 例1求函数f(x)=6x2-x3的极值.(老师讲解) 2009年7月3日星期五 7 目录 上页 返回
2009年7月3日星期五 7 目录 上页 下页 返回 我们可按下列步骤来求函数 f ( ) x 的极值点和相应极值: (1)求出导数 f ′( ), x 进而求出 f ( ) x 全部驻点或 导数不存在的点; (2)考察 f ′( ) x 在各个驻点或导数不存在的点的 左、右邻域内符号的变化,判定该点是否为极值点, 如果是极值点,进一步确定是极大值点还是极小值 点; 根据上述讨论, (3)求出 f ( ) x 的极值. 例 1 求函数 3 2 3 f () 6 x xx = − 的极值.(老师讲解)

例2设函数f(x)在(-o,+o)内 连续,其导函数的图形如右图所 示,试确定函数f(x)的极大值和 极小值点的个数.(课本例4) x,O/x 提示:(1)从图形可以看出, f'(x)=f'(x2)=f'(x3)=0 且在x=0处导数不存在。 (2)根据驻,点与导数不存在点左右两端的 符号确定是否极值,点。 答案:有(x,f(x)和(0,f(O》两个极大值,点; 有(x2,f(x2)和(x3,f(x3)两个极小值点。 2009年7月3日星期五 8 目录 上页 返回
2009年7月3日星期五 8 目录 上页 下页 返回 例 2 设函数 f ( ) x 在(,) −∞ +∞ 内 连续,其导函数的图形如右图所 示,试确定函数 f ( ) x 的极大值和 极小值点的个数.(课本例 4) 提示:(1)从图形可以看出, 123 fx fx fx ′() () () 0 = ′ ′ = = 且在 x = 0 处导数不存在。 (2) 根据驻点与导数不存在点左右两端的 符号确定是否极值点。 答案:有( ) 1 1 x ,() f x 和(0, (0)) f 两个极大值点; 有( ) 2 2 x ,() f x 和( x3 3 ,() f x ) 两个极小值点

三、第二充分条件(The Second Sufficient Condition) 定理2(第二充分条件)设函数f(x)在,点x,处具有 二阶导数,并且f'(x)=0,f"(x)≠0.则 (1)若当f"(x)0时,函数f(x)在点x,处取得极小值; 注1:本定理可利用极限的保号性加以证明; 注2:当"(x)=0时,本定理失效! 例如,函数f(x)=x3时,本定理失效! 2009年7月3日星期五 9 目录 上页 返回
2009年7月3日星期五 9 目录 上页 下页 返回 三、第二充分条件(The Second Sufficient Condition) 定理 2(第二充分条件) 设函数 f x( ) 在点 0 x 处具有 二阶导数,并且 0 f x ′()0 = , 0 f x ′′()0 ≠ .则 (1)若当 0 f x ′′()0 时,函数 f ( ) x 在点 0 x 处取得极小值; 注 1:本定理可利用极限的保号性加以证明; 注 2:当 0 f x ′′()0 = 时,本定理失效! 例如,函数 3 fx x ( ) = 时,本定理失效!

例3求函数f(x)=(x2-1)3+1的极值 解题思路: (课本例2) (1)求出f'(x),并求出f(x)全部驻点; (2)验证全部驻,点的二阶导数f"(x)是否为零。 如果驻点的二阶导数f"(x)不等于零,则利用第 二充分条件判定; 如果驻点的二阶导数∫"(x)等于零,此时,第二 充分条件失效,可利用第一充分条件判定。 2009年7月3日星期五 10 目录 上页 返回
2009年7月3日星期五 10 目录 上页 下页 返回 例 3 求函数 2 3 fx x ( ) ( 1) 1 = − + 的极值. 解题思路: (课本 例 2) (1)求出 f ′( ), x 并求出 f ( ) x 全部驻点; (2)验证全部驻点的二阶导数 f ′′( ) x 是否为零。 如果驻点的二阶导数 f ′′( ) x 不等于零,则利用第 二充分条件判定; 如果驻点的二阶导数 f ′′( ) x 等于零,此时,第二 充分条件失效,可利用第一充分条件判定