
第一章 第六节极限存在准则两个重要极限 Existence criterion for limits Two important limits) 一、极限存在的两个准则 二、两个重要极限 三、内容小结 2009年7月3日星期五 1 目录○ 上页 下页 、返回
2009年7月3日星期五 1 目录 上页 下页 返回 第六节 极限存在准则 两个重要极限 第一章 (Existence criterion for limits & Two important limits ) 二、两个重要极限 一、极限存在的两个准则 三、内容小结

1.单调有界准则 数列Xn:单调增加X1≤X2.≤尤n≤Xm+1≤., 单调减少X1≥X2.≥火m≥Xm+1≥., 准则I 单调有界数列必有极限 单调上升有上界数列必有极限 单调下降有下界数列必有极限 说明: ()在收敛数列的性质中曾证明:收敛的数列一定 有界,但有界的数列不一定收敛. (2)利用准则I来判定数列收敛必须同时满足数列 单调和有界这两个条件. 2009年7月3日星期五 2 目录 上页 下页 、返回
2009年7月3日星期五 2 目录 上页 下页 返回 1. 单调有界准则 数列 : n x , 单调增加 x ≤ x21 " ≤ x ≤ xnn + 1 ≤ " , 单调减少 x x21 " x xnn + 1 ≥≥≥≥ " 准则 I 单调有界数列必有极限 单调上升有上界数列必有极限 单调下降有下界数列必有极限 说 明 : (1) 在收敛数列的性质中曾证明:收敛的数列一定 有界,但有界的数列不一定收敛. (2) 利用准则Ⅰ来判定数列收敛必须同时满足 数列 单调 和有界这两个条件.

(③)准则I只能判定数列极限的存在性,而未给出 求极限的方法 例如,数列xn=(-)”,虽然有界但不单调; 数列xn=n,虽然是单调的,但其无界, 易知,这两数列均发散 (④)对于准则I,函数极限根据自变量的不同变化过程 (x→x,x→x,x→-0,x→-0,x→+0)也有类似的 准则,只是准则形式上略有不同.例如, 准则'设函数f(x)在,点x,的某个左邻域内单调 并且有界,则f(x)在x的左极限f(x。)必存在. 2009年7月3日星期五 3 目录 上页 下页 返回
2009年7月3日星期五 3 目录 上页 下页 返回 (3) 准则Ⅰ只能判定数列极限的存在性,而未给出 求极限的方法. ( 1) n n x = − n x = n 例如,数列 ,虽然有界但不单调; 数列 ,虽然是单调的,但其无界, 易知,这两数列均发散. (4) 对于准则 I,函数极限根据自变量的不同变化过程 0 ( , x x → − 0 x x , → + x → −∞, x → −∞, x → +∞ ) 也有类似的 准则,只是准则形式上略有不同. 例如, 准则 I′ 设函数 f ( ) x 0 f ( ) x x 0 x 0 f ( ) x − 在点 的某个左邻域内单调 并且有界,则 在 的左极限 必存在.

作为准则I的应用,我们讨论一个重要极限: m+=? 首先,证x+ 是单调的。 +-+++日 1+n n+1 所以,数列,1+是单调增加的。 2009年7月3日星期五 目录 上页 下页 返回
2009年7月3日星期五 4 目录 上页 下页 返回 作为准则Ⅰ的应用,我们讨论一个重要极限: 1 lim 1 ? n n→∞ n ⎛ ⎞ ⎜ ⎟ + = ⎝ ⎠ 1 1 n n x n ⎛ ⎞ = + ⎜ ⎟ ⎝ ⎠ 1 1 n n x n ⎛ ⎞ = + ⎜ ⎟ ⎝ ⎠ 1 1 1 n n ⎛ ⎞ ⋅⎜ ⎟ + ⎝ ⎠ 首先,证 是单调的. = 11 1 11 1 1 nn n ⎛ ⎞⎛ ⎞ ⎛ ⎞ =⋅ + ⋅ + + ⎜ ⎟⎜ ⎟ ⎜ ⎟ ⎝ ⎠⎝ ⎠ ⎝ ⎠ " 1 1 1 1 1 2 1 1 n n n n n n n + + ⎡ ⎛ ⎞ ⎤ ⎢ + + ⎜ ⎟⎥ ⎝ ⎠ ⎛ ⎞ + ≤ = ⎢ ⎥ ⎜ ⎟ ⎢ + + ⎥ ⎝ ⎠ ⎢ ⎥ ⎣ ⎦ 1 1 1 1 1 n n x n + + ⎛ ⎞ ⎜ ⎟ + = ⎝ ⎠ + = 1 1 n n x n ⎛ ⎞ = + ⎜ ⎟ ⎝ ⎠ 所以,数列 是单调增加的.

其次,证-+ 有界.显然,xn≥x,=2 类似子x-〔+日单调性的证明可证得教列,〔- 是单调增加的。设数列+,则 由于数列yn是单调增加的,所以数列n是单调减少的 又x(1++ =2m≤31=4 则2≤x,<4.综上,根据极限存在准则I可知,数列是 收敛的. 2009年7月3日星期五 5 目录 上页 下页 返回
2009年7月3日星期五 5 目录 上页 下页 返回 1 1 n n x n ⎛ ⎞ = + ⎜ ⎟ ⎝ ⎠ 1 2 n x x ≥ = 1 1 n n y n ⎛ ⎞ = − ⎜ ⎟ 1 ⎝ ⎠ 1 1 n n z n + ⎛ ⎞ = + ⎜ ⎟ ⎝ ⎠ 1 1 1 n n z n + ⎛ ⎞ = + ⎜ ⎟ ⎝ ⎠ = 1 1 1 1 1 1 11 1 1 1 1 n n n n n n y n n n + + + + ⎛ ⎞ + ⎜ ⎟ == = ⎝ ⎠ ⎛⎞⎛ ⎞ ⎜⎟⎜ ⎟ − ⎝⎠⎝ ⎠ + + n y n z 显然, 单调性的证明可证得数列 是单调增加的.设数列 由于数列 是单调增加的,所以数列 是单调减少的 . 又 1 1 n n x n ⎛ ⎞ = + ⎜ ⎟ ⎝ ⎠ 其次,证 有界. 类似于 ,则 1 1 1 1 11 4 n n n n x z z n n + ⎛ ⎞⎛ ⎞ = ⎜ ⎟⎜ ⎟ + <+ =≤= ⎝ ⎠⎝ ⎠ 2 4 n 则 ≤ x < . 综上,根据极限存在准则Ⅰ可知,数列是 收敛的

通常用字母e来表示这个极限,即 +=ee-27Ias- 也可以证明,当X取实数而趋于+0或-0时,函数 的极及都存在且事等于8,即四1+=。 利用变量代换,可得更一般的形式 lim [1+a(xe a(x)→0 2009年7月3日星期五 6 目录 上页 下页 返回
2009年7月3日星期五 6 目录 上页 下页 返回 e 1 lim 1 e n n→∞ n ⎛ ⎞ ⎜ ⎟ + = ⎝ ⎠ 通常用字母 来表示这个极限,即 x +∞ − ∞ y = 1 1 x x ⎛ ⎞ ⎜ ⎟ + ⎝ ⎠ e 1 lim 1 e x x→∞ x ⎛ ⎞ ⎜ ⎟ + = ⎝ ⎠ 也可以证明,当 取实数而趋于 或 时,函数 的极限都存在且都等于 ,即 [ ] 1 0 ( ) ) lim 1 ( ) x e x x α α α → + = ( (e 2.71828 ) = " 利用变量代换,可得更一般的形式

1求1 年。 X一2 2求一1 - =e3 2009年7月3日星期五 7 目录 上页 下页 返回
2009年7月3日星期五 7 目录 上页 下页 返回 例 1 2 1 lim 1 . x x→∞ x ⎛ ⎞ ⎜ ⎟ − ⎝ ⎠ 求 解 : 2 1 lim 1 x x x − − →∞ ⎡ ⎤ ⎛ ⎞ = + ⎢ ⎥ ⎜ ⎟ ⎢ ⎥ ⎝ ⎠ ⎦ − ⎣ ( 2) 1 lim 1 x x x ⋅ − →∞ − ⎛ ⎞ = + ⎜ ⎟ ⎝ ⎠ − 原式 2 e . − = 例2 求 1 0 lim 1 3 x x x → ⎛ ⎞ ⎜ ⎟ − ⎝ ⎠ 解 : 1 3 1 3 0 0 lim 1 lim 1 3 3 x x x x x x ⎛ ⎞ ⎜ ⎟ − − ⎝ ⎠ → → ⎛⎞ ⎛ ⎞ − ⎜⎟ ⎜ ⎟ −= + ⎝⎠ ⎝ ⎠ i 1 3 3 0 lim 1 3 x x x − − → ⎡ ⎤ ⎛ ⎞ − = + ⎢ ⎥ ⎜ ⎟ ⎢ ⎥ ⎝ ⎠ ⎣ ⎦ 1 3 e − =

2.夹逼准则 雅则Ⅲ0%≤≤m2 (2)lim yn=lim zn=a ◆lim=a n->oo n->oo 证:由条件(2),H6>0,3N1,W2, 当n>N1时,yn-aN2时,n-aN时,有 a-8<yn<a+8,a-ε<2n<a+8, 由条件(1)a-8<yn≤Xn≤2n<a+8 即xn-a<6,故limn=a. n-→0 2009年7月3日星期五 8 目录→ (上页 下页 返回
2009年7月3日星期五 8 目录 上页 下页 返回 2. 夹逼准则 准则II y z a n n n n = = → ∞ → ∞ lim)2( lim )1( y ≤ x ≤ z n = "),2,1( nnn axn n = → ∞ lim ⎭ ⎬ ⎫ 证: 由条件 (2) , ∀ ε > ,0 , ∃ N1 当 N1 n > 时 , − ay 时 , − az N 时, 有 a − ε < y < a + ε , n a − ε < z < a + ε , n 由条件 (1) nnn a − ε < y ≤ x ≤ z < a + ε 即 − ax < ε , n 故 x n a .limn = → ∞ , N2

我们可将准则推广到函数的情形: 准则'当x∈Uxo,δ)时,g(x)≤f(x)≤h(x),且 (x>X>0) lim g(x)=lim h(x)=4 x→x0 x→X0 (x-→0) (x-→∞) lim f(x)=4 x→X0 (x→0) 准则和准则'统称为夹逼准则. 注意:利用夹逼准则求极限关键是构造出y与2n, 并且ym与2n的极限是容易求的. 2009年7月3日星期五 9 目录 上页 下页 返回
2009年7月3日星期五 9 目录 上页 下页 返回 我们可将准则II推广到函数的情形: 准则II ′ ,),( 当 xx 0 δ 时 D ∈ ∪ g Axhx xx xx = = → → )(lim)(lim0 0 g x ≤ f x)( ≤ xh ,)()( f Ax xx = → )(lim0 ( 0) x X > > ( ) x → ∞ ( ) x → ∞ ( ) x → ∞ 且 注意 : 准则II和准则II′统称为夹逼准则 . . , 与并且 的极限是容易求的 利用夹逼准则求极限关键是构造出 y n 与 n y n z n z
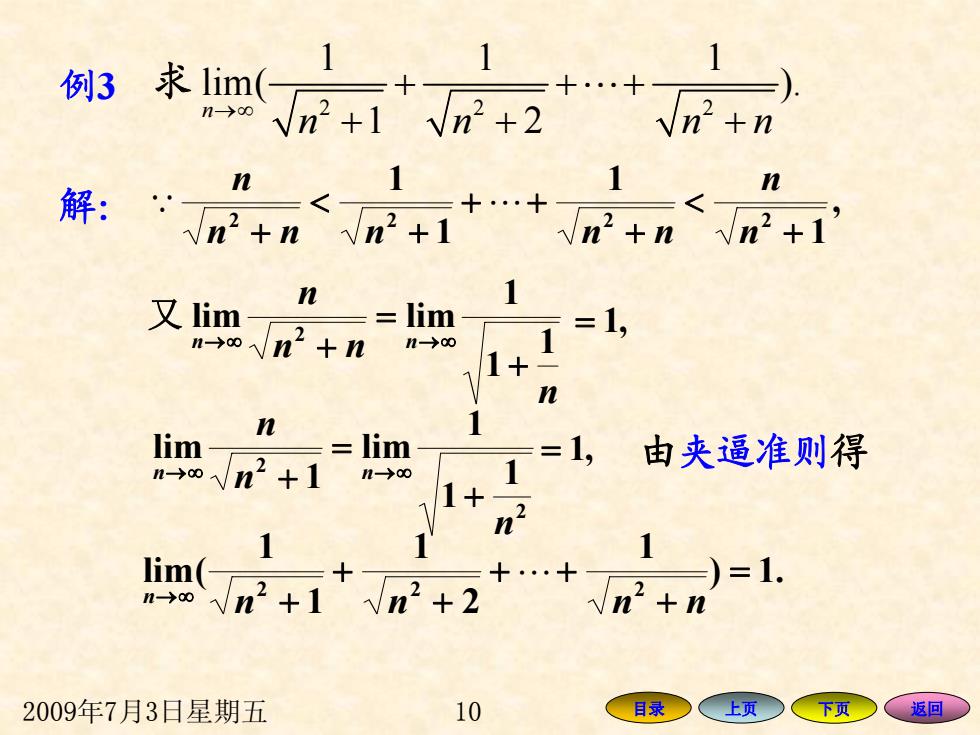
例3求lim( n2+i√n2+2n2+n 解:“r+n n 1 1 n m+++2+n+ 又lim n -lim =1, n-→ooVn2+nn→o 1+ n lim- =lim n-→oVn2+1n-→ 1, 由夹逼准则得 1 lim( 十十 →oVn2+1n2+2 1-)=1. n +n 2009年7月3日星期五 10 目录 上页 下页 返回
2009年7月3日星期五 10 目录 上页 下页 返回 例 3 22 2 11 1 lim( ). 1 2 n n n nn →∞ + ++ ++ + 求 " 解: , 1 1 1 1 2 2 2 2 + < + ++ + < + n n nnn nn n ∵ " n nn n n n 1 1 1 lim 2 lim + = ∞→ + ∞→ 又 = ,1 2 2 1 1 1 lim 1 lim n n n n n + = ∞→ + ∞→ = ,1 由夹逼准则 得 .1) 1 2 1 1 1 (lim 2 2 2 = + ++ + + n ∞→ + nn nn