
数学模型 第七章 差分方程模型 7.1市场经济中的蛛网模型 7.2减肥计划—节食与运动 7.3差分形式的阻滞增长模型 7.4按年龄分组的种群增长
7.1 市场经济中的蛛网模型 7.2 减肥计划——节食与运动 7.3 差分形式的阻滞增长模型 7.4 按年龄分组的种群增长 第七章 差分方程模型
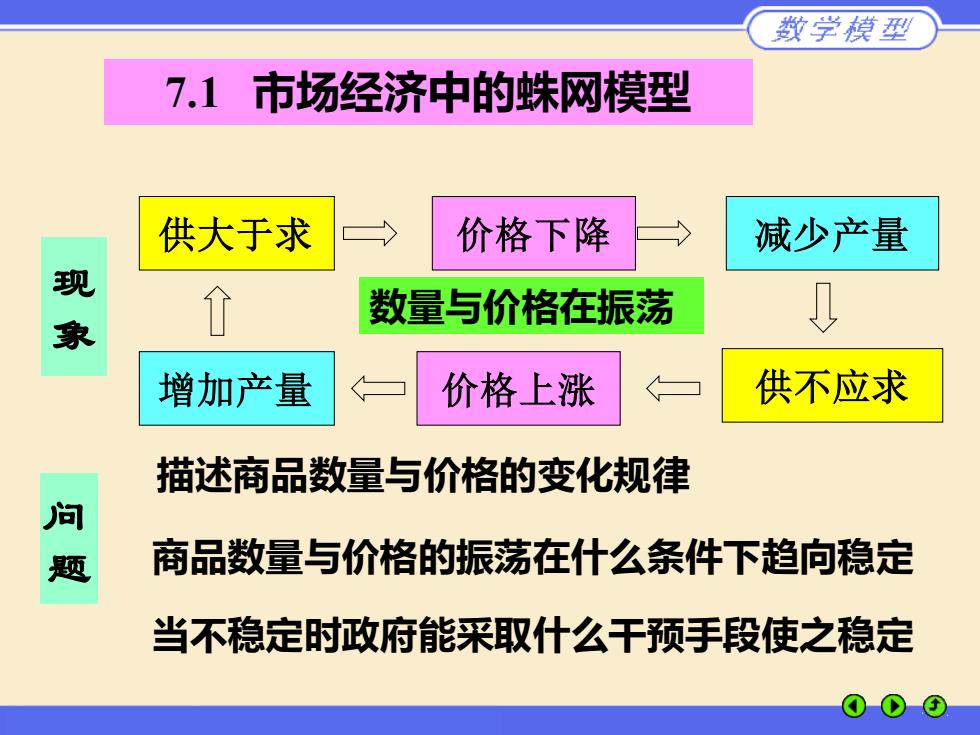
致学模型 7.1市场经济中的蛛网模型 供大于求 价格下降 减少产量 现 数量与价格在振荡 象 增加产量 价格上涨 供不应求 描述商品数量与价格的变化规律 问 题 商品数量与价格的振荡在什么条件下趋向稳定 当不稳定时政府能采取什么干预手段使之稳定
7.1 市场经济中的蛛网模型 问 题 供大于求 现 象 商品数量与价格的振荡在什么条件下趋向稳定 当不稳定时政府能采取什么干预手段使之稳定 价格下降 减少产量 增加产量 价格上涨 供不应求 描述商品数量与价格的变化规律 数量与价格在振荡
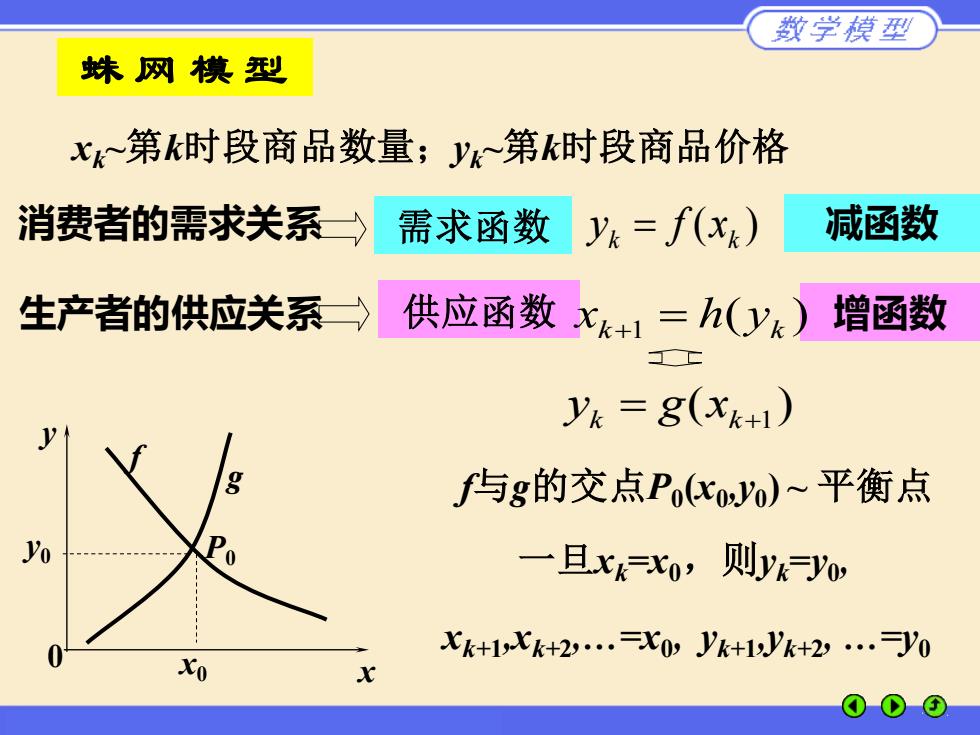
数学模型 蛛网模型 x~第k时段商品数量;y~第k时段商品价格 消费者的需求关系> 需求函数 y=f(x) 减函数 生产者的供应关系) 供应函数 x+=h() 增函数 yk=8(Xk+1) g 与g的交点Pco)~平衡点 Yo 一且x=,则yyo Xk+1Xk+2.X0 k+12Vk+2.0 Xo x
蛛 网 模 型 g x0 y0 P0 f x y 0 xk~第k时段商品数量;yk~第k时段商品价格 消费者的需求关系 ( ) k k y = f x 生产者的供应关系 减函数 供应函数 增函数 需求函数 f与g的交点P0 (x0 ,y0 ) ~ 平衡点 一旦xk=x0,则yk=y0 , xk+1 ,xk+2 ,.=x0 , yk+1 ,yk+2 , .=y0 ( ) k 1 k x = h y + ( ) k = k+1 y g x
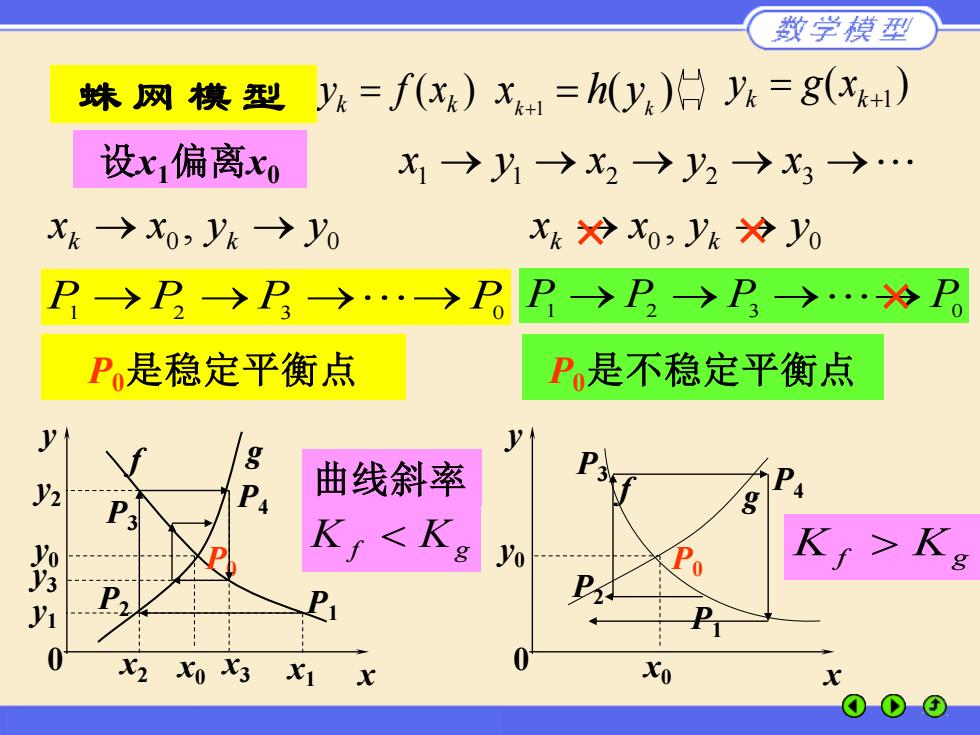
数学模型 蛛网模型 yx=f(xg)x=h(y)y=g(x) 设x偏离x0 X1→y1→X2→y2→X3→. xk→X0,yk)y0 xk冷Xo,yk冷y0 P→P→P>→PP→P→P→.冷P P是稳定平衡点 P是不稳定平衡点 g D V2 曲线斜率 P KI>K P. P 2X03 X1 x 0
x y 0 f g y0 x0 P0 设x1偏离x0 x1 x2 y P2 1 P1 y2 P3 P4 x3 y3 x1 → y1 → x2 → y2 → x3 → P1 → P2 → P3 →→ P0 0 0 x x , y y k → k → P0是稳定平衡点 P1 P2 P3 P4 P0是不稳定平衡点 K f Kg x y 0 y0 x0 P0 f g ( ) k k y = f x ( ) k 1 k x = h y + ( ) k = k+1 y g x 0 0 x x , y y k → k → K f Kg 曲线斜率 蛛 网 模 型 P1 → P2 → P3 →→ P0

数学模型 方程模型 在P点附近用直线近似曲线 %=f(x) yk-y=-a(xk-x)(@>0) xk+=h(yk)1-x0=B(yk-yo)(B>0) X1-x三-Cfx-x) x+1-x。=(-β)(x,-x)》 aB1 (a>1/B)x →00 P不稳定 Ki>Kg 方程模型与蛛网模型的一致 a=K 1/B=K
( ) k k y = f x ( ) k 1 k x = h y + 在P0点附近用直线近似曲线 ( ) ( 0) yk − y0 = − xk − x0 ( ) ( 0) xk+1 − x0 = yk − y0 ( ) 1 0 0 x x x x k + − = − k − ( ) ( ) 1 0 1 0 x x x x k k + − = − − 1 P0稳定 P0不稳定 0 x x k → xk → = K f = Kg 1/ ( 1/ ) ( 1/ ) 1 方 程 模 型 K f Kg K f Kg 方程模型与蛛网模型的一致

致学模型 结果解释 考察a,B的含义 x一第k时段商品数量;y一第k时段商品价格 yk-yo=-a(xk-xo) α~商品数量减少1单位,价格上涨幅度 Xk+1-Xo=B(yk-yo) B~价格上涨1单位,下时段)供应的增量 α~消费者对需求的敏感程度 a小,有利于经济稳定 B~生产者对价格的敏感程度 B小,有利于经济稳定 0B<1经济稳定
( ) 0 0 y y x x k − = − k − ~ 商品数量减少1单位, 价格上涨幅度 ( ) 1 0 0 x x y y k+ − = k − ~ 价格上涨1单位, (下时段)供应的增量 考察 , 的含义 ~ 消费者对需求的敏感程度 ~ 生产者对价格的敏感程度 小, 有利于经济稳定 小, 有利于经济稳定 结果解释 xk~第k时段商品数量;yk~第k时段商品价格 1 经济稳定 结果解释
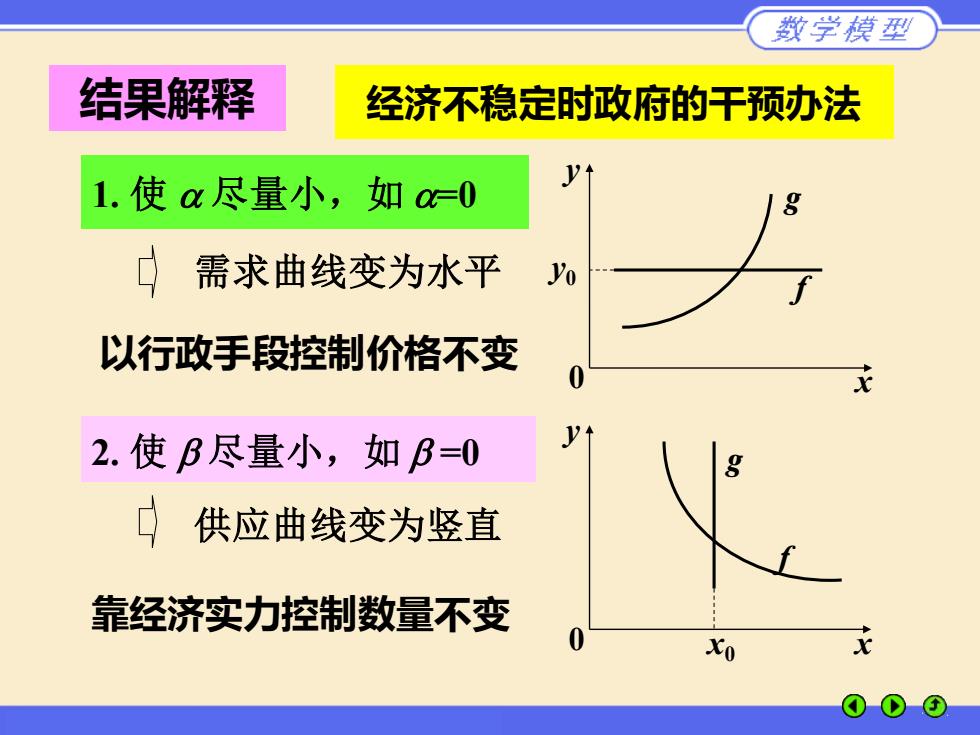
数学模型 结果解释 经济不稳定时政府的干预办法 1.使ax尽量小,如=0 需求曲线变为水平 Yo 以行政手段控制价格不变 2.使B尽量小,如B=0 口供应曲线变为竖直 靠经济实力控制数量不变
经济不稳定时政府的干预办法 1. 使 尽量小,如 =0 以行政手段控制价格不变 2. 使 尽量小,如 =0 靠经济实力控制数量不变 x y 0 y0 g f x y 0 x0 g f 结果解释 需求曲线变为水平 供应曲线变为竖直

数学模型 模型的推广 生产者管理水平提高 X=h(Yk) ·生产者根据当前时段和前一时 段的价格决定下一时段的产量。 设供应函数为 -x,=F[y+y)/2-y,] 需求函数不变 y-。=-0(x-x)》 2x+2+041+0x。=2(1+0B)x,k=1,2,. 二阶线性常系数差分方程 x为平衡点 研究平衡点稳定,即k→0,xkx的条件
[( )/ 2 ] 1 0 1 0 x x y y y k+ − = k + k− − 模型的推广 • 生产者根据当前时段和前一时 段的价格决定下一时段的产量。 ( ) 0 0 y y x x k − = − k − 生产者管理水平提高 设供应函数为 需求函数不变 2xk+2 +xk+1 +xk = 2(1+)x0 , k =1,2, 二阶线性常系数差分方程 x0为平衡点 研究平衡点稳定,即k→, xk→x0的条件 ( ) k 1 k x = h y + + = − + 2 1 1 k k k y y x h

数学模型 模型的推广 2x+2+0x+1+o=2(1+0P)x 方程通解x=C,2+c2入欢(C1,c2由初始条件确定) 1,2特征根,即方程222+B2+B=0的根 平衡点稳定,即k→o,x→x的条件:入.2<1 1,=-a0±ap-8a0 邛 4 =12 平衡点稳定条件0B<2 比原来的条件B<1放宽了
4 ( ) 8 2 1,2 − − = 2 1 0 2x x x 2(1 )x k+ + k+ + k = + 方程通解 k k xk = c1 1 + c2 2 (c1 , c2由初始条件确定) 1, 2~特征根,即方程 2 0 的根 2 + + = 平衡点稳定,即k→, xk→x0的条件: 1,2 1 平衡点稳定条件 2 比原来的条件 1 放宽了 2 1,2 = 模型的推广

数学模型 7.2减肥计划 节食与运动 ·体重指数BM=wkg)/(m2).18.525~超重;BM>30~肥胖, 景 ·多数减肥食品达不到减肥目标,或不能维持 ·通过控制饮食和适当的运动,在不伤害身体 的前提下,达到减轻体重并维持下去的目标 分 ·体重变化由体内能量守恒破坏引起 ·饮食(吸收热量)引起体重增加 ·代谢和运动(消耗热量)引起体重减少
7.2 减肥计划——节食与运动 背 景 • 多数减肥食品达不到减肥目标,或不能维持 • 通过控制饮食和适当的运动,在不伤害身体 的前提下,达到减轻体重并维持下去的目标 分 析 • 体重变化由体内能量守恒破坏引起 • 饮食(吸收热量)引起体重增加 • 代谢和运动(消耗热量)引起体重减少 • 体重指数BMI=w(kg)/l 2 (m2 ). 18.525 ~ 超重; BMI>30 ~ 肥胖