
上次课内容复习: 向径的基本分解式r=xi+yⅵ+k. ■向量的坐标 向量的基本分解式a=axi+ayj+azk 。向量模的坐标表示ld=√a+a+a ·向量的运算及其坐标之间的数量运算关系 ■两向量平行的充分必要条件 ·向量的数量积及其夹角余弦的坐标表示、两向量 垂直的充分必要条件、向量的方向余弦
上次课内容复习: ◼ 向量的坐标 ◼ 向量模的坐标表示 ◼ 向量的运算及其坐标之间的数量运算关系 ◼ 两向量平行的充分必要条件 ◼ 向量的数量积及其夹角余弦的坐标表示、两向量 垂直的充分必要条件、向量的方向余弦 向径的基本分解式 向量的基本分解式 r = x i +y j +z k. x = a i y +a j z a +a k a 222 x y z = + + aaa

§6.3平面及其方程 由中学立体几何知:确定一张平面的条件有: (1)经过空间一点且与一已知直线垂直; (2)经过空间不在一条直线上的三点; (3)经过空间两条相交的直线
§6.3 平面及其方程 由中学立体几何知:确定一张平面的条件有: (1)经过空间一点且与一已知直线垂直; (2)经过空间不在一条直线上的三点; (3)经过空间两条相交的直线
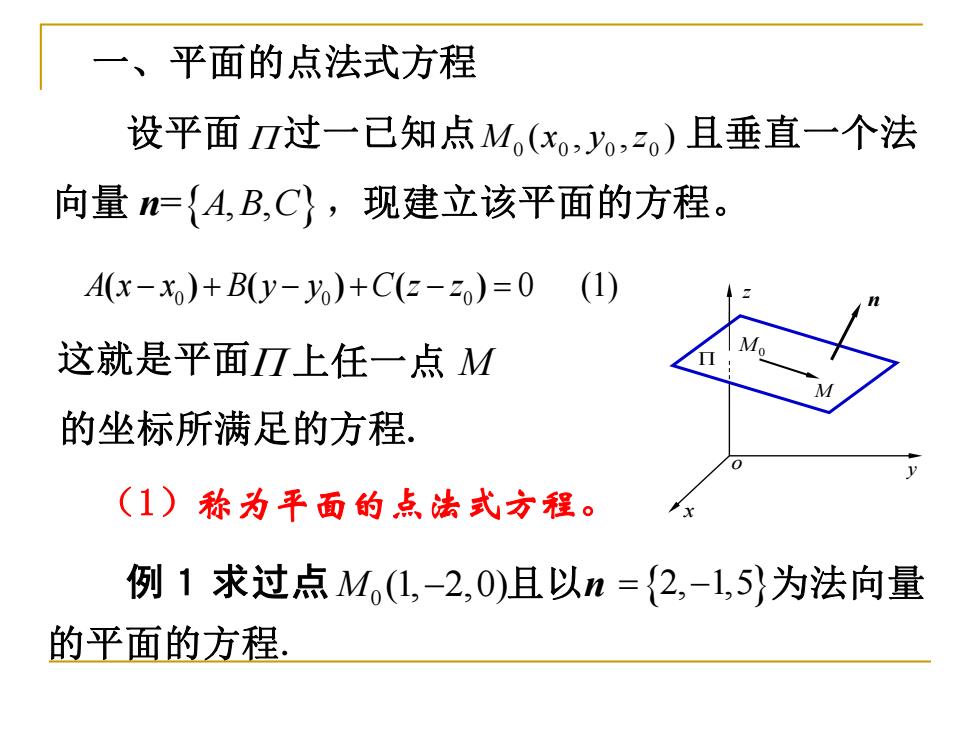
一、平面的点法式方程 设平面7过一已知点M(,)且垂直一个法 向量={A,B,C},现建立该平面的方程。 A(x-x)+By-%)+C(2-)=0(1) 这就是平面I上任一点M 的坐标所满足的方程. (1)称为平面的点法式方程。 例1求过点M(L,-2,0)且以n={2,-1,5}为法向量 的平面的方程
一、平面的点法式方程 设平面 过一已知点 且垂直一个法 向量 n= ,现建立该平面的方程。 ( , , ) 0 0 0 0 M x y z A B C , , x z y o M0 M 0 0 0 n A x x B y y C z z ( ) ( ) ( ) − + − + − = 0 (1) 这就是平面 上任一点 M 的坐标所满足的方程. (1)称为平面的点法式方程。 的平面的方程. 例1 求过点 0 M (1, 2,0) − 且以n = − 2, 1,5 为法向量

例2求过三点M,(1,1,1),M2(-3,2,1),M3(4,3,2) 的平面方程. 两点说明: (1)若n是平面Ⅱ一个法向量,则n(2≠0)也是 该平面的法向量。 (2)在解一个包含三个未知数、两个方程的方程 组时,首先确定一个未知数的值,另外两个未知数即 可解得
例2 求过三点 1 M ( , , ), 111 2 M ( , , ), −3 2 1 (4,3,2) M3 的平面方程. 两点说明: (2)在解一个包含三个未知数、两个方程的方程 组时,首先确定一个未知数的值,另外两个未知数即 可解得。 (1)若n是平面 一个法向量,则 也是 该平面的法向量。 n( ) 0

二、平面的一般方程 平面的点法式方程是三元一次方程,由于任一平 面都可以用它上面的一点及其法线向量来确定,所以 任何一个平面都可以用三元一次方程来表示。 反过来,设有三元一次方程 Ax+By+Cz+D=0 (2) 任取满足方程(2)的一组数xoyo、。,即 Ax+By+C2。+D=0(3) (2)-(3) A(x-x)+B(y-o)+C(z-Z0)=0 (4)
二、平面的一般方程 平面的点法式方程是三元一次方程,由于任一平 面都可以用它上面的一点及其法线向量来确定,所以 任何一个平面都可以用三元一次方程来表示。 反过来,设有三元一次方程 Ax By Cz D + + + = 0 (2) (2) (3) − 0 0 0 A x x B y y C z z ( ) ( ) ( ) 0 (4) − + − + − = 0 0 0 x 、y 、z 0 0 0 Ax By Cz D + + + = 0 (3) 任取满足方程(2)的一组数 ,即

根据系数的特殊取值,归纳其图形特点如下: 当D=0时,方程(2)成为Ax+By+Cz=0,它 表示一个经过原点的平面; 当C=0时,方程(2)成为Ax+By+D=0,它 表示一个与z轴平行的平面; 当B=C=0,方程(2)成为Ax+D=0,它表 示一个平行于yOz面的平面; 当C=D=0,方程(2)成为Ax+By=0,它表 示一个经过z轴的平面
根据系数的特殊取值,归纳其图形特点如下: D = 0 时,方程(2)成为 Ax By Cz + + = 0 表示一个经过原点的平面; 当 ,它 C = 0 时,方程(2)成为 Ax By D + + = 0 表示一个与 z 轴平行的平面; 当 ,它 当 B = C = 0 ,方程(2)成为 Ax + D = 0 示一个平行于 yOz 面的平面; ,它表 当 C = D = 0 ,方程(2)成为 Ax + By = 0 ,它表 示一个经过 z 轴的平面

例3一个平面通过x轴和点(3,1,-1),求该平面的 方程。 例4 求过三点P(a,0,0)、Q(0,b,0)、R(0,0,c) 的平面的方程(其中a、b、c为不等于零的常数)。 x+业+2=1 (5) a b 方程(5)叫做平面的载距式方程, a、b、C依次叫做平面在x、y2 轴上的载距
例3 一个平面通过 x 轴和点 (3,1,−1) , 求该平面的 方程。 例4 求过三点 P(a,0,0) 、 Q(0,b,0) 、 R(0,0,c) 的平面的方程(其中 a、b、c 为不等于零的常数)。 z x y o R P Q + + =1 (5) x y z a b c 方程(5)叫做平面的截距式方程, a、b、c 依次叫做平面在 x、y、z 轴上的截距
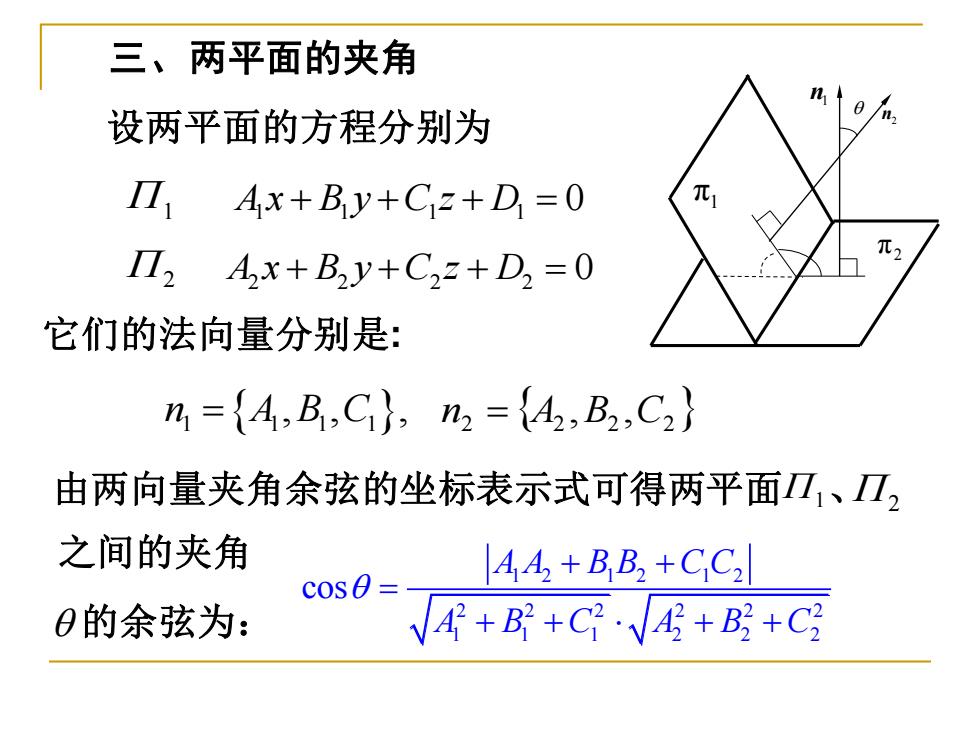
三、两平面的夹角 设两平面的方程分别为 17 Ax+By+C=+D=0 I2A,x+B2y+C22+D2=0 它们的法向量分别是: h={A,B,C},n2={A2,B2,C2} 由两向量夹角余弦的坐标表示式可得两平面Ⅱ1、I, 之间的夹角 44+BB2+CC2 cos0= 0的余弦为: +B2+C2+B+C2
三、两平面的夹角 1 1 1 1 1 A x B y C z D + + + = 0 2 2 2 2 2 A x B y C z D + + + = 0 设两平面的方程分别为 n A B C 1 1 1 1 = , , , n2 = A2 ,B2 ,C2 它们的法向量分别是: n1 n2 1 π 2 π 由两向量夹角余弦的坐标表示式可得两平面 1 、 2 之间的夹角 的余弦为: 1 2 1 2 1 2 2 2 2 2 2 2 1 1 1 2 2 2 cos A A B B C C A B C A B C + + = + + + +

从两向量垂直、平行的条件可得如下结论: Ⅱ,Ⅱ,互相垂直的充分必要条件是: 44+BB2 +C C2=0 I,几,互相平行的充分必要条件是: 4-B-C B,C, 例5求两平面x-y+2z=6和2x+y+z-5=0 的夹角
从两向量垂直、平行的条件可得如下结论: 1 2 , 互相垂直的充分必要条件是 : A1 A2 + B1 B2 +C1 C2 = 0 例5 求两平面 x − y + 2z = 6 和 2x + y + z − 5 = 0 的夹角. 2 2 1 2 1 2 1 C C B B A A = = 1 , 互相平行的充分必要条件是 :

例6设P(xo,yo,2o)是平面Ax+By+Cz+D=0 外的一点,求P。到这平面的距离。 P d=[Axo+B+Czo+Dl A+B2+D2 本次课小结: (1)熟练掌握平面的点法式方程、平面的一般方 程、平面的截距式方程。 (2)熟练掌握两平面夹角的余弦公式,熟练掌握 两平面相互垂直、平行的充要条件
例6 设 ( , , ) 0 0 0 0 P x y z 是平面 Ax By Cz D + + + = 0 外的一点,求 P0 到这平面的距离。 n P0 P1 0 0 0 2 2 2 + + + = + + Ax By Cz D d A B D 本次课小结: (1)熟练掌握平面的点法式方程、平面的一般方 程、平面的截距式方程。 (2)熟练掌握两平面夹角的余弦公式,熟练掌握 两平面相互垂直、平行的充要条件