
§9.5函数展开成幂级数 两类问题:在收敛域内 00 幂级数∑anx” 求和 和函数S(x) n=0 展开 本节内容: 一、泰勒(Taylor)公式 二、泰勒(Taylor)级数 三、函数展开成幂级数
两类问题:在收敛域内 和函数 求 和 展 开 本节内容: 一、泰勒 ( Taylor ) 公式 三、函数展开成幂级数 §9.5 函数展开成幂级数 二、泰勒 ( Taylor ) 级数

一、泰勒(Taylor)公式 为了研究一个给定函数是否可以表示成为一个幂 级数的问题,我们首先讨论一个给定函数是否可以近 似表示成为一个多项式的问题. 考察任一n次多项式 Pn(x)=a+a41(x-xo)+a2(x-x)2+.+an(x-xo)”(1) a=n.a=,4=,a,=P 21 多项式p(x)的各项系数由其在点x的各阶导数 值所唯一确定
一、 泰勒(Taylor)公式 为了研究一个给定函数是否可以表示成为一个幂 级数的问题,我们首先讨论一个给定函数是否可以近 似表示成为一个多项式的问题. 考察任一n次多项式 2 0 1 0 2 0 0 ( ) ( ) ( ) ( )n n n p x a a x x a x x a x x = + − + − + + − (1) ( 0 0 0 0 0 1 2 ( ) ( ) ( ) ( ), , , , 1! 2! ! = = = = n) n n n n n p x p x p x a p x a a a n 多项式 p x n ( ) 的各项系数由其在点 x0 的各阶导数 值所唯一确定

对于一般函数f(x),设它在点x处存在直到n 阶的导数,由这些导数构造一个次多项式: Tc-) (2) ++fm((x-x (2)式称为函数f(x)在点x处的泰勒多项式, 其中各项系数(k=0,12,)称为泰勒系数. k! f(x)=Tn(xo),k=0,1,2,.,n
0 0 2 0 0 0 ( ) 0 0 ( ) ( ) ( ) ( ) ( ) ( ) 1! 2! ( ) ( ) ! n n n f x f x T x f x x x x x f x x x n = + − + − + + − (2) (2)式称为函数 f x( ) 在点 x0 处的泰勒多项式, ( ) 0 ( ) ( 0 1,2 , ) ! k f x k n k 其中各项系数 = , , 称为泰勒系数. ( ) 0 0 ( ) ( ), 0,1,2, , k n f x T x k n = = 对于一般函数 ,设它在点 处存在直到n 阶的导数,由这些导数构造一个次多项式 : f x( ) 0 x

定理1(泰勒(Taylor)中值定理)设函数f(x)在 [a,b]上存在直至n阶的连续导函数,在(a,b)内存在 (n+)阶导函数,则对任意的x,x∈[a,b],至少存在 一点5∈(a,b),使得 -)fx)-+G) 21 (%(x-x+R(x) 其中 5是介于x,与x (4) (n+1)! 之间的某个值
定理1(泰勒(Taylor)中值定理) 设函数 f (x) 在 a b, n (a b, ) (n +1) x x a b , , 0 (a b, ) 上存在直至 阶的连续导函数,在 阶导函数,则对任意的 ,使得 内存在 ,至少存在 一点 0 0 2 0 0 0 ( ) 0 0 ( ) ( ) ( ) ( ) ( ) ( ) 1! 2! ( ) ( ) ( ) ! n n n f x f x f x f x x x x x f x x x R x n = + − + − + + − + ( ) ( ) 1 1 0 ( ) ( ) ( ) (4) 1 ! n n n f R x x x n + + = − + 其中 (3) 是介于 与 之间的某个值 0 x x

在泰勒公式(3)中,如果取。=0,泰勒公式变成带 有拉格朗日型余项的麦克劳林(Maclaurin)公式 f0+09r+0r 21 (n+1)月 (5在0与x之间) 例1写出函数f(x)=e的带有拉格朗日余项的n 阶麦克劳林公式。 e=1+x+ es +.·+一子、《 21 n! (n+1)! (5在0与x之间)
在泰勒公式(3)中,如果取 x0 = 0 ,泰勒公式变成带 ( ) ( 1) 2 ( 1) (0) (0) ( ) ( ) (0) (0) 2! ! ( 1)! n n n n f f f f x f f x x x x n n + + = + + + + + + 有拉格朗日型余项的麦克劳林(Maclaurin)公式 ( 在 0 与 x 之间) ( ) ex 例1 写出函数 f x = 的带有拉格朗日余项的n 阶麦克劳林公式。 2 e 1 e 1 2! ! ( 1)! n x n x x x x n n + = + + + + + + ( 在 0 与 x 之间)
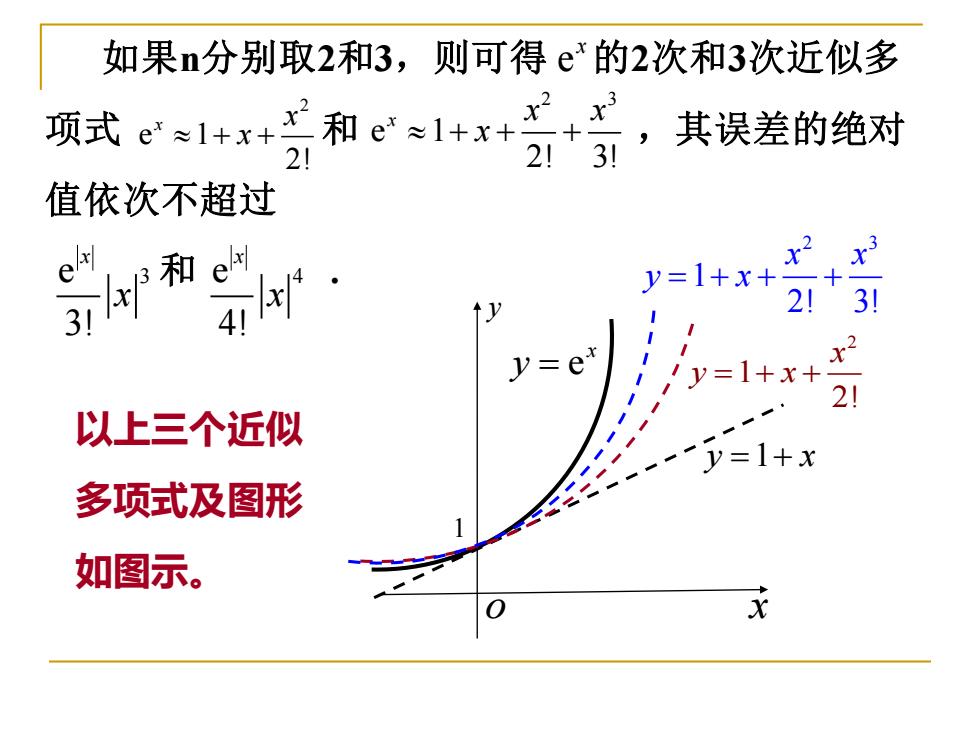
如果n分别取2和3,则可得e的2次和3次近似多 项式。?兰和e1r+于号,其误差的绝对 21 值依次不超过 ew和e 3 y=1+x+ 21 3 v=e y=1 21 以上三个近似 y=1+x 多项式及图形 如图示
如果n分别取2和3,则可得 的2次和3次近似多 项式 和 ,其误差的绝对 值依次不超过 和 . 1 e x y = o x y y x = +1 2 1 2! x y x = + + 2 3 1 2! 3! x x y x = + + + e x 2 e 1 2! x x + +x 2 3 e 1 2! 3! x x x + + + x e 3 3! x x e 4 4! x x 以上三个近似 多项式及图形 如图示

例2写出函数f(x)=six的带有拉格朗日余项的 n阶麦克劳林公式。 sinx=x- x3 (2m-1)川 +R2m(x) in0s+2m1) R2m(x)= 2m+1 0<0<1 (2m+1)川 类似可得: Cosx=1(1)m (2m)! Rn-cos[r+(m+)z] 2m+2 0<0<1 (2m+2)川
例2 写出函数 f x x ( ) sin = 的带有拉格朗日余项的 n阶麦克劳林公式。 ( ) ( ) ( ) ( ) 3 5 2 1 1 2 2 1 2 sin 1 ( ) 3! 5! 2 1 ! sin 2 1 2 ( ) 0 1 2 1 ! m m m m m x x x x x R x m x m R x x m − − + = − + − + − + − + + = + 类似可得: 2 4 2 1 2 1 cos 1 ( 1) ( ) 2! 4! (2 )! m m m x x x x R x m − = − + − + − + + ( ) ( ) 2 2 2 1 cos 1 ( ) 0 1 2 2 ! m m x m R x x m + + + + = +

泰勒多项式逼近 sinx sinx=x-2+5x-责x+岁2++x2m1 y=x-+ 57 3 4 3 y=x- 31十c 6 4
4 2 2 4 6 4 2 0 2 4 6 1 1 1 1 1 3 5 7 9 2 1 ( 1) 3! 5! 7! 9! (2 1)! sin m m m x x x x x x x − − − − = − + − + + + 3! 3 x y = x − 3! 5! 3 5 x x y = x − + 3! 5! 7! 3 5 7 x x x y = x − + − y = x 泰勒多项式逼近 sin x
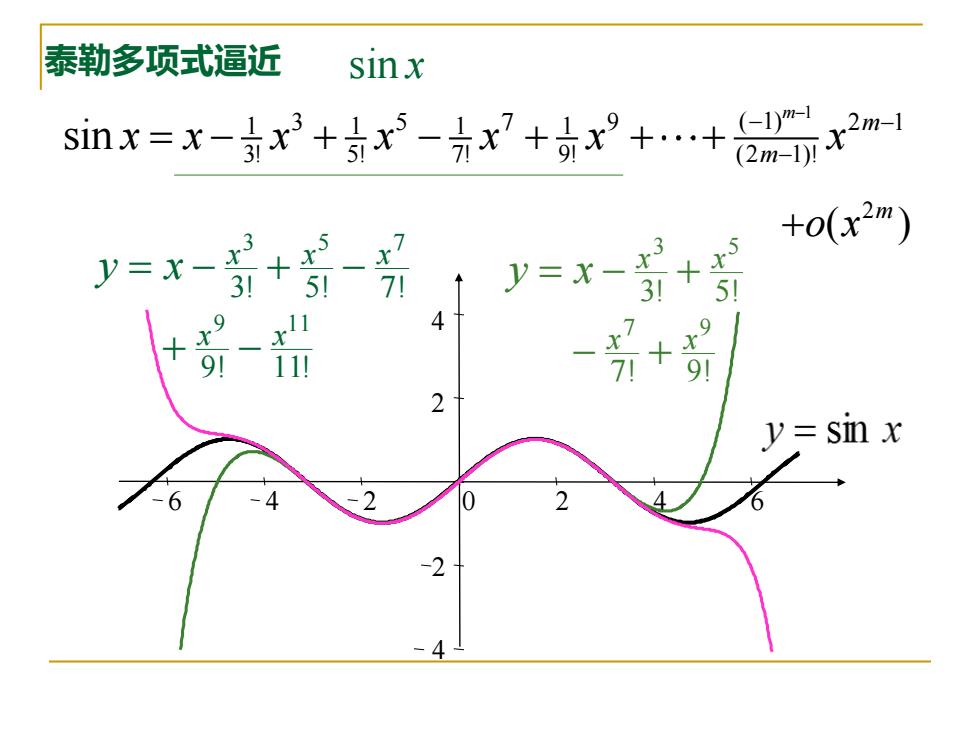
泰勒多项式逼近 sinx simx=x-2+5x-方x+++台x2 +o(x2m) y=x-3 71 5 4 911 91 y=sin x 6
1 1 1 1 1 3 5 7 9 2 1 ( 1) 3! 5! 7! 9! (2 1)! sin m m m x x x x x x x − − − − = − + − + + + 2 ( ) m +o x sin x 4 2 2 4 6 4 2 0 2 4 6 7! 9! 3! 5! 7 9 3 5 x x x x y x − + = − + 9! 11! 3! 5! 7! 9 11 3 5 7 x x x x x y x + − = − + − 泰勒多项式逼近

12 ln(1+x)=x- X1 +1x-+ 2 (+R) n (-1)” R(x)= (n+ (0<0<1) 1+xy=1+ax+aa-》x+. 2! +@(@-1)(@-n+Dx"+R(x) n! B()-a-1)(a(0x00) (n+1)川
1 1 1 ( 1) 2 3 ln(1 ) ( ) 2 3 n n n x x x x x R x n − − + = − + − + + 1 1 ( 1) ( ) (0 1) ( 1)(1 ) n n n n R x x n x + + − = + + 2 ( 1) (1 ) 1 2! ( 1) ( 1) ( ), ! n n x x x n x R x n − + = + + + − − + + + 1 1 ( 1) ( 1)( ) ( ) (1 ) (0 1). ( 1)! n n n n n R x x x n − − + − − − + = + +