华南农业大学：《高等数学》课程PPT教学课件（经济数学B下册）经济数学第20次授课提纲

上次课内容复习 两类区域： X型区域 Y型区域 D={(x,y)p,(x)≤y D={xy),(y)≤x ≤p,(x),a≤x≤b} ≤w,(y),c≤y≤d} ↑y ↑y d d y=0(x) x=必(y) D X= D '2(y) y=o(x) C o a b 0

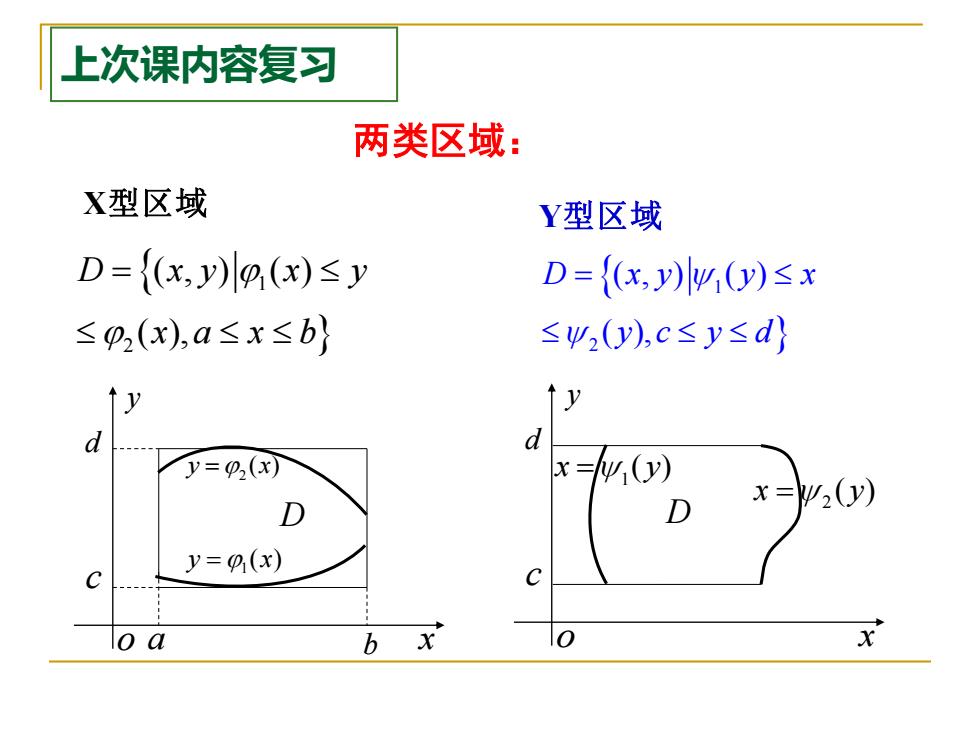
上次课内容复习 两类区域： o x y a b c d 2 y x = ( ) 1 y x = ( )D o x y c d D 1 x y = ( ) 2 x y = ( )   1 2 ( , ) ( ) ( ), D x y x y x a x b   =     X型区域   1 2 ( , ) ( ) ( ), D x y y x y c y d   =     Y型区域

在直角坐标系下二重积分计算的几何解释： z=f(x,y) 1》 y=p(x) y0(x) a b x

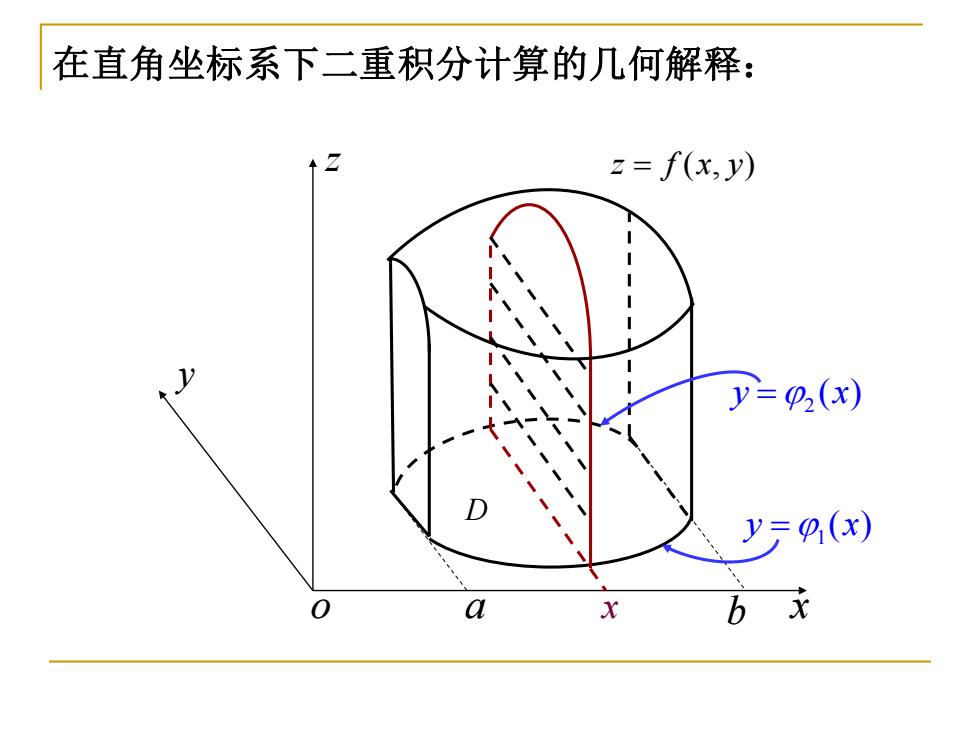
在直角坐标系下二重积分计算的几何解释： o x y z D a b z f x y = ( , ) x 1 y x = ( ) 2 y x = ( )

若f(x,y)在如右图所示的X y 型区域D上连续，其中I(x),(x) y=e(x) D 在[a,b]上连续，则 y=0(x) C ∬f(.yda=-ydy o a b x 若f(x,y)在如右图所示的y 型区域D上连续，其中必y),2y) x=(y) D x=2(y) 在[c,d]上连续，则 ∬fx,do=dfx,k

o x y a b c d 2 y x = ( ) 1 y x = ( )D 若 在如右图所示的 型区域 上连续,其中 在 上连续,则 f x y ( , ) X D 1 2   ( ), ( ) x x [ , ] a b 2 1 ( ) ( ) ( , ) ( , ) b x a x D f x y d dx f x y dy    =    o x y c d D 1 x y = ( ) 2 x y = ( ) 若 在如右图所示的 型区域 上连续,其中 在 上连续,则 f x y ( , ) Y D 1 2   ( ), ( ) y y [ , ] c d 2 1 ( ) ( ) ( , ) ( , ) d y c y D f x y d dy f x y dx    =   

例4计算ed 7其中D是由y=x,y=0及 x=1所围成的区域。 例5计算二次积分 1-h+小 例6计算小川y2-xdo,其中 D={(x,y)川0≤x≤1,0≤y≤1}

例4 计算 其中D 是由 及 所围成的区域。 2 x D e d −  y x y = = , 0 x =1 例5 计算二次积分     − − − = + 1 2 2 2 1 e 0 e e e e e d ln 1 d d ln 1 I d x x x y x y y  − D | y x | d 2 D = {( x, y) | 0  x  1, 0  y  1} 例6 计算 ,其中

例7交换下列积分顺序 1=df0,y+22aFfawy 0≤ysx2 0≤x≤2 x2+y2=8 .J0≤y≤V8-x2 D21 2 2≤x≤22 I-Jf(x.y)dxdy [V8-xi f(x,y)dx 2 2√2

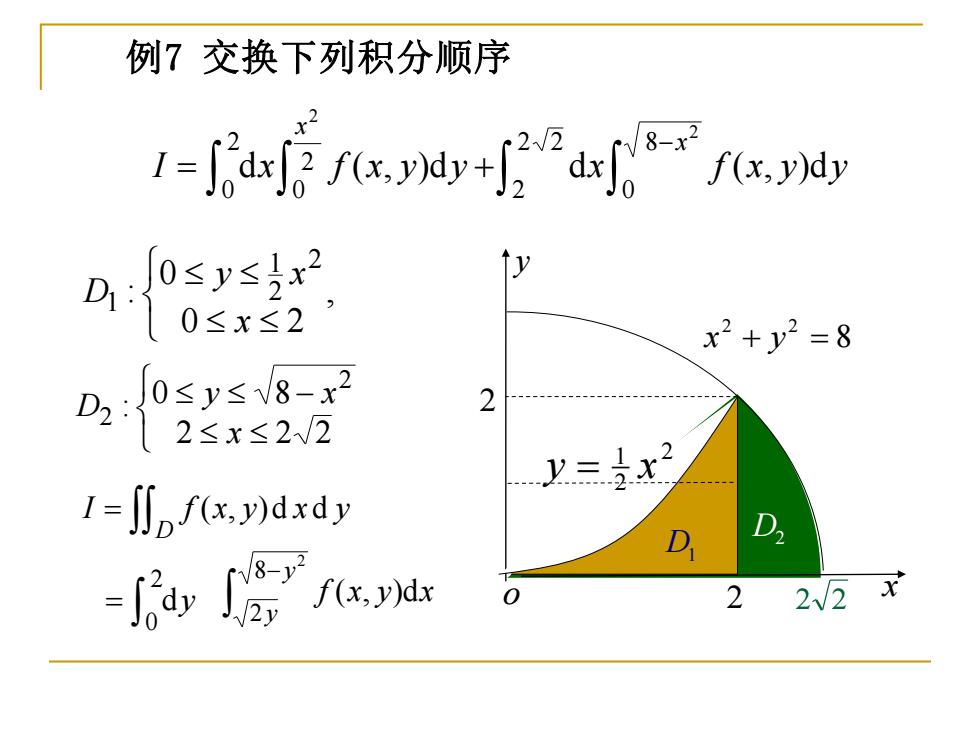
例7 交换下列积分顺序     − = + 2 2 8 0 2 2 2 2 0 2 0 d ( , )d d ( , )d x x I x f x y y x f x y y 8 2 2 x + y = D2 2 2 y o x 2 D1 2 2 1 y = x 2 , 0 2 0 : 2 2 1 1        x y x D        − 2 2 2 0 8 : 2 2 x y x D  = D I f (x, y)d xd y  − 2 8 2 ( , )d y y f x y x  = 2 0 dy

在直角坐标系下二重积分计算方法小结： 画出积分区域的图形 求出边界曲线的交点 (1)计算步骤 确定二次积分次序 进行二次（累次)积分 (2)确定积分次序的依据 积分区域简单 被积函数易积

在直角坐标系下二重积分计算方法小结： （1）计算步骤  画出积分区域的图形 求出边界曲线的交点 确定二次积分次序 进行二次（累次）积分 （2）确定积分次序的依据 积分区域简单 被积函数易积

二、利用极坐标计算二重积分 有些二重积分，其积分区域D是圆域，圆环域或它们 的一部分，D的边界曲线用极坐标表示比较方便，并且 被积函数用极坐标变量p、θ表示比较简单，我们可考 虑用极坐标来计算二重积分 ∬fcx,do 极坐标系： P=常数，表示以极点为中心的一族同心圆。 日=常数，表示从极点出发的一族射线

二、利用极坐标计算二重积分 有些二重积分,其积分区域 是圆域,圆环域或它们 的一部分, 的边界曲线用极坐标表示比较方便,并且 被积函数用极坐标变量 、 表示比较简单,我们可考 虑用极坐标来计算二重积分 D D    D f (x, y)d 极坐标系：  = 常数，表示以极点为中心的一族同心圆。  = 常数，表示从极点出发的一族射线

在极坐标系下，用同心圆P=常数 及射线日=常数，分划区域D为 Q=0g+△0 △ok(k=1,2,.,n) 0=0k 则除包含边界点的小区域外小区 △O为 域的面积 Aok=(P+△P)2·△0-Pg2.A0 =[Pk+(Pk+△Pk]△Pk·A0 P△ =P△Pk·△0 △6 △P △o内取点(p,0),对应有 5=Pr coser,ng=Pr sine

则除包含边界点的小区域外,小区 域的面积 (k 1,2, ,n)  k =  cos , sin k k k k k k       = =  k 内取点 ( , ),  k k 对应有 及射线  =常数, 分划区域 D为 x y o  = k  = k +  k k   =  k 在极坐标系下, 用同心圆  =常数 =      k k k 1 2 2 ( ) = +      k k k  k 1 2 −  2   k k k k  k   k k 

lim ∑f5k,7)△ok 2→ k=1 =lm2f(Aeos8,Asna)p4p,A0 即 f(x)do-f(pcos0,psin0pdpdo pd0

0 1 lim ( cos , sin ) n k k k k k k k k f         → = =    D 即 f (x, y)d ( cos , sin )   d d D = f      d  d  d d

二重积分在极坐标系下化为二次积分的方法： (1)若原点OD,且xy平面上的射线0=常数，与D 的边界至多交于两点，则D必可以表为： P(0)≤p≤p2(0),a≤0≤B, P=P2(0) p=P(0) D dddodp

二重积分在极坐标系下化为二次积分的方法： 1 2         ( ) ( ), ,       D 1    = ( ) 2    = ( ) 2 1 ( ) ( ) ( , ) ( cos , sin ) D f x y dxdy d f d       =           （1）若原点 ，且 平面上的射线 常数，与 的边界至多交于两点，则 必可以表为： O D xy  = D D