
无穷级数习题课 数项级数的审敛方法总结: 包括:正项级数的审敛方法; 交错级数的审敛方法; 一般项级数的审敛方法
无穷级数习题课 数项级数的审敛方法总结: 包括:正项级数的审敛方法; 交错级数的审敛方法; 一般项级数的审敛方法
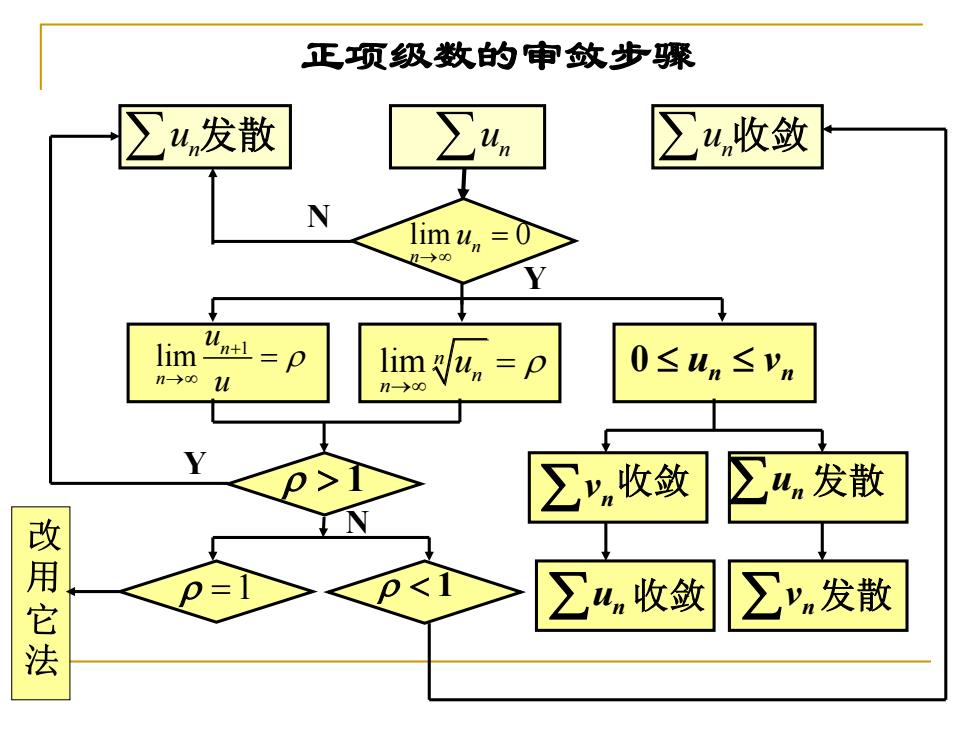
正项级数的审敛步骤 ∑4,发散 ∑4 ∑4,收敛 lim u,=0 Y lim n→00 0≤un≤yn u limu,=p ∑y收敛 ∑4n发散 改用它法 ∑un收敛 ∑yn发散
正项级数的审敛步骤 n u n u 发散 n u 收敛 lim 0 n n u → = N 1 lim n n u u + → = lim n n n u → = n n 0 u v 1 收敛 发散 收敛 n v un un n v 发散 1 Y =1 N Y
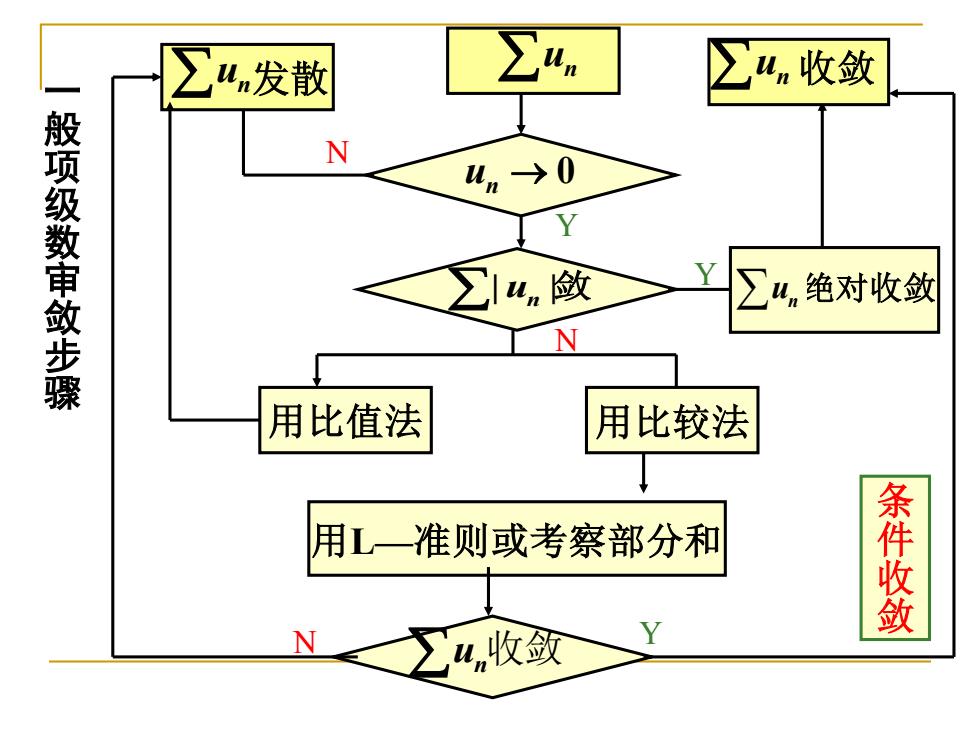
4n发散 ∑4n ∑4收敛 N 般项级数审敛步骤 4n→0 ∑14n做 ∑4,绝对收敛 N 用比值法 用比较法 用L一准则或考察部分和 条件收敛 un收敛
u n → 0 u n N u n 发散 Y | u n |敛 Y u n 绝对收敛 u n 收敛 N 用比值法 用比较法 用L—准则或考察部分和 N u n收敛 Y 条件收敛 一般项级数审敛步骤

例1判断级数 是否收敛?如果收敛, n=1 n -Inn 是条件收敛还是绝对收敛? 解 1>1 >一 n-Inn 而 发散, (-1)” 1 n=l n -Inn un-t 发散, 即原级数非绝对收敛, ,二是交级数,由来布和尼茨定理 Inn Inx ·lim n→+o∞ =lim =lim二=0, x-→+0X x→+o0X
解 , 1 ln 1 n n n − , 1 1 而 发散 n= n , ln 1 ln ( 1) 1 1 发散 = = − = − − n n n n n n n 即原级数非绝对收敛. , ln ( 1) 1 是交错级数 = − − n n n n 由莱布尼茨定理: x x n n n x ln lim ln lim →+ →+ = 0, 1 = lim = x→+ x 例1 是条件收敛还是绝对收敛? 判断级数 是否收敛?如果收敛, = − 1 ( 1) n n n −lnn

1 1 lim- lim- n-=0, n>+oon-nn n→+oo Inn n f(x)=x-Inx (x>0), f=1-1>0(x>I,在L,o)上单增, 即 单减,故1一 x-Inx 当n>1时单减, n-Inn .儿n= n-Inn (n+1)-ln(n+1) =L+1(n>1), 所以此交错级数收敛,故原级数是条件收敛
0, ln 1 1 lim ln 1 lim = − = − →+ →+ n n n n n n n f (x) = x − ln x (x 0), 0 ( 1), 1 ( ) = 1− x x f x 在 (1,+) 上单增, , ln 1 即 单减 x − x 1 , ln 1 故 当 时单减 − n n n ( 1), ( 1) ln( 1) 1 ln 1 = 1 + − + − = u + n n n n n u n n 所以此交错级数收敛,故原级数是条件收敛.

00 例2设正数数列 {an}单调减少,级数∑(-1)-a 00 n= 发散考察 1)”的敛散性 n=1 证 记un=(1+n 由{an}单调减少an>0 故由单调有界原理知iman=A存在且A≥0 n->oo 若A=0由Leibniz审敛法得交错级数 ∑(-1)n收敛,与题设矛盾→A>0 →lim4n=lim,1=.1 n=] <1 n-→1+an1+A 由根值法知 ”收敛
设正数数列 an 单调减少,级数 = − − 1 1 ( 1) n n n a 发散 考察 n n an ) 1 1 ( 1 = + 的敛散性 证 记 n n n a u ) 1 1 ( + = 由 n a 单调减少 0 n a 故由单调有界原理知 an A n = → lim 存在 且 A 0 若 A = 0 由Leibniz审敛法得 交错级数 = − − 1 1 ( 1) n n n a 收敛, 与题设矛盾 A 0 n n n n n a u + = → → 1 1 lim lim 1 1 1 + = A 由根值法知 收敛。 例2 n n an ) 1 1 ( 1 = +

00 例3 讨论 a 的敛散性(p>0,常数) n=1 解对级数 =imna4P1aHa lim n" a1 → 收敛 绝对收敛 0 |a>1 → 发散 n 发散 n=1 |a=1分情况说明
讨论 n=1 p n n a 的敛散性 ( p 0,a常数) 解 对级数 n=1 p n n a ) | | | | 1 lim lim( 1 a a n n u u p n n n n = + = → + → | a | 1 = n 1 p n n a 收敛 = n 1 p n n a 绝对收敛 | a | 1 = n 1 p n n a 发散 = n 1 p n n a 发散 | a |= 1 分情况说明 例3

1 a=1 级数成为 p>1 收敛 p≤1 发散 M=-1 级数成为 白 卫>1绝对收敛 p≤1 条件收敛
a = 1 级数成为 =1 1 n p n p 1 收敛 p 1 发散 a = −1 级数成为 = − 1 ( 1) n p n n p 1 绝对收敛 p 1 条件收敛

课堂练习: 判别下列级数的敛散性: 21 ncos 2n n (2) 2h2 (3) n=1 n=1 1 2 0 00 (4) (a>0,s>0) n=1n 提示:(1):1imn=1,./g>0,3N,当n>N时,有 n>∞ 1 1-8<Wn<1+8=c nn n(1+&) 因调和级数发散,据比较判别法,原级数发散
课堂练习: 判别下列级数的敛散性: 提示: (1) lim =1, → n n n 1− 1+ n n 因调和级数发散, 据比较判别法, 原级数发散 . 0 , N

(n!)2 00 (2) 利用比值判别法,可知原级数发散 2n2 00 n 用比值法,可判断级数 收敛, (3) ∑ 3 n=1 2 再由比较法可知原级数收敛 00 1 (4) 、10 n= 因n充分大时】0,s>0):用l比值判别法可知: a1时发散, s>1时收敛; a=1时,与p级数比较可知 s≤1时发散
利用比值判别法, 可知原级数发散. 用比值法, 可判断级数 因 n 充分大时 , ln 1 1 10 n n ∴原级数发散 . : 2 cos (3) 1 3 2 n= n n n (5) ( 0, 0): 1 = a s n a n s n 用比值判别法可知: 时收敛 ; 时, 与 p 级数比较可知 s 1 时收敛; 时发散. 再由比较法可知原级数收敛 . s 1 a 1 a 1 时发散. a =1 发散, 收敛