
上次课内容复习 ·空间直角坐标系 空间两点的距离公式 ■向量的概念 ·向量的加法和数乘
上次课内容复习 ◼ 空间直角坐标系 ◼ 空间两点的距离公式 ◼ 向量的概念 ◼ 向量的加法和数乘

三、向量的坐标 为了方便后续内容的讨论,我们引进向量的坐标, 即用一组有序的数组来表示向量,从而可以将向量 的运算转化为代数运算, 在空间直角坐标系中引入单位 向量i、广、k,令其方向分别与 x轴、轴、轴的正方向相同, 并称它们为这一坐标系的基本 单位向量
三、向量的坐标 ◼ 为了方便后续内容的讨论,我们引进向量的坐标, 即用一组有序的数组来表示向量,从而可以将向量 的运算转化为代数运算. ◼ 在空间直角坐标系中引入单位 向量i、j、k,令其方向分别与 x轴、y轴、z轴的正方向相同, 并称它们为这一坐标系的基本 单位向量. o x y z i j k
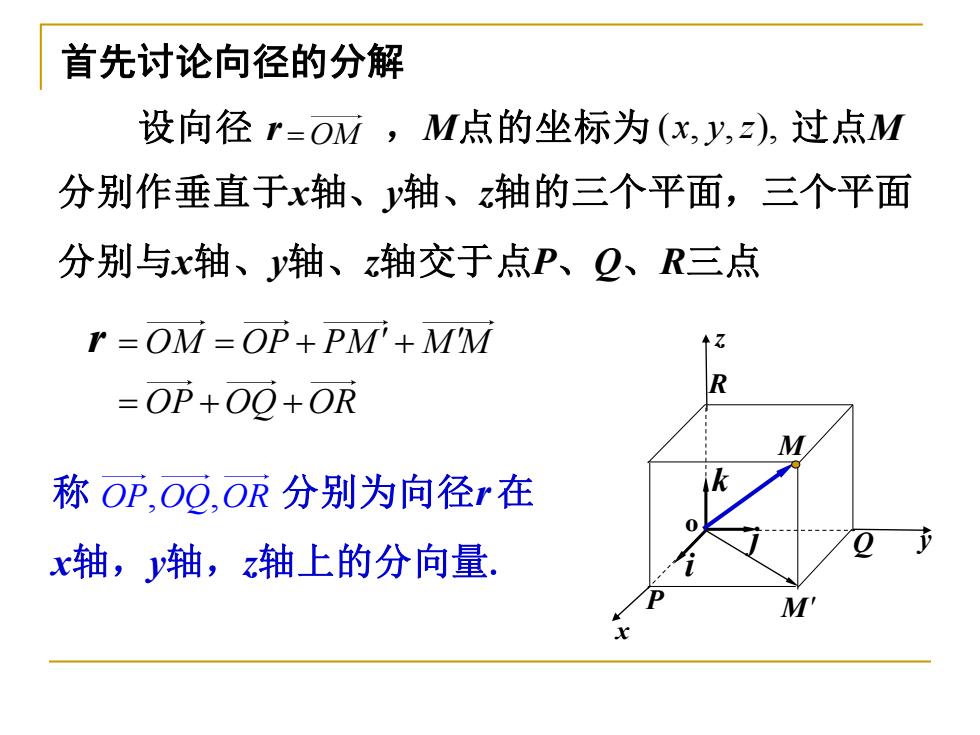
首先讨论向径的分解 设向径r=OM,M点的坐标为(x,y,z),过点M 分别作垂直于x轴、y轴、z轴的三个平面,三个平面 分别与x轴、y轴、z轴交于点P、Q、R三点 r =OM-OP+PM'+M'M ↑Z =OP+00+OR R M 称OP,OO,OR分别为向径r在 x轴,y轴,z轴上的分向量, M
首先讨论向径的分解 r = = + + = + + OM OP PM M M OP OQ OR r = OM ,M点的坐标为 ( , , ), x y z 过点M 分别作垂直于x轴、y轴、z轴的三个平面,三个平面 分别与x轴、y轴、z轴交于点P、Q、R三点 设向径 称 分别为向径r 在 x轴,y轴,z轴上的分向量. OP OQ OR , , x y z o i j k M P R Q M
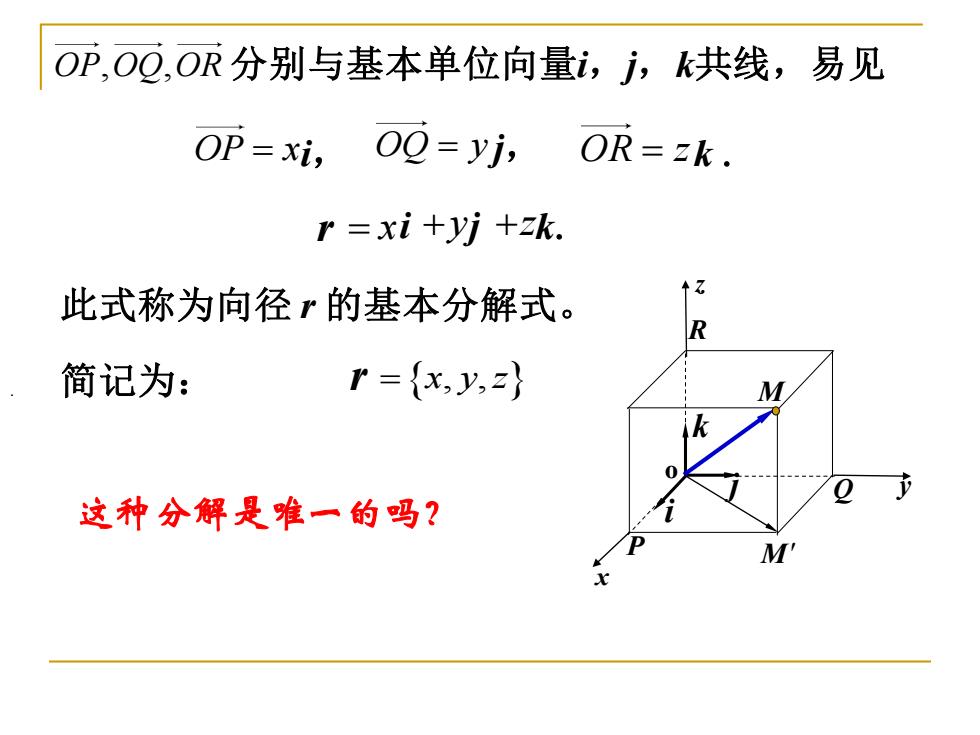
OP,OO,OR分别与基本单位向量i,j,k共线,易见 OP=xi,OQ=yj,OR=zk. r =xi+yi +zk. 此式称为向径r的基本分解式。 R 简记为: r={x,y,2} 0 这种分解是唯一的吗? M
OP OQ OR , , 分别与基本单位向量i,j,k共线,易见 r = x i +y j +z k. OP x = i, OQ y = j, OR z = k . . r =x y z , , 此式称为向径 r 的基本分解式。 简记为: 这种分解是唯一的吗? x y z o i j k M P R Q M

由向量的运算规则容易得到任意向量的这种分 解,其分解过程如下:设a=MM,为任意向量, 起点M的坐标是(x,),终点M2的坐标是(x,2), 则向径 r=OM1=xi+j+名k =OM2 x2i+yj+52k a=MM,=OM,-OM=n-n =(x2i+y2j+22k)-(xi+yj+2k) =(x2-x)i+(0y2-y)j+(32-2)k
由向量的运算规则容易得到任意向量的这种分 解,其分解过程如下: x z o y 1 r 2 r M1 M2 a 则向径 1 r = = OM x 1 1 i 1 + y j 1 +z 2 r = = OM x 2 2 i 2 +y j 2 +z k k 设 a = M M1 2 为任意向量, M1 的坐标是 1 1 1 ( , , ) x y z ,终点 M2 的坐标是 2 2 2 起点 ( , , ) x y z , a = = − = M M OM OM 1 2 2 1 r r 2 2 − = 2 (x i 2 +y j 2 +z k)-( 1 x i + 1 y 1 j +z k) j 2 1 = − ( ) x x i 2 1 + − ( ) y y 2 1 + − ( ) z z k

令a=(x2-x),a,=(y2-y),a=(2-1) 则有 a=aitayjta.k 上式称为向量α的基本单位向量分解式。 axi,aj,ak分别称为向量a在x轴,y轴,z轴上的 分向量; a,ay,a,分别为向量a在x轴、y轴、z轴上坐标。 起点为M1(x,)而终点为M,(x2,2,二2)的向量为: MM,={x2-x,当-,2-1};oM={xy,z}
令 2 1 2 1 2 1 ( ), ( ), ( ) x y z a x x a y y a z z = − = − = − M M x x y y z z 1 2 2 1 2 1 2 1 = − − − , , ; 则有 上式称为向量 a 的基本单位向量分解式。 x = a i y +a j z a +a k 分别称为向量a在x轴,y轴,z轴上的 分向量; a a a x y z i, j, k x a ay , z , a 分别为向量a在x轴、y轴、z轴上坐标。 M1 1 1 1 ( , , ) x y z 而终点为 M2 2 2 2 起点为 ( , , ) x y z 的向量为: oM x y z = , , .

两向量相等,当且仅当其坐标相等. 向量a={a,a,a}的模的坐标表示式为: a-yata+a 若向量a≠0且a与平行,则b= bb,b-3=Aas,av,a. 这就相当于向量与b对应的坐标成比例: bs by b. ax ay a2
两向量相等,当且仅当其坐标相等. 向量 a = a a a x y z , , 的模的坐标表示式为: a 222 x y z = + + aaa 若向量 a 0 且 a 与 b 平行,则 b = a { , , } { , , } bx by bz = ax ay az 这就相当于向量 a 与 b 对应的坐标成比例: z z y y x x a b a b a b = =

例2己知两点M,(x,二)和M,(x,52,22)以及实数 ≠-b在直线M,M2上求点M,使得 MM=AMM, 四、向量的数量积和方向余弦 1.向量的数量积 定义两个向量的模与和b它们夹角的余弦的 乘积,称作两向量a和b的数量积(或内积),记做 ab,即 ab=4 cose
例2 已知两点 ( , , ) 1 1 1 1 M x y z 和 ( , , ) 2 2 2 2 M x y z 以及实数 −1 ,在直线 M1 M2 上求点 M M M MM 1 2 = ,使得 。 四、向量的数量积和方向余弦 1.向量的数量积 定义 两个向量的模与 a 和 b 它们夹角的余弦的 a b a b a b = cos 乘积,称作两向量a和b的数量积(或内积),记做 ,即

2.数量积的坐标表示式和运算规律 数量积运算的坐标表示式为 a.b=ab +a b,+a.b 即两向量的数量积等于它们对应坐标的乘积之和. 数量积满足下列三条运算规律: 1.交换律mb=b· 2.分配律(a+b)c=ac+bc 3.结合律(2a)b=(ab),元为数量
2.数量积的坐标表示式和运算规律 数量积运算的坐标表示式为 a b = a b a b a b x x y y z z + + 即两向量的数量积等于它们对应坐标的乘积之和. 数量积满足下列三条运算规律: a b b a = 2.分配律 ( ) a b c a c b c + = + 3.结合律 ( ) ( ) a b a b = , 为数量. 1.交换律

3.向量的方向余弦 向量可以用它的模和方向表示,也可以用它的坐标 来表示,为了应用上的方便,需要沟通向量的坐标和 向量的模及方向之间的联系. a, cosa= a+a+a cos B= va +a;+a' a cosy= Ja+a+a cos2 a+cos2 B+cos2y =1
3.向量的方向余弦 x y z o i j k a 向量可以用它的模和方向表示,也可以用它的坐标 来表示,为了应用上的方便,需要沟通向量的坐标和 向量的模及方向之间的联系. 222 222 222 cos cos cos x x y z y x y z z x y z a aaa a aaa a aaa = + + = + + = + + 2 2 2 cos cos cos + + =1