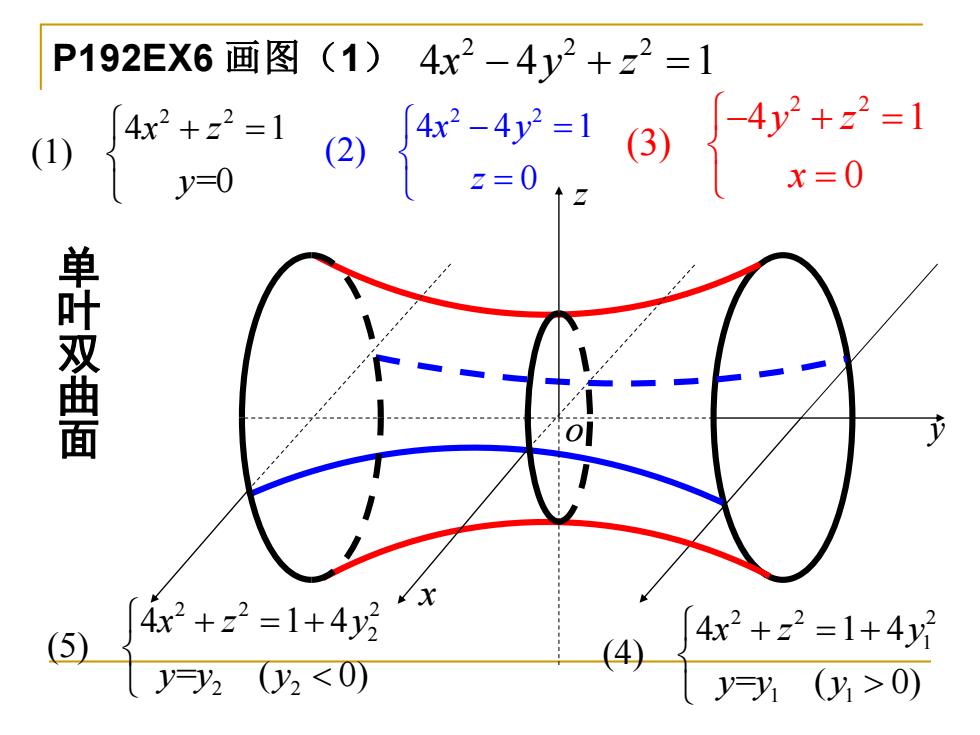
P192EX6画图(1)4x2-4y2+z2=1 (1) y=0 x=0 单叶双曲面 4x2+z2=1+4y (5) (4) 4x2+z2=1+4y7 y2(0y20
P192EX6 画图(1) 2 2 2 4 4 1 x y z − + = x o z y 2 2 4 1 (1) =0 x z y + = 2 2 4 4 1 (2) 0 x y z − = = 2 2 4 1 (3) 0 y z x − + = = 2 2 2 1 1 1 4 1 4 (4) = ( 0) x z y y y y + = + 2 2 2 2 2 2 4 1 4 (5) = ( 0) x z y y y y + = + 单 叶 双 曲 面

P192EX6画图(2) +2=1 916 椭圆抛物面
P192EX6 画图(2) 2 2 1 9 16 x y + + =z 椭 圆 抛 物 面 x o z y
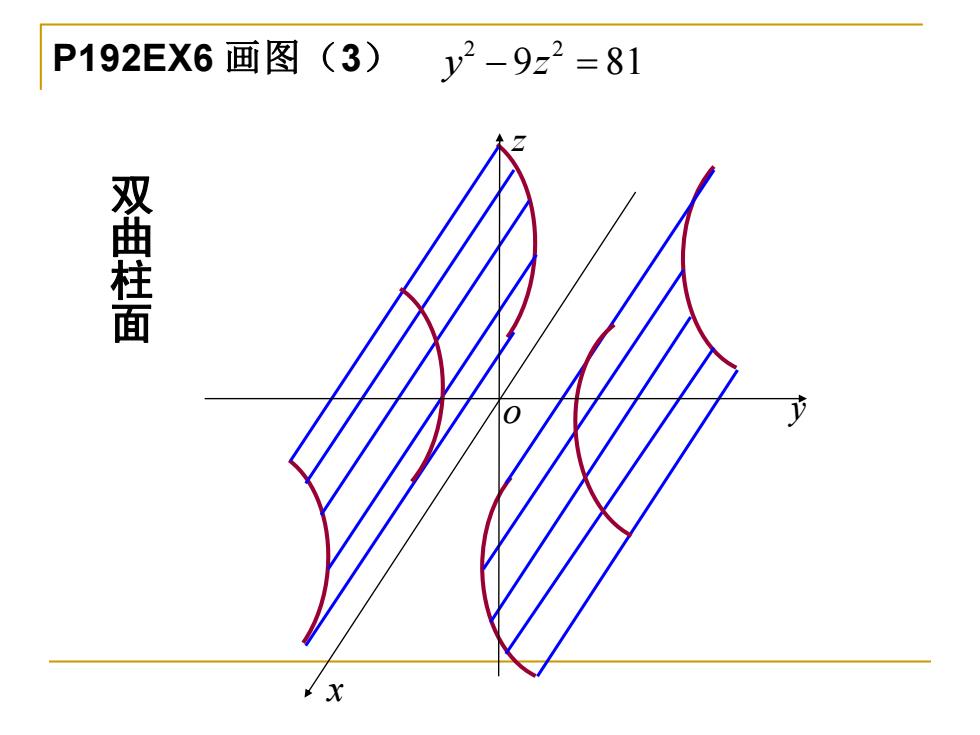
P192EX6画图(3)y2-9z2=81 双曲柱面 0
P192EX6 画图(3) 2 2 y z − = 9 81 x o y z 双 曲 柱 面

P192EX6画图(4)x2y2 +z2=-1 4 双叶双曲面
x o z y P192EX6 画图(4) 2 2 2 1 4 9 x y − + = − z 双 叶 双 曲 面

习题课(多元函数与偏导数部分) 一、多元函数 1.平面点集的有关概念 内点;外点;界点。 聚点;孤立点。 一些重要的平面点集 2.多元函数的定义及其几何意义
习题课(多元函数与偏导数部分) 一、多元函数 1. 平面点集的有关概念 内点;外点;界点。 聚点;孤立点。 一些重要的平面点集 2. 多元函数的定义及其几何意义

3.多元函数的极限 4.多元函数的连续性 二、偏导数 1.一阶偏导数 2.高阶偏导数
3. 多元函数的极限 4. 多元函数的连续性 二、偏导数 1. 一阶偏导数 2. 高阶偏导数

三、教学要求 求解函数的定义域; 会求简单的极限; 会证明简单的极限问题和极限不存在的问题; 理解多元函数的连续性的概念; 熟练掌握偏导数的求法; 掌握界点处偏导数的求法。 理解多元函数在一点处有定义、极限存在、 连续、偏导数存在的内在联系
三、教学要求 求解函数的定义域; 会求简单的极限; 会证明简单的极限问题和极限不存在的问题; 熟练掌握偏导数的求法; 理解多元函数的连续性的概念; 掌握界点处偏导数的求法。 理解多元函数在一点处有定义、极限存在、 连续、偏导数存在的内在联系

例1求极限 1-c0s(x2+y2) lim x,-o,0)(x2+y2)ln(1+x2+y2) 例2求极限 lim sin(x2y) 2+y2 y→0 例3求极限 11 lim (x+y)sin-cos- (x,y)-→(0,0) x y
例1 求极限 2 2 2 2 2 2 ( , ) (0,0) 1 cos( ) lim ( )ln(1 ) x y x y → x y x y − + + + + 例2 求极限 . sin( ) lim 2 2 2 0 0 x y x y y x + → → 例3 求极限 ( , ) (0,0) 1 1 lim ( )sin cos x y x y → x y +

例3求极限 lim sin(x2y) →0 x2+y2 y→0 sin(x y)=lim sin(x2y).x2y 解 lim 9x2+y2 x→0 y-→0 y-→0 x2yx2+y2” lim sin(x"y) sin u 其中 u=x'y x'y =1, x-→0 u-→0 y-→0 x2+y2 2 00, 2 ∴.lim sin(x"y) =0. 0x2+y2 ’→0
例3 求极限 . sin( ) lim 2 2 2 0 0 x y x y y x + → → 解 2 2 2 0 0 sin( ) lim x y x y y x + → → , sin( ) lim 2 2 2 2 2 0 0 x y x y x y x y y x + = → → 其中 x y x y y x 2 2 0 0 sin( ) lim → → u x y 2 = u u u sin lim →0 = 1, 2 2 2 x y x y + x 2 1 0, ⎯x→⎯0→ 0. sin( ) lim 2 2 2 0 0 = + → → x y x y y x

例4试证明函数 f(x,)= x2+y4)7 当(x,y)→(0,0)时,极限不存在。 例5讨论函数 f(x,y)=vx2+y2, 在(0,0)的连续性和偏导数的存在性
例4 试证明函数 3 2 2 4 2 ( , ) ( ) x y f x y x y = + 当 (x, y) → (0,0) 时,极限不存在。 例5 讨论函数 ( , ) , 2 2 f x y = x + y 在(0,0)的连续性和偏导数的存在性