
第一章 第二节数列的极限 (Limits of Sequences) 极限方法是高等数学中的一种基本方法.本节 主要介绍数列极限的概念以及收敛数列的性质, 一、数列极限的定义 二、收敛数列的性质 2009年7月3日星期五 1 目录 上页 下页 、返回
2009年7月3日星期五 1 目录 上页 下页 返回 第二节 数列的极限 (Limits of Sequences) 第一章 极限方法是高等数学中的一种基本方法.本节 主要介绍数列极限的概念以及收敛数列的性质 . 二、收敛数列的性质 一、数列极限的定义

一、数列极限的定义 L.数列(Sequence of number)) 如果按照某一法则,对每个n∈Z,对应着一个确定的 实数Xn,这样无穷多个实数x,2,.,xn,.按次序一个接 一个地排列下去,就构成了一个数列,简记为{x}. 数列中的每一个数叫做数列的项,第项x,称为数列的 一般项或通项,例如数列: 234n+1 n+l (1)123n 通项为 (2)-1,1,-1,1.-1,1,-1,1. 通项为(-1)” 2009年7月3日星期五 2 目录○ 上页 下页 返回
2009年7月3日星期五 2 目录 上页 下页 返回 一、数列极限的定义 1. 数 列(Sequence of number) 如果按照某一法则, 对每个 n Z + ∈ , 对应着一个确定的 实数 n x , 这样无穷多个实数 123 , n xxx x " " 按次序一个接 一个地排列下去, 就构成了一个数列, 简记为 { x n } . 数列中的每一个数叫做数列的 项, 第 n 项 n x 称为数列的 一般项 或通项, 例如数列: (1) 234 1 , , , 123 n n + " " 通项为 n 1 n + ( 2 ) −− −− 1,1, 1,1 1,1, 1,1 " " 通项为( 1) n −

(3)5,V3+3,.,/3+V3+V.+3, 通项为x+1=Vxn+3且x=V3. 事实上, 一方面数列给出了一个以正整数集为定义域的函数, 此函数称为整标函数,即xn=f(n). 另一方面,在几何上数列对应着数轴上一个点列, 可看作依次在数轴上取,X2,.,xn,.的动点. X3X1x2七4xn 2009年7月3日星期五 3 目录 (上页 下页 、返回
2009年7月3日星期五 3 目录 上页 下页 返回 ( 3 ) 3, 3 3, , 3 3 3 , + ++ + " " 通项为 1 3 n n x x + = + 且 1 x = 3 . 事实上, 一方面数列给出了一个以正整数集为定义域的函数, 此函数称为整标函数, 即 ( ) n x = f n . 另一方面, 在几何上数列对应着数轴上一个点列, 可看作依次在数轴上取 1 2 , n xx x " "的动点. x 3 x 1 x 2 x 4 x n
2.数列极限的定义 我们先来观察数列1+-) 当n无限增大时, n 即n→o时的变化趋势 1.75 1.5 1.25 1 0.75 0.5 0.25 8 10 12 图形演示 2009年7月3日星期五 4 目录○ 上页 下页 返回
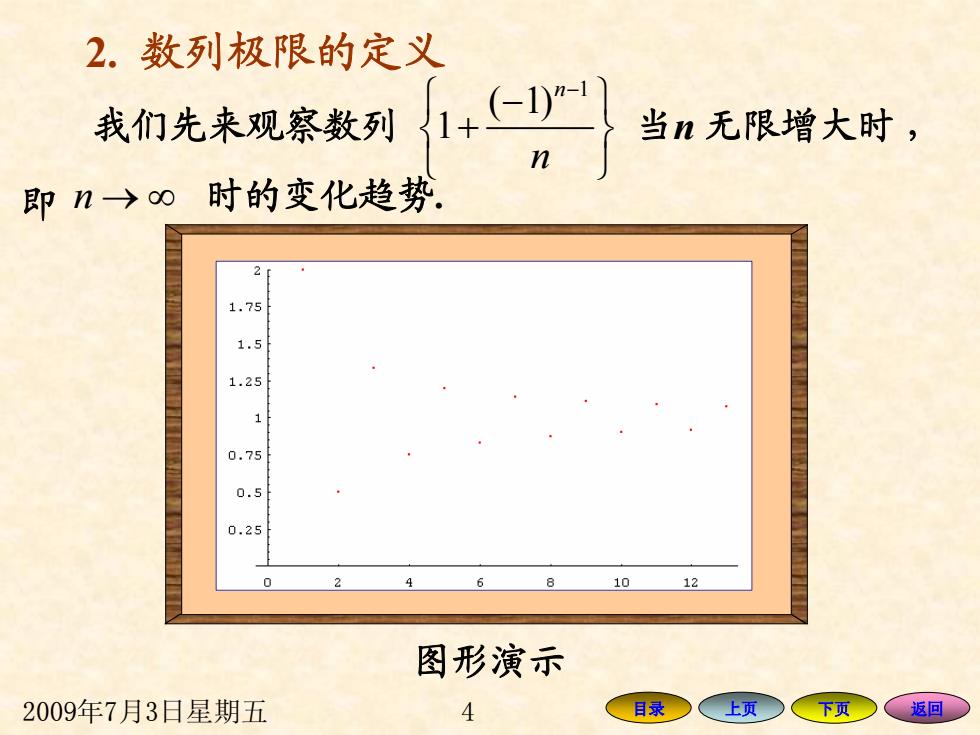
2009年7月3日星期五 4 目录 上页 下页 返回 2. 数列极限的定义 我们先来观察数列 1 ( 1) 1 n n − ⎧ − ⎫ ⎨ + ⎬ ⎩ ⎭ n → ∞ 时的变化趋势 . 当n 无限增大时 , 即 图形演示

通过上面演示实验的观察知: 当n无限增大,一般项x,=1+少 无限接近于常数1. 怎样用精确的数学语言来阐述“当趋于无穷大时, 数列xn无限接近一个确定的常数α”这一变化趋势? 我们知道,两个数a与b之间的接近程度可以用这两个 数之差的绝对值|b-a来度量(|b-a的几何意义表示,点a 与点b之间的距离),b-a越小,a与b就越接近.为此,“数 列x,无限接近一个确定的常数a”,就是|xn-a可以任意小, 也就是说|xn-a可以小于预先给定任意小的正数; “n趋于无穷大”就是要n充分大,大到足以保证|xn-a 可以小于预先给定任意小的正数, 2009年7月3日星期五 5 目录 上页 下页 、返回
2009年7月3日星期五 5 目录 上页 下页 返回 通过上面演示实验的观察知: 当 n 无限增大,一般项 ( 1) 1 n n x n − = + 无限接近于常数 1. 怎样用精确的数学语言来阐述“ 当 n 趋于无穷大时, 数列 n x 无限接近一个确定的常数 a ”这一变化趋势? 我们知道, 两个数 a 与 b 之间的接近程度可以用这两个 数之差的绝对值| | b a − 来度量 (| | b a − 的几何意义表示点 a 与点 b 之间的距离),| | b a − 越小, a 与 b 就越接近. 为此,“数 列 n x 无限接近一个确定的常数 a ” , 就是| | n x − a 可以任意小, 也就是说| | n x a − 可以小于预先给定任意小的正数; “ n 趋于无穷大”就是要 n 充分大, 大到足以保证| | n x a − 可以小于预先给定任意小的正数.

对于数列x,=1+一) n 给定正数 ,只要n>100时,就有1x,-1K 1 10 0 1 给定正数 1000 ,只要n>1000时,就有x,-10000时,税有E,0 10000 一般地, 对于文任意小正纸风刘[目时 就有。-<成立,我们就称数列x,=1+少 (n=1,2,.) 当n趋于无穷大时的极限为1. 2009年7月3日星期五 6 目录 上页 下页 返回
2009年7月3日星期五 6 目录 上页 下页 返回 对于数列 ( 1) 1 n n x n − = + , 给定正数 1 100 , 只要 n >100时, 就有 1 | 1| 100 n x − 1000 时,就有 1 1 1000 n x − 10000 时,就有 1 1 10000 n x − =⎜ ⎟ ⎢ ⎥ ⎝ ⎠ ⎣ ⎦ 时, 就有 1 n x − < ε 成立, 我们就称数列 ( 1) 1 ( 1,2, ) n n x n n − =+ = " 当 n趋于无穷大时的极限为 1.

定义 设有数列{xn}和常数a,如果对任意给定的正数e (无论它多么小),总存在正整数N,使得对于n>N的一切xm, 不等式 lxm-a0,3正整数N,当n>N时,有|xn-aks. n→00 2009年7月3日星期五 目录 上页 下页 返回
2009年7月3日星期五 7 目录 上页 下页 返回 定义 设有数列 { x n } 和常数 a , 如果对任意给定的正数 ε (无论它多么小), 总存在正整数 N , 使得对于n N> 的一切 n x , 不等式 n x a − ∃ ε 0, 正整数 N ,当 n N > 时,有| | n x a − < ε .

limx=a台&>0,3正整数N,当n>W时,有|xn-ak. n-→0 这就是所谓的“£-N”定义 不等式xn-adN时,即从点xw 以后,所有的点x,都落在开区间(a-6,a+8)内,所有的点xn都 落在开区间(a-8,a+)内,而只有有限个点(至多只有N个) 在这区间以外, 28 a-E a+8 X2 X1 XN+1 XN+2 3 2009年7月3日星期五 8 目录 上页 下页 、返回
2009年7月3日星期五 8 目录 上页 下页 返回 这就是所谓的“ ε − N ”定义. lim n n x a →∞ = ⇔ ∀> ∃ ε 0, 正整数 N ,当 n N > 时,有| | n x a − 时, 即从点 N x 以后, 所有的点 n x 都落在开区间(,) a a − ε + ε 内, 所有的点 n x 都 落在开区间(,) a a − + ε ε 内, 而只有有限个点(至多只有 N 个) 在这区间以外. x x 2 x 1 x N + 1 x N + 2 x 3 2 ε a − ε a + ε a

例1已知xn=C(常数),证明数列{xn的极限为C 证:H&>0,对一切自然数n, xn-C=C-C=0N时,有不等式xn-aks成立,但没有必要 去求最小的N. 2009年7月3日星期五 9 目录 上页 下页 返回
2009年7月3日星期五 9 目录 上页 下页 返回 n x C= 证明数列 { x n }的极限为 C. 证: ∀ ε > ,0 例1 已知 对一切自然数 n , n − Cx = − CC = 0 时, 有不等式| | n x a − < ε 成立, 但没有必要 去求最小的 N.

例2证明 lim (-1)” =0 n-→ (n+8)3 运-0-yGis4 n ε∈(0,1),欲使xn-0 n 取N母则当n>N时,就有x,-0k, 故limx=lim (1)” =0 n-→00 n-→(n+8)3 也可由x,-0= (n+8) 说明:N与有关,但不唯一 取N= 不一定取最小的N」 2009年7月3日星期五 10 目录 上页 下页 返回
2009年7月3日星期五 10 目录 上页 下页 返回 3 ( 1) lim 0 ( 8) n n→∞ n − = + 证 : x n 0 =− 3 ( 1) 0 ( 8) n n − − + 3 1 ( 8) n = + 例2 证明 1 n 8 取 1 N , ε ⎡ ⎤ = ⎢ ⎥ ⎣ ⎦ 则当 n > N 时, 就有 x n − < ε ,0 1 . ε 故 3 ( 1) lim lim 0 ( 8) n n n n x →∞ →∞ n − = = + 1 0 , 8 n x n − < + 故也可取 1 N 8 ε ⎡ ⎤ = − ⎢ ⎥ ⎣ ⎦ 也可由 3 1 0 ( 8) n x n − = + N 与 ε 有关, 但不唯一. 不一定取最小的 N . 说明: 取 3 1 N 8 ε ⎡ ⎤ = − ⎢ ⎥ ⎣ ⎦