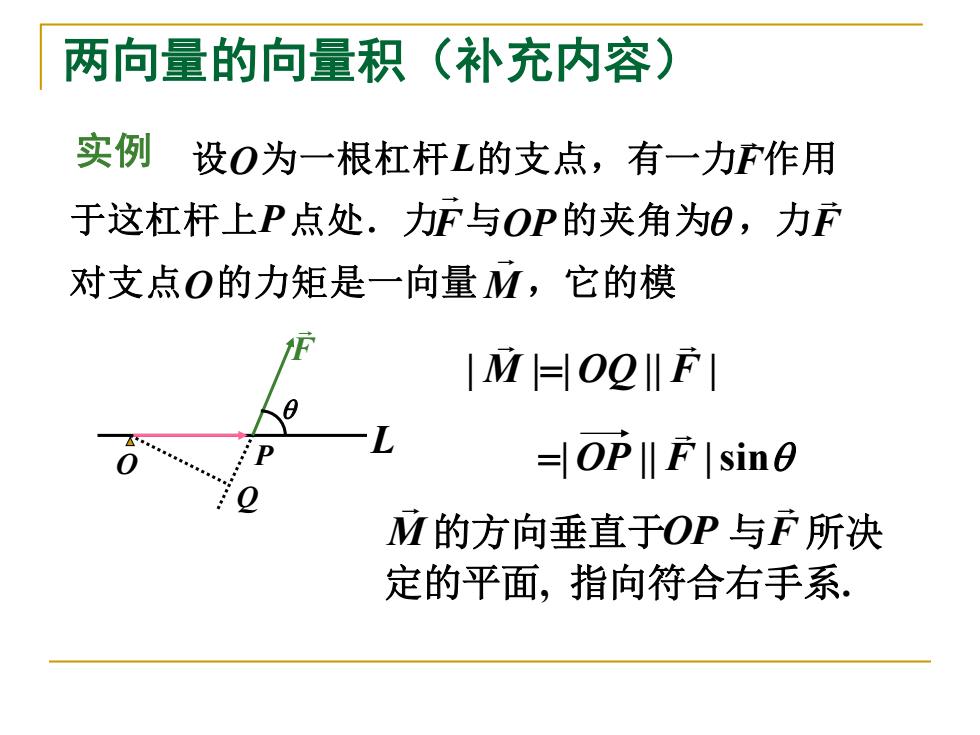
两向量的向量积(补充内容) 实例 设0为一根杠杆L的支点,有一力疗作用 于这杠杆上P点处.力F与OP的夹角为0,力F 对支点O的力矩是一向量M,它的模 |M曰O9‖F1 =OP‖lF|sin0 M的方向垂直于OP与F所决 定的平面,指向符合右手系
| M | | OQ || F | = | OP || F |sin = M 的方向垂直于OP 与F 所决 定的平面, 指向符合右手系. 两向量的向量积(补充内容) L F P Q O 实例 设O为一根杠杆L的支点,有一力F 作用 于这杠杆上P点处.力F 与OP的夹角为 ,力F 对支点O的力矩是一向量 M ,它的模

定义向量a与b的向量积为c=a×b |c=a‖b|sin0(其中o为d与6的夹角) c的方向既垂直于,又垂直于万,指向符合 右手系 向量积也称为“叉积”、“外积 关于向量积的说明: (1d×i=0.(.0=0→sin0=0) (2)aWb←→d×b=0.(a≠0,b≠0)
关于向量积的说明: (1) 0. a a = ( = 0 sin = 0) a b (2) // 0. a b = ( 0, 0) a b 向量积也称为“叉积”、“外积 ”. 向量a 与b 的向量积为 c a b = | c | | a || b |sin = 定义 c 的方向既垂直于a ,又垂直于 b ,指向符合 右手系. (其中为a 与b 的夹角)

证(台):a×b=0,1≠0,1b≠0, ∴.sin0=0,0=0,alWb (←).aWb.0=0或π.∴.sin0=0 |a×b=alb1sin0=0. 向量积符合下列运算规律: (1)axb=-b×a. (2)分配律:(a+b)×c=d×c+b×c. (3)若伪数(2d)×b=d×(2b)=(a×b)
向量积符合下列运算规律: (1) a b b a. = − (2)分配律: (a b) c a c b c. + = + (3)若 为数 ( a) b a ( b) (a b). = = () 0, a b = | a | 0, | b | 0, sin = 0, = 0, () sin = 0 | a b |=| a || b |sin = 0. 证 a b // a b // = 0或

设d=ai+a,j+aE,万=bi+bj+bk axB=(ai+a,j+a,k)x(bi+b,j+b.k) ixi=jxj=kxk=0, .i×j=k,j×k=i,kxi=j, j×i=-k,k×j=-i,i×k=-j. =(a,b:-a,by)i+(a,bx-a b.)j+(a b,-abs)k 向量积的坐标表达式
a a i a j a k, x y z = + + b bx i by j bzk 设 = + + a b = (a i a j a k) x y z + + (b i b j b k) x y z + + i j k, = 0, i i = j j = k k = k i j, j k i , = = j i k, = − i k j. k j i , = − = − a b a b i a b a b j a b a b k y z z y z x x z x y y x = ( − ) + ( − ) + ( − ) 向量积的坐标表达式

向量积还可借助于三阶行列式表示 i ax a×b= x b. by bx b b 由上式可推出 ab2-b42=0 aWb←←→axb=0=→ a b-ba,=0 a b,-bay =0
向量积还可借助于三阶行列式表示 x y z x y z b b b a a a i j k a b = k b b a a j b b a a i b b a a x y x y x z x z y z y z = − + 由上式可推出 a b // 0 a b = aybz − byaz = 0 axbz − bxaz = 0 axby − bxay = 0

←→ bs by b. bx、b、b,不能同时为零,但允许两个为零, 例如, 4=0=2→4=0,0,=0 00b. 补充 c=i×b |d×b|表示以i和b为邻边 b 的平行四边形的面积
z z y y x x b a b a b a = = bx、by、bz不能同时为零,但允许两个为零, 例如, z x y z b a a a = = 0 0 ax = 0, ay = 0 补充 | a b | 表示以a 和b 为邻边 的平行四边形的面积. a b c a b =

例求与d=3i-2j+4k,b=i+i-2k都垂直 的单位向量. 解 c=axb=a ay a =3-2 4=10j+5k, byby b. 11 -2 .|c=W102+52=5V5, 见教材P179例2 -±后=+
例 求与a i j k = 3 − 2 + 4 ,b i j k = + − 2 都垂直 的单位向量. 解 x y z x y z b b b a a a i j k c a b = = 1 1 2 3 2 4 − = − i j k 10 j 5k, = + | | 10 5 5 5, 2 2 c = + = | | 0 c c c = . 5 1 5 2 = j + k 见教材P179例2

习题课 一、主要内容 (一)向量代数 (二)平面及其方程
习 题 课 一、主要内容 (一)向量代数 (二)平面及其方程

1、向量的概念 向量的模、单位向量、零向量、 自由向量、相等向量、负向量、 平行向量、向径. 2、向量的线性运算 加、减、数乘
1、向量的概念 向量的模、单位向量、零向量、 自由向量、 相等向量、 负向量、 平行向量、 向径. 2、向量的线性运算 加、减、数乘

3、向量的表示法 向量的分解式: 在三个坐标轴上的分向量: 向量的坐标表示式: 向量的坐标: 模、方向余弦的坐标表示式 4、数量积、向量积 各种积的坐标表达式 两向量平行、垂直的条件
向量的坐标表示式: 向量的坐标: 模、方向余弦的坐标表示式 4、数量积、向量积 各种积的坐标表达式 两向量平行、垂直的条件 3、向量的表示法 向量的分解式: 在三个坐标轴上的分向量: