
第十章 微分方程与差分方程 上次课内容复习: 1、微分方程的基本概念; 2、微分方程的通解与特解; 3、可分离变量的微分方程及其求解方法。 本次课后作业:EX10-23,4,5
第十章 微分方程与差分方程 上次课内容复习: 1、微分方程的基本概念; 2、微分方程的通解与特解; 3、可分离变量的微分方程及其求解方法。 本次课后作业:EX 10-2 3, 4, 5

§10.2可分离变量的微分方程与齐次方程 二、齐次方程 在一阶微分方程中,可化为形如 dx 的微分方程,称为一阶齐次微分方程,简称齐次方 程 在齐次方程(3)中令 u=上得y= u 两边求导得 dy=u+x dx dx
§10.2 可分离变量的微分方程与齐次方程 二、齐次方程 在一阶微分方程中,可化为形如 dy y dx x = 的微分方程,称为一阶齐次微分方程,简称齐次方 程. x y u = 得 y = ux 两边求导得 d d d d y u u x x x = + 在齐次方程(3)中令

将其代入方程,得 du u+x- dx -o(u) 这是可分离变量的方程,分离变量并两边积分,得 。 求出积分后,再用上代替u X 便得所给齐次方程的通解
将其代入方程,得 d ( ) d u u x u x + = 这是可分离变量的方程,分离变量并两边积分,得 = − x x u u u d ( ) d x y 求出积分后,再用 代替 u 便得所给齐次方程的通解.

例如方程 x2d-(x3+y2y=0 可以变形为 y X
例如方程 d ( )d 0 2 3 3 x y x − x + y y = 可以变形为 2 3 3 3 d ( , ) d 1 y y x y x f x y x x y y x = = = + +

例1求方程 dx =xy-y2 满足初始条件儿=1的特解. 例2求方程 =y+tan 的通解。 dx
例1 求方程 2 2 d d x y y x y x = − 满足初始条件 1 1 = x= y 的特解. 例2 求方程 x y x y dx dy = + tan 的通解

例3求方程 (x3-y3)dy-x2ydx=0 的通解. 例4求方程 2y2-2y'=x dx dx 的通解
例3 求方程 ( )d d 0 3 3 2 x − y y − x y x = 的通解. 例4 求方程 dx dy y x dx dy x y 2 3 3 2 − 2 = 的通解
例5抛物线的光学性质 实例:车灯的反射镜面 旋转抛物面 解 如图设旋转轴ox轴 光源在(0,0),L:y=y(x) 设M(x,y)为上任一点, MT为切线斜率为y', MN为法线,斜率为-I .'∠OMN=∠NMR
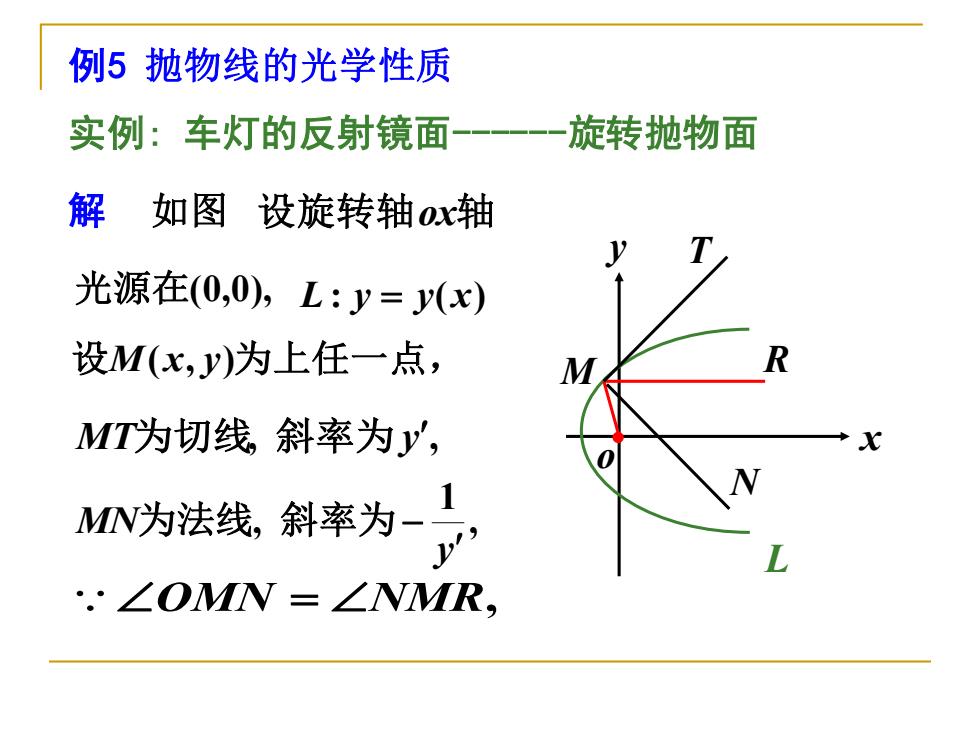
例5 抛物线的光学性质 实例: 车灯的反射镜面-旋转抛物面 解 如图 设旋转轴ox轴 光源在(0,0), L : y = y(x) 设M(x, y)为上任一点, MT为切线, 斜率为 y , , 1 , y MN 为法线 斜率为− OMN = NMR, x y o M T N R L
.'.tan∠OMN=tan∠NR, 由夹 tan∠OMN= 角正 1- 切公 式得 tan∠WMMR=I 得微分方程 y2+2-y=0,即y=-' 52+1. y
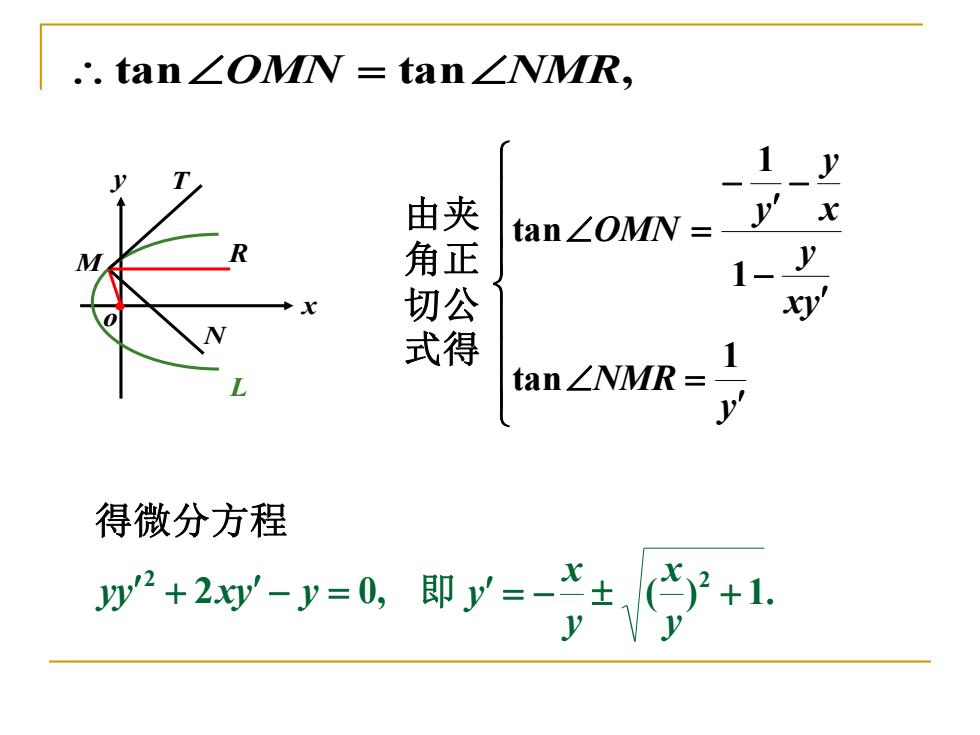
tanOMN = tanNMR, x y o M T N R L 由夹 角正 切公 式得 = − − − = y NMR xy y x y y OMN 1 tan 1 1 tan 得微分方程 2 0, 2 yy + xy − y = ( ) 1. 2 = − + y x y x 即 y

令u=上,得u+x -1±1+u2 W udu 分离变量 (1+u2)±V1+u2 tdt d 令1+u2=t2, t(t±1) 积分符m1生1-n 即2+1=C±1
令 , x y u = , 1 1 2 u u dx du u x − + 得 + = 分离变量 , (1 ) 1 2 2 x dx u u udu = − + + 令1+ u 2 = t 2 , , ( 1) x dx t t tdt = − 积分得 ln 1 ln , x C t = 1 1, 2 + = x C 即 u

平方化简得 .2C 代回w=,得 抛物线 y2=2C(x+) 所求旋转轴为ox轴的旋转抛物面方程为 广+=20x+ 以下介绍Malthus人口理论与Logistic模型
平方化简得 , 2 2 2 2 x C x C u = + 代回 , 得 x y u = ) 2 2 ( 2 C y = C x + 抛物线 所求旋转轴为ox轴的旋转抛物面方程为 ). 2 2 ( 2 2 C y + z = C x + 以下介绍Malthus人口理论与Logistic模型