
无穷级数习题课 习题课之二:函数项级数内容总结: 包括:函数项级数的一般概念; 和函数的求法; 幂级数的概念与函数展成泰勒级数
无穷级数习题课 习题课之二:函数项级数内容总结: 包括:函数项级数的一般概念; 和函数的求法; 幂级数的概念与函数展成泰勒级数
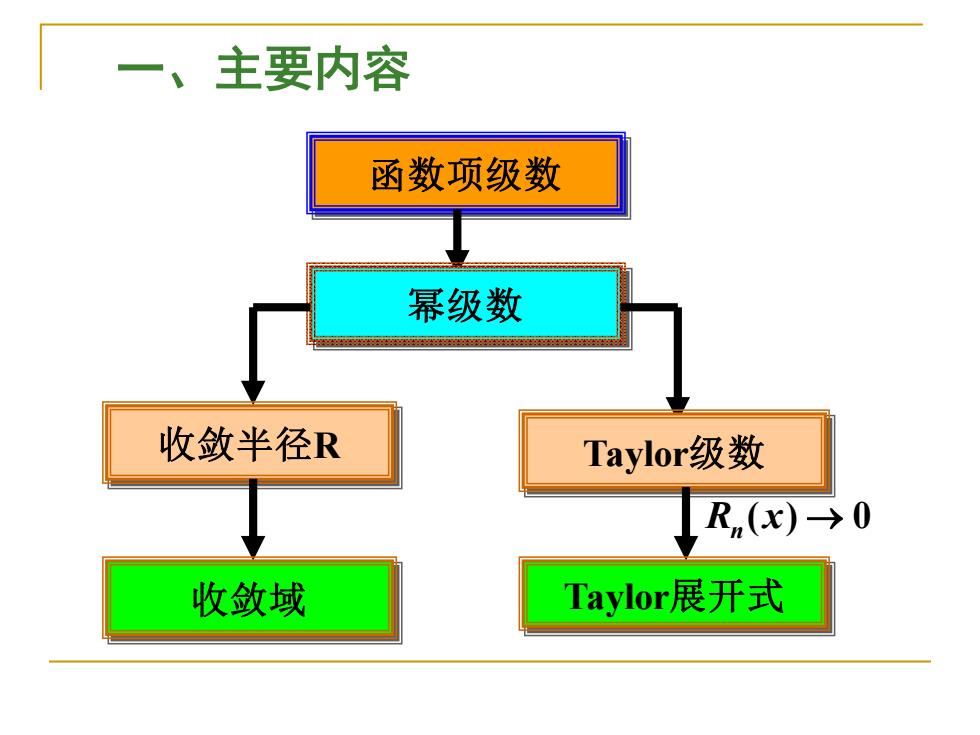
一、主要内容 函数项级数 幂级数 收敛半径R Taylora级数 Rn(x)→0 收敛域 Taylor展开式
一、主要内容 函数项级数 幂级数 收敛半径R 收敛域 Taylor级数 R (x) → 0 n Taylor展开式

1.幂级数 (1) 定义 00 形如∑4(x-)的级数称为幂级数。 n=0 当x。=0时, 其中an为幂级数系数. 1=( (2) 收敛性 对 ∑anx" 总存在正数R使得 n= 当xR时,幂级数发散;发散 收敛 发散 0 R
1.幂级数 (1) 定义 形如 n n an (x x ) 0 0 = − 的级数称为幂级数. 0 , 当x0 = 时 n n n a x =0 其中an为幂级数系数. (2) 收敛性 当 x R时,幂级数绝对收敛; 对 n=1 n n a x 总存在正数 R 使得 当 x > R时, 幂级数发散; −R O R x ( ) 发散 收 敛 发散

R一一收敛半径(一R,R)一一收敛区间 设 lim =p(或1ima,=p) n-→ooLn 1→00 (1) 则当p≠0时,R=;(2) 当p=0时,R=+oo; 3)当p=+w时,R=0. 注①形如∑anlp(x)的级数,求收敛域 应先求出 ∑ay 的收敛半径R Ip(x)KR一一原级数的收敛点
R--收敛半径(-R,R)--收敛区间 设 = + → n n n a a 1 lim (或 = → n n n lim a ) (1) 则当 0时, = 1 R ; (2) 当 = 0时,R = +; (3) 当 = +时,R = 0. 注 ①形如 n n a [(x)] 的级数,求收敛域 n n a y 的收敛半径R |(x)| R --原级数的收敛点 应先求出