
第十章 微分方程与差分方程 探索和研究变量与变量之间的关系是社会科学与 自然科学问题中所面临的重要课题。一般而言,变量 与变量之间有如下两种关系: 1、确定性关系 立方体的体积与边长之间的关系; 自由落体运动中距离与时间的关系等。 2、随机性关系 人的身高与体重之间的关系; 人的年龄与血压之间的关系等
第十章 微分方程与差分方程 探索和研究变量与变量之间的关系是社会科学与 自然科学问题中所面临的重要课题。一般而言,变量 与变量之间有如下两种关系: 1、确定性关系 立方体的体积与边长之间的关系; 自由落体运动中距离与时间的关系等。 2、随机性关系 人的身高与体重之间的关系; 人的年龄与血压之间的关系等

微分方程是寻求具有确定性关系的变量之间的 关系的科学; 概率论与数理统计则是研究具有随机性关系的 变量之间的关系的科学。 方程的概念: 代数方程一含有未知数的方程。 微分方程一含有未知函数的导数或微分的方程
微分方程是寻求具有确定性关系的变量之间的 关系的科学; 概率论与数理统计则是研究具有随机性关系的 变量之间的关系的科学。 方程的概念: 代数方程 — 含有未知数的方程。 微分方程 — 含有未知函数的导数或微分的方程
§10.1微分方程的基本概念 引例1一曲线通过点(1,2),在该曲线上任意点 处的切线斜率为2x,求该曲线的方程. dy 方程: =2x dx yx1=2 通解:y=x2+C 特解:y=x2+1
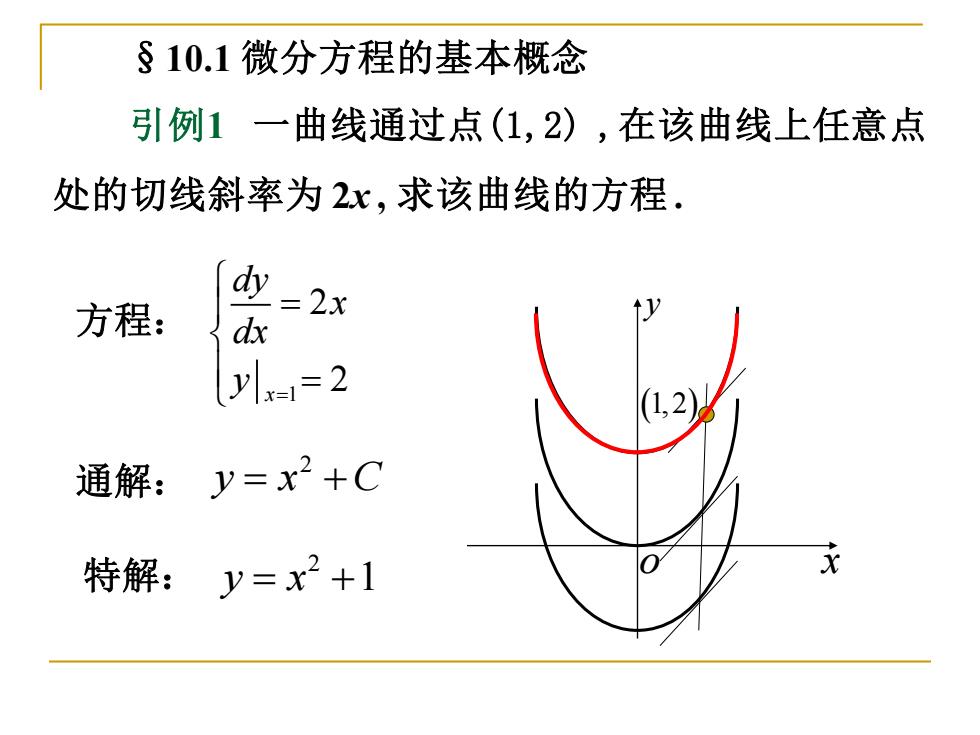
§10.1 微分方程的基本概念 引例1 一曲线通过点(1,2) ,在该曲线上任意点 处的切线斜率为 2x , 求该曲线的方程 . x y o 方程: 1 2 2 x dy x dx y = = = 通解: 2 y x C = + 特解: 2 y x = +1 (1, 2)

引例2列车在平直路上以20m/s的速度行驶, 制动时获得加速度a=-0.4m/s2,求制动后列车的 运动规律. d2s 方程: =-0.4 d:2 ds S=0=0, dtt=020 通解:s=-0.2t2+C1t+C2 特解:8=-0.2t2+20t
引例2 列车在平直路上以 的速度行驶, 制动时获得加速度 求制动后列车的 运动规律. 0 , s t=0 = 方程: 通解: 1 2 2 s = − 0.2t +C t +C 特解: s 0.2 t 20 t 2 = − +

定义1一个方程,如果含有未知函数的导数或 微分,则称该方程为微分方程;微分方程中出现的 未知函数的导数的最高阶数称为这个方程的阶.未知 函数是一元函数的微分方程称为常微分方程 未知函数是多元函数的微分方程,称为偏微分 方程 常微分方程(本章内容) 分类 偏微分方程
定义1 一个方程,如果含有未知函数的导数或 微分,则称该方程为微分方程;微分方程中出现的 未知函数的导数的最高阶数称为这个方程的阶. 未知 函数是一元函数的微分方程称为常微分方程. 未知函数是多元函数的微分方程,称为偏微分 方程. 常微分方程 偏微分方程 (本章内容) 分类

一般地,n阶常微分方程的形式是 F(x,yy',.,ym)=0 (1) 或 ym)=f(x,y,y,.,ym-)(n阶显式微分方程) 定义2如果将已知函数y=(x代入方程()后, 能使其成为恒等式,则称函数 y=逯对程(1)的 解. 定义3若微分方程的解中含有任意常数,且相互 独立的任意常数的个数与微分方程的阶数相同,则称 此解为微分方程的通解.如果微分方程的解中不含任 意常数,称这样的解为该微分方程的特解
( , , , , ) 0 ( ) = n F x y y y ( , , , , ) ( ) ( −1) = n n y f x y y y (n 阶显式微分方程) 一般地 , n 阶常微分方程的形式是 或 定义2 如果将已知函数 代入方程 (1)后, 能使其成为恒等式,则称函数 是方程(1) 的 解. y = (x) y = (x) (1) 定义3 若微分方程的解中含有任意常数,且相互 独立的任意常数的个数与微分方程的阶数相同,则称 此解为微分方程的通解.如果微分方程的解中不含任 意常数,称这样的解为该微分方程的特解.

定解条件一确定通解中任意常数的条件。 n阶方程的初始条件(或初值条件): (o)=%,(x)=%,yn-(xo)=- 2x d2y 引例1 x 引例2 dr2 =-0.4 yx==2 0=0,410=20 通解: y=x2+C s=-0.2t2+C1t+C2 特解:y=x2+1 s=-0.2t2+20t
0 , s t=0 = 20 d 0 d = t t= 引例2 s 0.4 2 2 d d = − x y ( 1) 0 0 ( 1) 0 0 0 0 ( ) , ( ) , , ( ) − − = = = n n y x y y x y y x y — 确定通解中任意常数的条件. n 阶方程的初始条件(或初值条件): x x y 2 d d = y x=1= 2 引例1 y = x +C 2 1 2 2 通解: s = −0.2t +C t +C s 0.2t 20t 2 1 = − + 2 特解: y = x + 定解条件
微分方程的解函数的图形是曲线,叫做微分方 程的积分曲线.通解表示一族积分曲线,特解表示 积分曲线族中某一条特定的曲线。 例3验证函数 y=C sin x+C2 cosx (C1,C,为任意常数)是方程 衣 y”+y=0的通解, 并求出满足初始条件以-=1,y儿=-1的特解
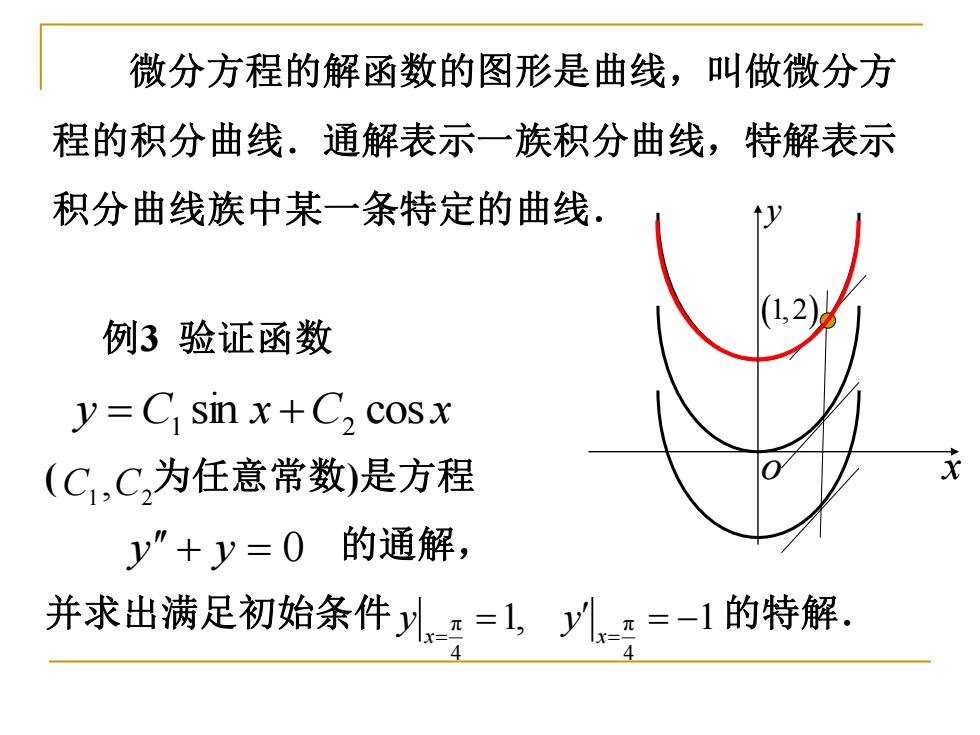
微分方程的解函数的图形是曲线,叫做微分方 程的积分曲线.通解表示一族积分曲线,特解表示 积分曲线族中某一条特定的曲线. x y o (1, 2) 例3 验证函数 ( 为任意常数)是方程 的通解, 并求出满足初始条件 的特解. y C sin x C cos x = 1 + 2 1 2 C ,C y + y = 0 π π 4 4 1, 1 x x y y = = = = −

§10.2可分离变量的微分方程与齐次方程 在本节和下一节的内容中,我们将讨论一些特 殊的一阶微分方程F(x,y,y)=0的解法, 一、可分离变量的微分方程 如果一个一阶微分方程能化成 dy =f(x)0y)→ g(y)dy=f(x)dx dr 的形式,则该方程就称为可分离变量的微分方程
§10.2 可分离变量的微分方程与齐次方程 F x y y ( , , 0 ) = 在本节和下一节的内容中,我们将讨论一些特 殊的一阶微分方程 的解法. 一、 可分离变量的微分方程 如果一个一阶微分方程能化成 的形式,则该方程就称为可分离变量的微分方程. ( ) ( ) d d f x y x y = g( y)dy = f (x)dx

例1求微分方程 d少=2的通解. dx 例2求微分方程 -x1+y2) dx (1+x2)y 满足初始条件yl0=1的特解, 例3求微分方程(1+y2)x-xy1+x2)dy=0 满足初始条件y()=2的特解
例1 求微分方程 xy x y 2 d d = 的通解. x y x y dx dy (1 ) (1 ) 2 2 + + = y | x=0 =1 例2 求微分方程 满足初始条件 的特解. 2 2 (1 )d (1 )d 0 + − + = y x xy x y y(1) = 2 例3 求微分方程 满足初始条件 的特解