
无穷级数习题课 习题课之二:函数项级数内容总结: 包括:函数项级数的一般概念; 和函数的求法; 幂级数的概念与函数展成泰勒级数
无穷级数习题课 习题课之二:函数项级数内容总结: 包括:函数项级数的一般概念; 和函数的求法; 幂级数的概念与函数展成泰勒级数
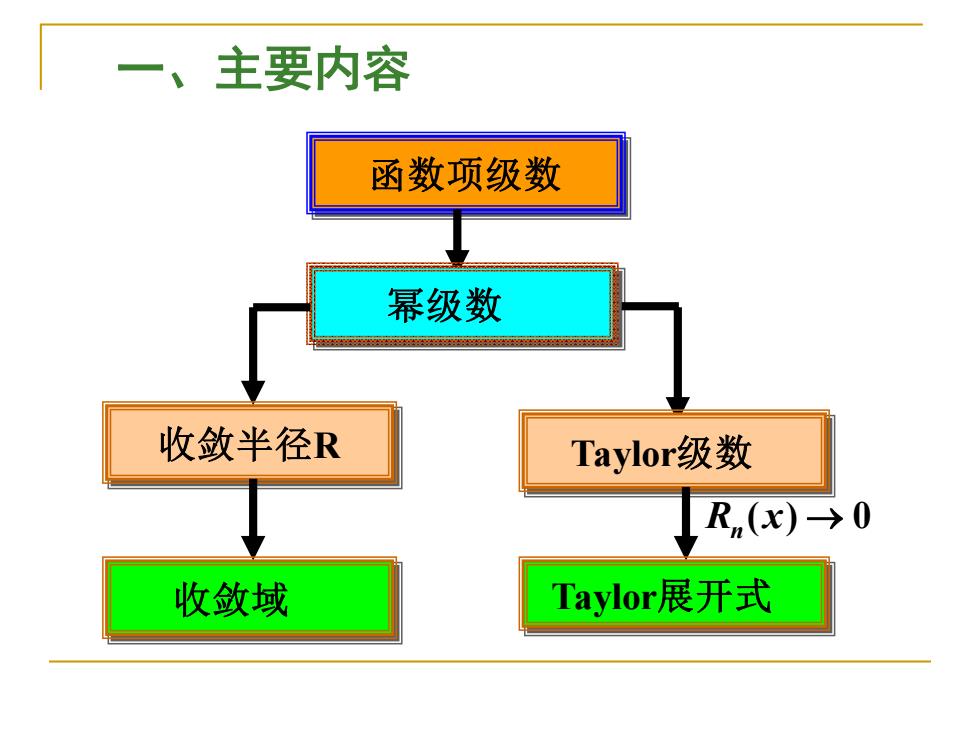
一、主要内容 函数项级数 幂级数 收敛半径R Taylor级数 R(x)→0 收敛域 Taylor展开式
一、主要内容 函数项级数 幂级数 收敛半径R 收敛域 Taylor级数 R (x) → 0 n Taylor展开式

一、幂级数 (1) 定义 0 形如∑4,(x-七)”的级数称为幂级数。 n=0 当x=0时, 其中,n为幂级数系数, 1= (2) 收敛性 0 对 ∑a,x 总存在正数R使得 =1 当xR时,幂级数发散;发散 收敛 发散
一、幂级数 (1) 定义 形如 n n an (x x ) 0 0 = − 的级数称为幂级数. 0 , 当x0 = 时 n n n a x =0 其中an为幂级数系数. (2) 收敛性 当 x R时,幂级数绝对收敛; 对 n=1 n n a x 总存在正数 R 使得 当 x > R时, 幂级数发散; −R O R x ( ) 发散 收 敛 发散

R一收敛半径,(-R,R)一收敛区间, 设 lim n+1 =p (或lim4yan=p) n→o n->co (1) 则当p≠0时,R=;(2) 当p=0时,R=+0; 0 (3)当p=+o时,R=0. 注①形如∑anlp(x”的级数,求收敛域 应先求出 ∑aJy 的收敛半径R |p(x)kR一-) 原级数的收敛点
R-收敛半径, (−R,R)-收敛区间. 设 = + → n n n a a 1 lim (或 = → n n n lim a ) (1) 则当 0时, = 1 R ; (2) 当 = 0时,R = +; (3) 当 = +时,R = 0. 注 ①形如 n n a [(x)] 的级数,求收敛域 n n a y 的收敛半径R |(x)| R --原级数的收敛点 应先求出

|p(x)>R一一原级数的发散点; 再研究|p(x)=R的点的敛散性。 ②用公式R=lima. 求收敛半径。 n-→oLn+1 n,n+1应是x”,x+1的系数,否则 可作代换或直接利用比值法或根值法来确定。 ③求出收敛半径后,必须用常数项级数审敛法判定 端点x=士R处的敛散性
|(x)|> R --原级数的发散点; 再研究 |(x)|= R ② 用公式 1 lim + → = n n n a a R 求收敛半径。 1 , n n+ a a 应是 1 , n n+ x x 的系数,否则 可作代换或直接利用比值法或根值法来确定. ③求出收敛半径后,必须用常数项级数审敛法判定 端点 x = R 处的敛散性。 的点的敛散性

(3)幂级数的运算 a.代数运算性质: R=minR,R2 b.和函数的分析运算性质: 和函数连续,逐项微分,逐项积分 收敛半径不变,端点的敛散性需要另行讨论
(3)幂级数的运算 a.代数运算性质: R = minR1 ,R2 b.和函数的分析运算性质: 和函数连续,逐项微分,逐项积分 收敛半径不变,端点的敛散性需要另行讨论

(4)幂级数求和函数 利用几个已知的展开式,如e,sinx,1,1+x)” 1±x 通过某些简单运算而求得 i.化成两个幂级数的和,差,积,商 ⅱ.作变量代换y=p(x) ⅱ.求导或积分 通项形如 x 先微分后积分; n 2n+1 通项形如x"-或(2n+1)x2m先积后微
(4) 幂级数求和函数 利用几个已知的展开式,如 1 1 1 ,sin , ,( ) x m e x x x + 通过某些简单运算而求得 ⅰ.化成两个幂级数的和,差,积,商 ⅱ.作变量代换 y = (x) ⅲ.求导或积分 通项形如 2 1 2 1 + + n x n x n n 或 先微分后积分; 通项形如 n n nx n x 1 2 (2 + 1) − 或 先积后微

步骤: ①求收敛域,设s(x)=∑a,x” n= 00 ②对s()=∑anx”进行运算 s(x)保留所有的运算记号 00 x“的运算结果要具体算出; n=] 化成易求和的形式 ③再进行上述运算的逆运算得s(x)
步骤: ①求收敛域,设 1 ( ) n n n s x a x = = ② 对 = = 1 ( ) n n s x an x 进行运算 s( x) 保留所有的运算记号 n=1 n an x 的运算结果要具体算出; 化成易求和的形式 ③ 再进行上述运算的逆运算得 s( x)

二、幂级数展开式 (1) 定义;(2)充要条件; (3)唯一性; (4)展开方法 a.直接法(泰勒级数法) 步骤: 0求a.=f2m=0,2,为 n! (2)讨论limR.=0或fm(x)≤M, 则级数在收敛区间内收敛于f(x)
二、幂级数展开式 (1) 定义; (2) 充要条件; (3) 唯一性; (4) 展开方法 a.直接法(泰勒级数法) 步骤: 0 1 0 1 2 ( )( ) ( ) ( , , , ); ! n n f x a n n 求 = = (2) lim 0 ( ) , ( ) R f x M n n n = → 讨论 或 则级数在收敛区间内收敛于 f (x)

b.间接法 根据唯一性,利用常见展开式,通过变量代换,四 则运算,恒等变形,逐项求导,逐项积分等方法,求展 开式. (5)几个常用的函数展开式 1 =1+x+x2+.+x”+.,x∈(-1,1) 1-x e*=1+x+ (-0<X<+0) 2! 十.+ x3,x5 sinx=x- 3!5! -+(02 (2n-1)! +.(0<x<+oo)
根据唯一性, 利用常见展开式, 通过变量代换, 四 则运算, 恒等变形, 逐项求导, 逐项积分等方法,求展 开式. b.间接法 (5) 几个常用的函数展开式 2 1 2 ( ) ! ! n x x x e x x n = + + + + + − + 1 2 1 1 1 1 , ( , ) n x x x x x = + + + + + − − 3 5 2 1 1 1 3 5 2 1 sin ( ) ( ) ! ! ( )! n x x x n x x x n − − = − + − + − + − + −