
§7.5多元函数的极值及其求法 上次课内容复习: 1、极值的定义; 2、函数取得极值的必要条件; 3、函数取得极值的充分条件; 4、求解函数极值的三个步骤; 5、求解函数最值的基本步骤
§7.5 多元函数的极值及其求法 1、极值的定义; 2、函数取得极值的必要条件; 3、函数取得极值的充分条件; 4、求解函数极值的三个步骤; 5、求解函数最值的基本步骤。 上次课内容复习:

三、条件极值 无条件极值:对自变量只有定义域限制 极值问题 条件极值:对自变量除定义域限制外, 还有其它条件限制 条件极值的求法: 方法1代入法.例如, 在条件p(x,y)=0下,求函数z=f(x,y)的极值 整从条件6x,)=0中解出y=w() 求一元函数z=f(x,W(x)的无条件极值问题
三、条件极值 极值问题 无条件极值: 条件极值 : 条件极值的求法: 方法1 代入法. 求一元函数 的无条件极值问题 对自变量只有定义域限制 对自变量除定义域限制外, 还有其它条件限制 例如 , 转 化 在条件(x, y) = 0下, 求函数 z = f (x, y)的极值 从条件(x, y) = 0中解出 y =(x) z = f (x,(x))

方法2拉格朗日乘数法.例如, 在条件p(x,y)=0下,求函数z=f(x,y)的极值 如方法1所述,设p(x,y)=0可确定隐函数y=yW(x), 则问题等价于一元函数z=f(x,W(x)的极值问题,故 极值点必满足 d=fx+fy dx =0 d 因 y=_9 Px-0 dx ,故有fx-y 记 Px Py
在条件(x, y) = 0下, 方法2 拉格朗日乘数法. 如方法1所述 , 则问题等价于一元函数 可确定隐函数 的极值问题, 极值点必满足 设 记 求函数 z = f (x, y)的极值. (x, y) = 0 y =(x), z = f (x,(x)) 例如, 故 0 d d d d = + = x y f f x z x y , d d y x x y 因 = − − = 0 y x x y f f y y x x f f = 故有 =−

fx+元0x=0 极值点必满足 fy+元0y=0 p(x,y)=0 引入辅助函数 L=f(x,y)+九0(x,y) L=f+2p.=0 则极值点满足: L,=∫,+元9,=0 人L2=0=0 辅助函数L称为拉格朗日(Lagrange)函数.利用拉格 朗日函数求极值的方法称为拉格朗日乘数法
引入辅助函数 辅助函数L 称为拉格朗日( Lagrange )函数.利用拉格 极值点必满足 + = 0 x x f + = 0 y y f (x, y) = 0 则极值点满足: 朗日函数求极值的方法称为拉格朗日乘数法. L f x y x y = + ( , ) ( , )

推广 拉格朗日乘数法可推广到多个自变量和多 个约束条件的情形 例如,求函数u=f(x,y,z)在条件p(x,y,z)=0, W(x,y,z)=0下的极值. 设L=f(x,y,z)+p(x,y,2)+2(x,y,) Lx=f+乃p+入29x=0 L,=f+八9,+九24,=0 解方程组 L=f+入p.+九2必2=0 L%,=9=0 可得到条件极 L2,==0 值的可疑点
推广 拉格朗日乘数法可推广到多个自变量和多 个约束条件的情形. 设 解方程组 可得到条件极 值的可疑点 . 例如, 求函数 下的极值. u = f (x, y,z) 在条件 (x, y,z) = 0, (x, y,z) = 0 1 2 L f x y z x y z x y z = + + ( , , ) ( , , ) ( , , )
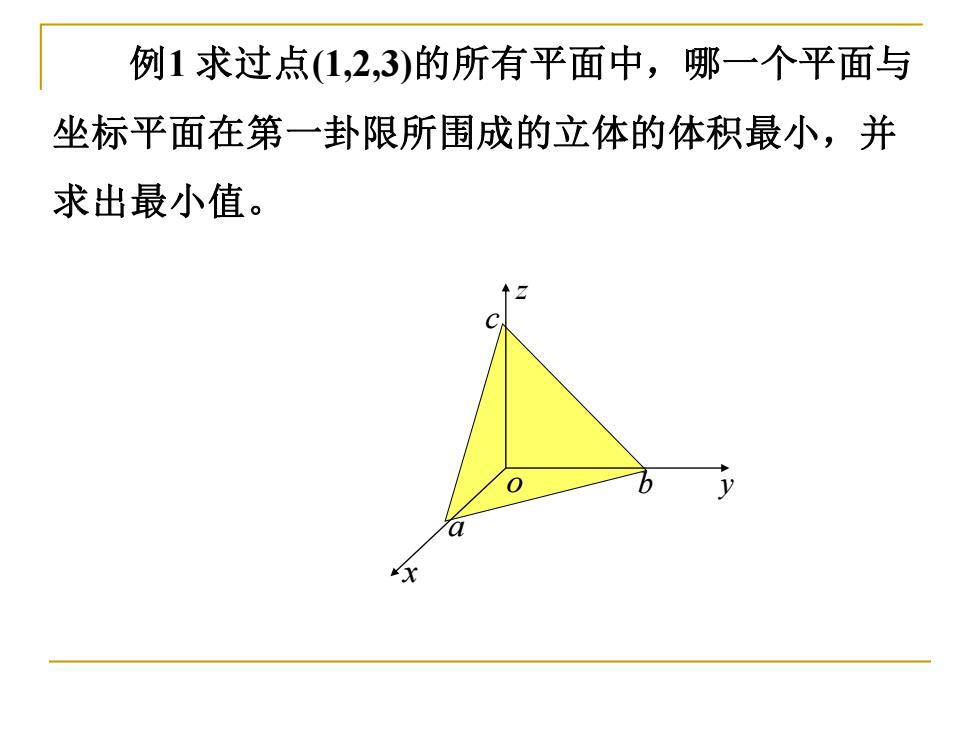
例1求过点1,2,3)的所有平面中,哪一个平面与 坐标平面在第一卦限所围成的立体的体积最小,并 求出最小值。 ↑2
a b c 例1 求过点(1,2,3)的所有平面中,哪一个平面与 坐标平面在第一卦限所围成的立体的体积最小,并 求出最小值。 x o y z
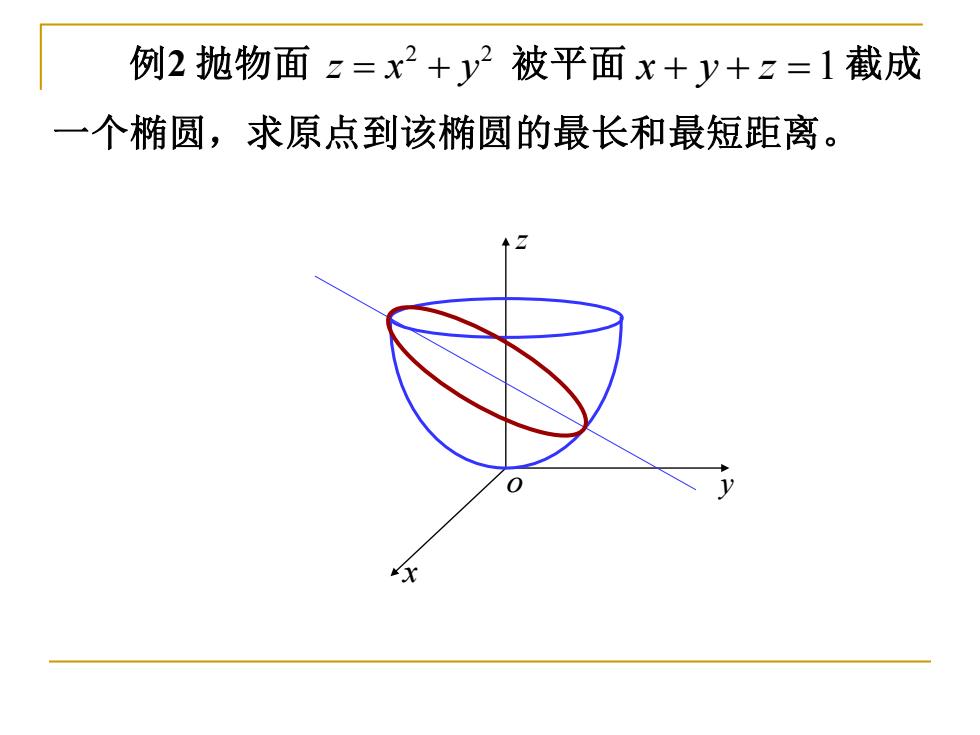
例2抛物面z=x2+y2被平面x+y+z=1截成 一个椭圆,求原点到该椭圆的最长和最短距离
例2 抛物面 被平面 截成 一个椭圆,求原点到该椭圆的最长和最短距离。 2 2 z x y = + x y z + + =1 x o y z

思考与练习 已知平面上两定点A(1,3),B(4,2), 试在椭圆 +广-1>0,y>0圆周上求-点C使 4 △ABC面积S最大 解答提示:设C点坐标为(x,y), D 则sa=)店×4C E i 1-2 3 -1 ko x-1y-3 -0.0+3y-10y 0 1 三一 x+3y-10
已知平面上两定点 A( 1 , 3 ), B( 4 , 2 ), 试在椭圆 圆周上求一点 C, 使 △ABC 面积 S△最大. 解答提示: C B A o y E x 设 C 点坐标为 (x , y), D 思考与练习 1 3 0 3 1 0 − − − x y i j k (0, 0, 3 10) 2 1 = x + y − 1 ( 0, 0) 9 4 2 2 + = x y x y 则 3 10 2 1 = x + y −

设拉格朗日函数F=(x+3y-10)2+2(1 2(x+3y-10)-2 x=0 解方程组 6x+3y-10)- 2元 4)=0 12 2-0 9 点击图中任意点 画开始或暂停 3 得驻点x= 5y 5对应面积S1.646 而SD=2,Sc=3.5,比较可知,点C与E重合时, 三角形面积最大
设拉格朗日函数 解方程组 得驻点 对应面积 而 比较可知, 点 C 与 E 重合时, 三角形面积最大. ) 9 4 ( 3 10) (1 2 2 2 x y F = x + y − + − − 0 9 2 2(x + 3y −10) − x = 0 4 2 6(x + 3y −10) − y = 0 9 4 1 2 2 − − = x y , S 1.646 5 4 , 5 3 x = y = SD = 2, SC = 3.5, 点击图中任意点 动画开始或暂停

本节内容小结 EX7-64,5,6,7. 1.函数的极值问题 第一步利用必要条件在定义域内找驻点. 如对二元函数z=f(x,y),即解方程组 (x,y)=0 1f(x,y)=0 第二步利用充分条件判别驻点是否为极值点. 2.函数的条件极值问题 ()简单问题用代入法 (2)一般问题用拉格朗日乘数法
本节内容小结 1. 函数的极值问题 第一步 利用必要条件在定义域内找驻点. 即解方程组 第二步 利用充分条件 判别驻点是否为极值点 . 2. 函数的条件极值问题 (1) 简单问题用代入法 z = f (x, y), = = ( , ) 0 ( , ) 0 f x y f x y y x 如对二元函数 (2) 一般问题用拉格朗日乘数法 EX 7-6 4,5,6,7