
二、导数的计算 1.讨论函数在x=0的极限、连续、可导性 sin ,x≠0 0 x=0 分情况讨论:4≤0,01' a=2e,b=-e
二、导数的计算 1 sin , 0 ( ) 0, 0 x x f x x x = = 1. 讨论函数在 x = 0 的极限、连续、可导性 分情况讨论: 0, 0 , 1 , 2 2 , 1 ( ) , , , ( ) . , 1 x e x f x a b f x ax b x = + 设函数 取何值时 为可导函数 a e b e = = − 2

sinx,x<0 1.若y= ,求y' X, x≥0 2.求由方程 x3+y3-3xy=0确定的隐函数 y=y(x)的导数 dx 3设-acos月=cos,0<a≤1三6<子求 42 4.己知 y+2 5. dx Jo 1+t2
sin , 0 , 0 x x y x x = y ' 1. 若 , 求 . 0 cos , cos ,0 2 t x a udu y b t a t b = = 2 2 d y dx 3. 设 ,求 2 5 2 x y x − = + 4.已知 , 求 dy . 3 0 3 3 x + y − xy = y = y(x) dx dy 2. 求由方程 确定的隐函数 的导数 sin 0 2 1 1 d x dt dx t = + 5.

设某厂每批生产某种商品的固定成本为200(百元) 每生产一个单位产品,成本增加5(百元),已知需求函 数 Q=100-2p (其中为价格Q为产量),这种产品在市场上是畅销的。 a.试分别列出该商品的总成本函数C(p)和总收益函数 R(p)的表达式。 b.求出使该商品的总利润最大的产量和最大利润。 c.求出需求弹性
Q =100 − 2 p C( p) R( p) 设某厂每批生产某种商品的固定成本为200(百元) 每生产一个单位产品,成本增加5(百元),已知需求函 数 a.试分别列出该商品的总成本函数 和总收益函数 b. 求出使该商品的总利润最大的产量和最大利润。 c. 求出需求弹性。 (其中 p 为价格, Q 为产量),这种产品在市场上是畅销的。 的表达式

a.总成本函数为: C(p)=200+59=700-10p 总收益函数为:R(p)=p·Q=100p-2p2 b.总利润函数为: L(p)=R(p)-C(p)=-2p2+110p-700,L'(p)=-4p+110 令 L(p)=0,得:p=27.5,Q=45。而L(27.5)=-4<0, 所以当产量为45时,总利润最大。 c.需求弹性:7=-p Q'(p) 2p (p) 100-2p
C p Q p ( ) 200 5 700 10 = + = − 2 R( p) = pQ =100 p − 2p a. 总成本函数为: 总收益函数为: b. 总利润函数为: 2 L p R p C p p p L p p ( ) ( ) ( ) 2 110 700; ( ) 4 110 = − = − + − = − + 令 ( ) 0, 27.5, 45 (27.5) 4 0, ' '' L p = 得:p = Q = 。而L = − 所以当产量为45时,总利润最大。 c.需求弹性: ( ) 2 ( ) 100 2 Q p p p Q p p = − = −

1.某厂每天生产某种产品9件的成本函数为 C(q)=0.5g2+36g+9800(元). 为使平均成本最低,每天产量应为多少?此时, 每件产品平均成本为多少?(6分) 产量q=140件,平均成本176元
q ( ) 0.5 36 9800 2 C q = q + q + 1. 某厂每天生产某种产品 件的成本函数为 为使平均成本最低,每天产量应为多少?此时, 每件产品平均成本为多少?(6分) (元). 产量 q =140件,平均成本176元
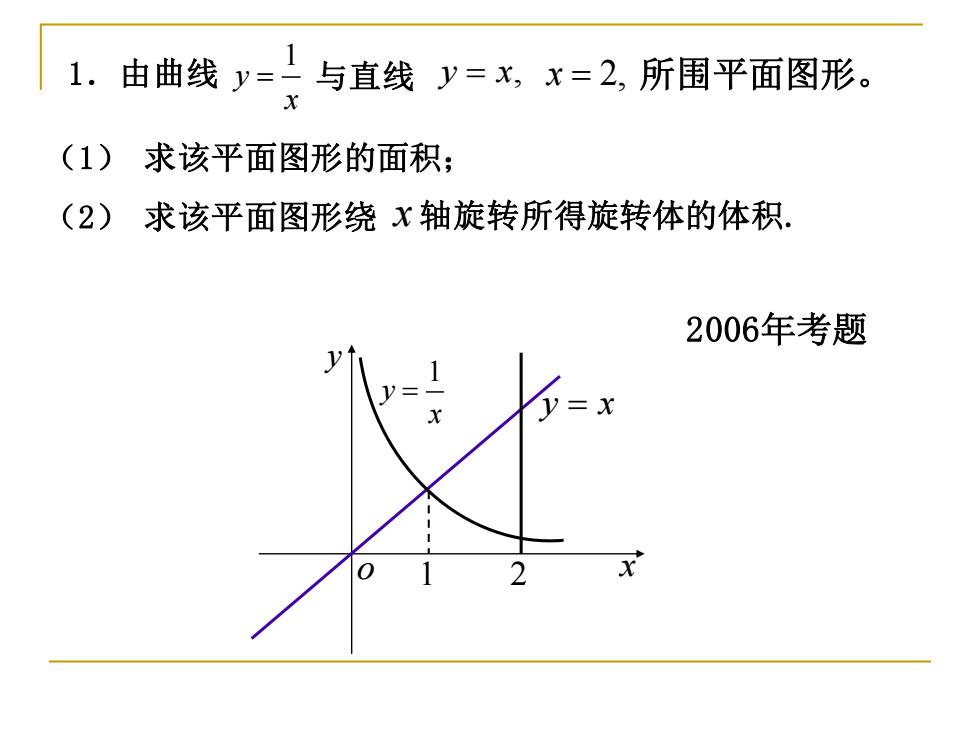
1.由曲线y=二与直线y=x,x=2,所围平面图形。 (1) 求该平面图形的面积; (2)求该平面图形绕x轴旋转所得旋转体的体积. 2006年考题 v=x
1 y x 1.由曲线 = 与直线 y x = , x = 2, x (1) 求该平面图形的面积; (2) 求该平面图形绕 轴旋转所得旋转体的体积. 所围平面图形。 x y o y x = 1 y x = 1 2 2006年考题

求不定积分 [I(x+x2+1)dx 实买分4 aa n时-gny*-i +nrf时1
ln( x + x +1)dx 求不定积分 2 1 2 0 (1 ) x xe dx + x 计算定积分 1 1 1 2 2 0 0 0 1 1 1 1 2 2 0 0 0 0 1 1 2 2 0 0 ( 1 1) (1 ) (1 ) (1 ) (1 ) (1 ) (1 ) (1 ) 1 (1 ) (1 ) 2 x x x x x x x x x xe x e e dx dx dx xxx e de e e dx dx x x x x e e e dx dx x x + − = = − +++ − = − = + + + + + − = − + +

”* 设 dx 五.证明题(5分) x>0,x2>0设f"(x)0,x2>0有 f(x+x2)<f(x)+f(x2)
2 2 2 1 . 4 t t x e d y y e dx = + = 设 ,求 1 2 x x 0, 0 f x f ( ) 0 , (0) 0 = 1 2 x x 0, 0 1 2 1 2 f x x f x f x ( ) ( ) ( ) + + 五.证明题(5分) 设 证明对任意的 有