
第四章不定积分 微分法:F'(x)=(?) 互逆运算 积分法:(?)'=f(x) §4.1不定积分的概念与性质 一、原函数与不定积分的概念 二、 基本积分表 三、不定积分的性质
第四章 不定积分 微分法: F(x) = ( ? ) 积分法: ( ? ) = f (x) 互逆运算 二、 基本积分表 三、不定积分的性质 一、 原函数与不定积分的概念 §4.1 不定积分的概念与性质

一、原函数与不定积分的概念 定义1如果在区间I上,可导函数F(x)的导函数 为f(x),即对任一x∈I,都有 F'(x)=f(x)或dF(x)=f(x)dx’ 那末函数F(x)就称为f(x)(或f(x)dx)在区间I 上的原函数。 例如:因为 (sinx)'=cosx (sinx+C)'=cosx (其中C是任意常数),所以sinx与sinx+C都是 cosx的原函数
一、原函数与不定积分的概念 定义1 如果在区间 I 上,可导函数 F x( ) 的导函数 为 f x( ) ,即对任一 x I ,都有 F x f x '( ) ( ) = 或 d ( ) ( )d F x f x x = , 那末函数 F x( ) 就称为 f x( ) (或 f x x ( )d )在区间 I 上的原函数。 (sin ) cos x x = (sin ) cos x C x + = sin x sin x C+ cos x 例如:因为 与 都是 的原函数. (其中 C 是任意常数),所以

问题: 1.在什么条件下,一个函数的原函数存在? 2.若原函数存在,它如何表示? 结论一(原函数存在定理):如果函数∫(x)在区 间I上连续,则f(x)在区间上一定有原函数,即存在 区间I上的可导函数F(x),使得对任一x∈I,有 F'(x)=f(x)
问题: 1. 在什么条件下, 一个函数的原函数存在 ? 2. 若原函数存在, 它如何表示 ? 结论一(原函数存在定理):如果函数 在区 间I上连续,则 在区间I上一定有原函数,即存在 区间I上的可导函数 ,使得对任一 ,有 f x( ) f x( ) F x( ) x I F x f x ( ) ( ) =

结论二:如果f(x)在区间I上有一个原函数F(x) 则:(1)F(x)+C(其中C为任意常数)都是f(x)的原 函数,即f(x)有无穷多个原函数; (2)如果G(x)是f(x)在区间上的另一个原函数, 则 秤x) 莲为常数,即 F(x)-G(x)=C(C为常数) (3)F(x)+C(C为任意常数)可以表达f(x)的 任意一个原函数
结论二:如果 在区间 上有一个原函数 则:(1) (其中 为任意常数)都是 的原 函数,即 有无穷多个原函数; (2)如果 是 在区间I上的另一个原函数, 则 和 之差为常数,即 (C为常数) (3) (C为任意常数)可以表达 的 任意一个原函数。 f x( ) I F x( ) F x C ( ) + C f x( ) f x( ) F x( ) G x( ) G x( ) f x( ) F x G x C ( ) ( ) − = F x C ( ) + f x( )

定义2f(x在区间I上的原函数全体称为f(x)在I 上的不定积分,记作f(x)dx,其中 ∫一积分号; f(x)一被积函数; x—天 积分变量;f(x)x一被积表达式, 若F'(x)=f(x),则 「f(x)dx=F(x)+C(C为任意常数) 例如, [e*dx=e*+C C称为积分常数 「x2dx=3x3+C 不可丢! sinxdx =-cosx+C
定义 2 在区间 I 上的原函数全体称为 上的不定积分, 其中 — 积分号; — 被积函数; — 积分变量; — 被积表达式. 若 则 ( C 为任意常数 ) C 称为积分常数 不可丢 ! 例如, = e x x d e C x + = x dx 2 x +C 3 3 1 记作 = sin xdx − cos x +C
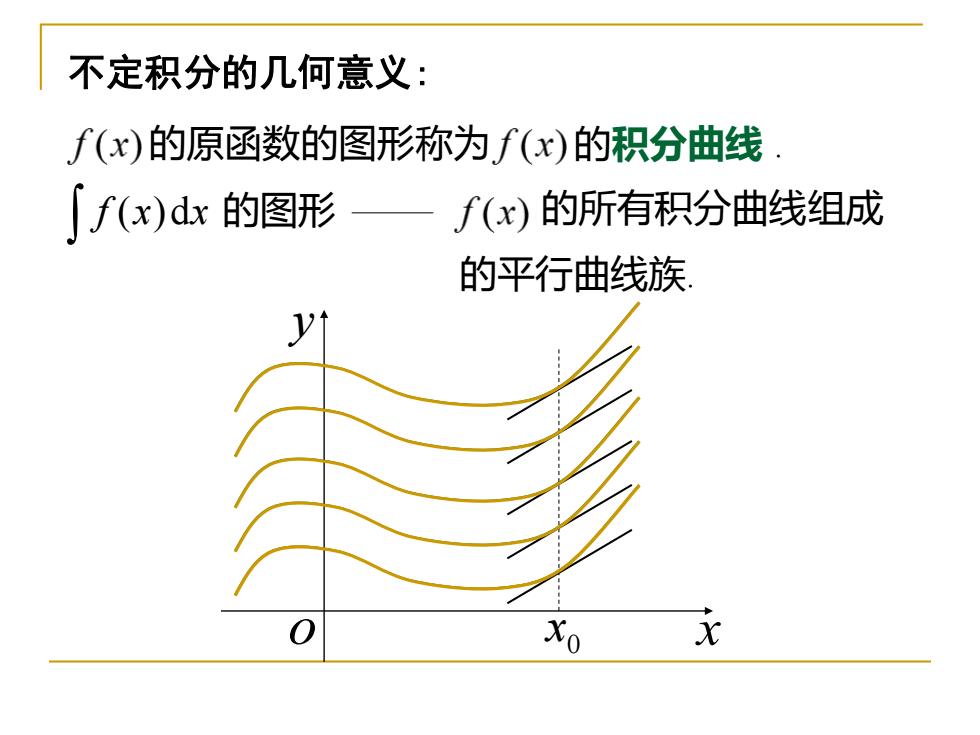
不定积分的几何意义: f(x)的原函数的图形称为f(x)的积分曲线 「f(x)dx的图形一 f(x)的所有积分曲线组成 的平行曲线族 Xo
不定积分的几何意义: 的原函数的图形称为 f (x)dx 的图形 的所有积分曲线组成 的平行曲线族. y o x0 x 的积分曲线
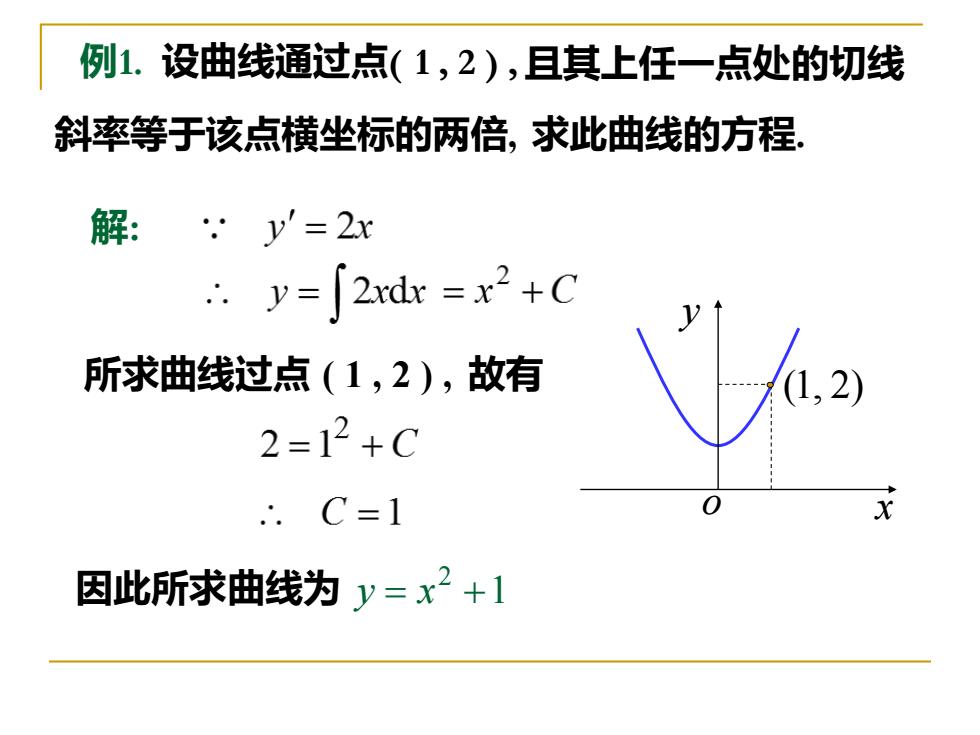
例1.设曲线通过点(1,2),且其上任一点处的切线 斜率等于该点横坐标的两倍,求此曲线的方程, 解:y'=2x .y=∫2de=x2+C 所求曲线过点(1,2),故有 2=12+C .C=1 因此所求曲线为y=x2+1
例1. 设曲线通过点( 1 , 2 ) , 且其上任一点处的切线 斜率等于该点横坐标的两倍, 求此曲线的方程. 解: 所求曲线过点 ( 1 , 2 ) , 故有 因此所求曲线为 1 2 y = x + y o x (1, 2)

二、 基本积分公式 利用逆向思维 ()「kdx=kx+C (k为常数) (2)∫xdr=x++C (4≠-1) x<0时 (3) (x)=[In(-x)-1 (4) dx 2 = arctanx+C -arccot x+C 1+x1 dx (5) arcsinx+C-arccosx+C /1-x
二、 基本积分公式 利用逆向思维 = (1) kdx kx +C ( k 为常数) = (2) x dx x +C + + 1 1 1 = x d x (3) ln x +C x 0时 ( −1) (ln x ) = [ln(−x)] x 1 = = + 2 1 d (4) x x arctan x +C 或 − arccot x +C = − 2 1 d (5) x x arcsin x +C 或 − arccos x +C

(6)cos xdx=sinx+C (7)J∫sinxdx=-cosx+C 肉,a2=tm-C 9∫,ja-am+c (10) secxtan xdx secx+C (11) csc x cot xdx=-cscx+C (12) ∫e'dr=e'+C
= x x 2 cos d (8) = sec xdx 2 tan x +C = (7) sin xdx − cos x +C = x x 2 sin d (9) = csc xdx 2 − cot x +C = (6) cos xdx sin x +C = (10) sec x tan xdx sec x +C = (11) csc x cot xdx − csc x +C = e x x (12) d e C x +
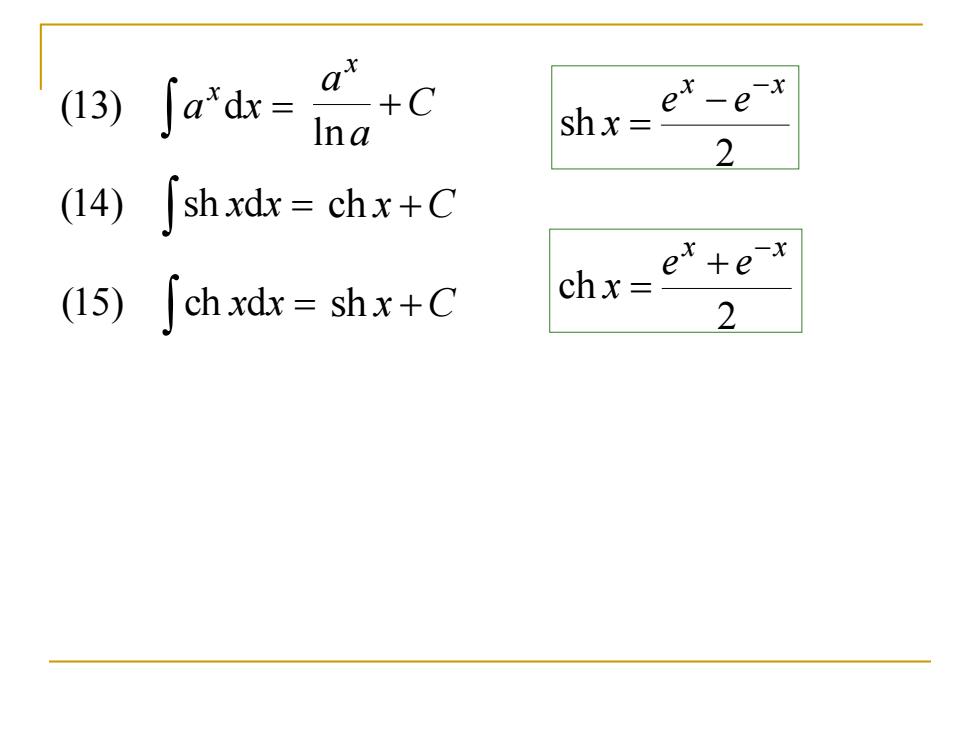
(13) [a"dx= ex-ex shx= 2 I4)∫shxdx=-chx+C (I5)「ch xdx=shx+C chx= 2
= a x x (13) d C a a x + ln 2 sh x x e e x − − = ch x +C = (15) ch xdx sh x +C = (14) sh xdx 2 ch x x e e x − + =