
上次课内容复习: (1)罗尔Rolle)中值定理。 (2)拉格朗日(Lagrange)中值定理。 (3)如果f'(x)=0,x∈I,→f(x)=constant,x∈I. (4)如果f'(x)≡g'(x),x∈I,→f(x)=g(x)+C,x∈I. (5)柯西(Cauchy)中值定理
上次课内容复习: (1)罗尔(Rolle)中值定理 。 (2)拉格朗日(Lagrange)中值定理。 (3)如果 f x x I f x x I ( ) 0, , ( ) constant, . = (4)如果 f x g x x I f x g x c x I ( ) ( ), , ( ) ( ) , . = + (5)柯西(Cauchy)中值定理

本次课内容: 运用柯西中值定理研究未定式的 极限问题(洛必达法则)。 函数之商的极限mf9(或” 袼必达,G.F.-A.de 0 型) 洛必达(1661- g(x)` 0 00 1704)法国数学家, 他著有《无穷小 转化 洛必达法则 分析》,并在该书 中提出了求未定 导数之商的极限im f'(x) 式极限的方法,后 8'(x) 人将其命名为 《洛必达法则
函数之商的极限 导数之商的极限 转化 ( 或 型) 洛必达法则 本次课内容: 运用柯西中值定理研究未定式的 极限问题(洛必达法则)。 . 洛必达(1661– 1704)法国数学家, 他著有《无穷小 分析》,并在该书 中提出了求未定 式极限的方法,后 人将其命名为 “洛必达法则

柯西(Cauchy)中值定理 如果函数f(x),F(x)满足如下条件: (1)在闭区间[a,b]上连续; (2)在开区间(a,b)内可导; (3)F(x)≠0, 则在(a,b)内至少有一点5,使得 f(b)-f(a_f'(5) F(b)-F(a)F()
如果函数 f x F x ( ), ( ) 满足如下条件: ( ) ( ) ( ) ( ) ( ) ( ) f b f a f F b F a F − = − 。 柯西(Cauchy)中值定理 (1) 在闭区间 上连续; (2) 在开区间 内可导; (3) 则在 内至少有一点 ,使得 [ , ] a b ( , ) a b ( , ) a b F x( ) 0,

§3.2洛必达(L'Hospital)法则 定理1若函数f(x)和g(x)满足: 1.lim f(x)=lim g(x)=0 2、在点x,的某去心邻域U°(x)内两者都可导, 且g'(x)≠0: 3、1im'因=A(何为实数,也可为士o或o); *68'(x) 则 lim)=lim= x6g(x)x→g'(x)
定理1 若函数 和 满足: 1、 ; 2、在点 的某去心邻域 内两者都可导, 且 ; 3、 ; f x( ) g x( ) 0 0 lim ( ) lim ( ) 0 x x x x f x g x → → = = 0 x 0 ( ) o U x g x ( ) 0 0 ( ) lim ( ( ) x x f x A A → g x = 可为实数,也可为 或 ) 则 0 0 ( ) ( ) lim lim ( ) ( ) x x x x f x f x A → → g x g x = = 。 §3.2 洛必达(L’Hospital)法则

推论1定理1中x→x。换为下列过程之一: x→x),X>X,X→0,X→+0,x→-00 条件2作相应的修改,定理1仍然成立。 推论2.若1m仍属型,且f(x),8) g'(x) 满足定理1的条件,则 lim-lim)=lim( 8(x) g(x) g"(x)
推论1 定理1中 0 x x → 换为下列过程之一: 0 x x , → − 条件2作相应的修改 , 定理1仍然成立。 x → +, 推论2. 若 ( ) lim ( ) f x g x 仍属 型, 且 ( ), ( ) 0 0 f x g x 满足定理1的条件,则
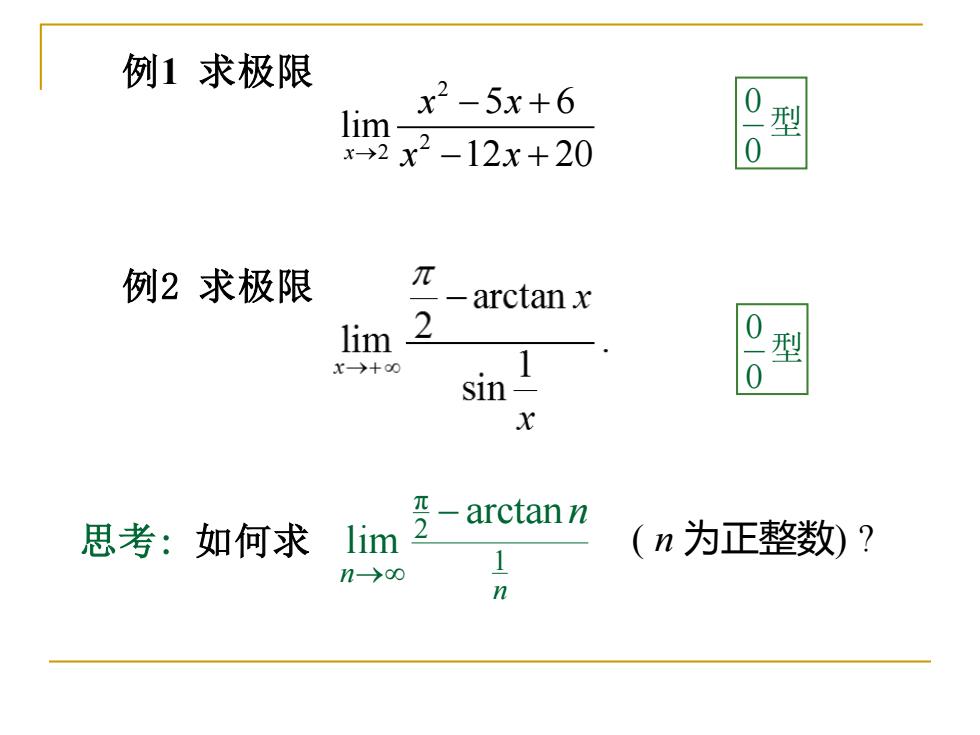
例1求极限 x2-5x+6 9x-12x+20 0 型 0 例2求极限 π arctan x lim 2 型 X→+0 sin- 0 X 一 arctann 思考:如何求 lim 2 (n为正整数)? n->oo 1 n
例2 求极限 型 0 0 例1 求极限 2 2 2 5 6 lim x 12 20 x x → x x − + − + 型 0 0 思考: 如何求 n n n 1 2 π arctan lim − → ( n 为正整数) ?

定理2若函数f(x)和g(x)满足: 1.lim f(x)=o0,limg(x)=o 2、M为正数,当x>M时,都有f'(x)及g(x) 存在,且g'(x)≠0; 3、 limM) A(4可为实数,也可为±士o或0) r∞g'(x) 则 limf)=lim =A。 x-→08(x) x→0g'(x) 对于其它变化过程也有类似的结论
对于其它变化过程也有类似的结论。 定理2 若函数 和 满足: 1、 ; 2、 M 为正数,当 时,都有 及 存在,且 ; 3、 f x( ) g x( ) lim ( ) ,lim ( ) x x f x g x → → = = g x ( ) 0 ( ) lim ( ( ) x f x A A → g x = 或 ) 则 ( ) ( ) lim lim ( ) ( ) x x f x f x A → → g x g x = = 。 x M f x ( ) g x ( ) 可为实数,也可为

In x 例3求极限 lim 00 型 r)+00 oo 例4求极限 m。6>0.>0 型 0 例5求极限 x+sinx 00 lim 型 x 00 特别说明: m不存在(≠0)时,不能用洛必达法则: li F'(x)
例3 求极限 型 例4 求极限 lim ( 0 , 0). e s x x x s →+ 型 例5 求极限 sin lim x x x →+ x + 型 ( ) , 不能用洛必达法则 ! ( ) ( ) lim 不存在 时 F x f x 特别说明:

其他未定式: 000,00-00,00,1,0°型 解决方法: 00 通分 取倒数 取对数 0.00 100 转化 转化 转化 0 00 00 例6求极限limx”lnx. 000型 x>01 例7求极限位 00-00型
其他未定式: 解决方法: 通分 转化 0 0 0 取倒数 转化 0 0 1 0 取对数 转化 − 0 lim ln . n x x x 例 → + 6 求极限 0型 例7 求极限 1 −型 1 1 lim x→ ln 1 x x − −
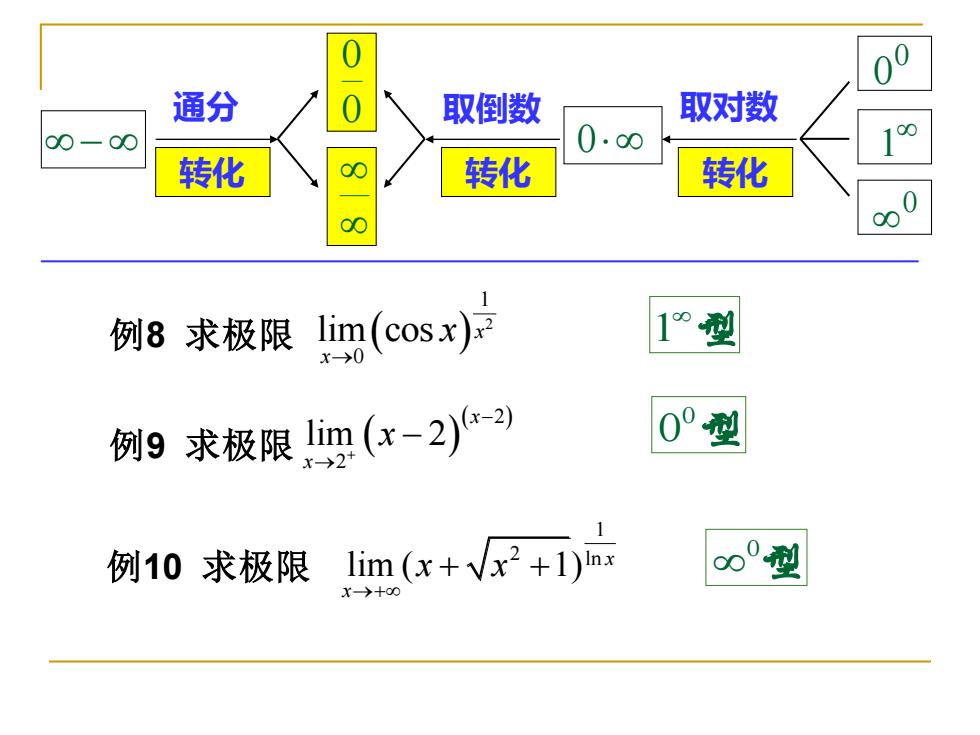
00 通分 取倒数 取对数 00-00 0.00 100 转化 转化 转化 0 00 例8求极限lim(cosx) 1型 例9求极限(-2)-) 0°型 例10求极限lim(x+V2+1) 000型
通分 转化 0 0 0 取倒数 转化 0 0 1 0 取对数 转化 − 例8 求极限 ( ) 2 1 0 lim cos x x x → 1 型 例10 求极限 1 2 ln lim ( 1) x x x x →+ + + 0 型 例9 求极限 ( ) ( 2) 2 lim 2 x x x + − → − 0 0 型