
第一章 函数与极限 §1.2函数的极限 一、数列的极限 二、函数的极限 极限是微积分学的灵魂,极限思想贯穿 于微积分学的始终
§1.2 函数的极限 一、数列的极限 第一章 函数与极限 二、函数的极限 极限是微积分学的灵魂,极限思想贯穿 于微积分学的始终

一、数列的极限 数列的概念: 一列(无穷多个)有序的数x,x2,.,m,.称为 数列。x称为通项(一般项) 定义:自变量取正整数的函数称为数列,记作 xn=f(n)或{xn}.xn称为通项(一般项). 1 例1设数列xn=二, n=1,2,. 考察:当n→o,xn→?即求limx
一、数列的极限 定义:自变量取正整数的函数称为数列,记作 或 称为通项(一般项) . 数列的概念: 一列(无穷多个)有序的数 1 2 , , , , n x x x 称为 数列。 称为通项(一般项) 。 例1 设数列 1 , 1,2, n x n n = = 考察:当 , ? n n x → → 即求 lim n n x →

例2设数列 x=(-10” n=1,2,. 之 考察:当noo,x,→?即求limx。 n00 例3 设数列x,=1-() n=1,2,. 2n 考察:当n→o,xn→?即求lim x。 通过以上三例的讨论,你能够得到 什么启示?
例2 设数列 ( ) 1 1 , 1, 2, n n x n n = − = 考察:当 , ? n n x → → 即求 lim n n x → 。 例3 设数列 1 ( 1) , 1,2, 2 n n x n n − − = = 考察:当 , ? n n x → → 即求 lim n n x → 。 通过以上三例的讨论,你能够得到 什么启示?

定义1设有数列{xn},如果存在常数a,对 于任意给定的正数£(无论它多小),总存在正整 数N,使得对于n>N的一切xn,不等式xn-aoo xn→an→o). 如果不存在这样的常数a,则称数列{xn}没有 极限,或称数列{xn}发散,习惯上也称limx不 n-co 存在
定义1 设有数列 ,如果存在常数 ,对 于任意给定的正数 (无论它多小),总存在正整 数 ,使得对于 的一切 ,不等式 都成立,则称常数 为数列 的极限,或者称数 列 收敛 ,且收敛于 ,记作 ,或 . xn a N n N n x x − a n xn a xn a xn a n = → lim x → a(n → ) n 如果不存在这样的常数 ,则称数列 没有 极限,或称数列 发散,习惯上也称 不 存在. xn xn lim n n x → a

数列极限的E-N定义 s>0,正数N,当n>N时,总有xn-aoo a-£N) 几何解释: 即xn∈U(a,e) (n>N) 0● a-ExN+a xN+2 atE
当 n > N 时, 总有 记作 此时也称数列收敛 , 否则称数列发散 . 几何解释 : a − a + ( ) a − x a + n (n N ) 即 x U (a, ) n (n N ) xn a n = → lim 或 x → a (n → ) n N+1 x N+2 x 则称该数列 的极限为 a , 数列极限的 −N 定义

123 n 例如 234 n+1 →1(n→o) n+1 143 n+(-1)n-l 收 2 23’4 n 敛 n+(-011(n→m)J n 2,4,8,.,2”,. xn=2”→0(n→0) 发 1,-1,1,.,(-10m1,. 散 x=(-1)+1f 趋势不定
例如 ,1 , , 43, 32, 21 n +n +1 = nn xn →1 (n →) n n x n n 1 ( 1) − + − = →1 (n →) 2 , 4 , 8 , , 2n , n nx = 2 → (n →) 1 ( 1) + = − n nx 趋势不定 收敛发散

例4设数列xn=C(常数),证明limx=C. n->oo 例5证明 lim n+(-1)-_1 n-→0 2n 2. 例6已知xn= +疗,证明m,=0. (-1)” n->00 例7 证明1imq”=0,其中goo
n x C= lim n n x C → 例4 设数列 (常数),证明 = . 例5 证明 1 ( 1) 1 lim 2 2 n n n n − → + − = . 例6 已知 证明 lim 0 n n q → 例7 证明 = ,其中 q 1

二、函数的极限 (1)自变量趋于无穷大时函数的极限 (2)自变量趋于有限值时函数的极限 1、自变量趋于无穷大时函数的极限 观察函数 sinx y= sinx 当X>00 时的变化趋势
二、函数的极限 (1)自变量趋于无穷大时函数的极限 (2)自变量趋于有限值时函数的极限 1、自变量趋于无穷大时函数的极限 sin x y x = x y o sin x y x = x → 观察函数 当 时的变化趋势

定义2设函数f(x)当x大于某一正数时有定 义,如果存在常数A,对于任意给定的正数E(无 论它有多么的小),总存在正数X,使得适合不等 式x>X的一切x,所对应的函数值f(x)都满足 不等式f(x)-0,彐X>0,使当x>X时,恒有f(x)-A<
定义2 设函数 当 大于某一正数时有定 义,如果存在常数 ,对于任意给定的正数 (无 论它有多么的小),总存在正数 ,使得适合不等 式 的一切 ,所对应的函数值 都满足 不等式 ,那么常数 就叫做函数 当 趋于无穷大时的极限,记做 或 f x( ) x A X x X x f x( ) f x A ( ) − A f x( ) x lim ( ) x f x A → = f (x) → A ( x → )。 = → f x A x lim ( ) − 0, 0, , ( ) X x X f x A 使当 时 恒有 函数的 − X 定义
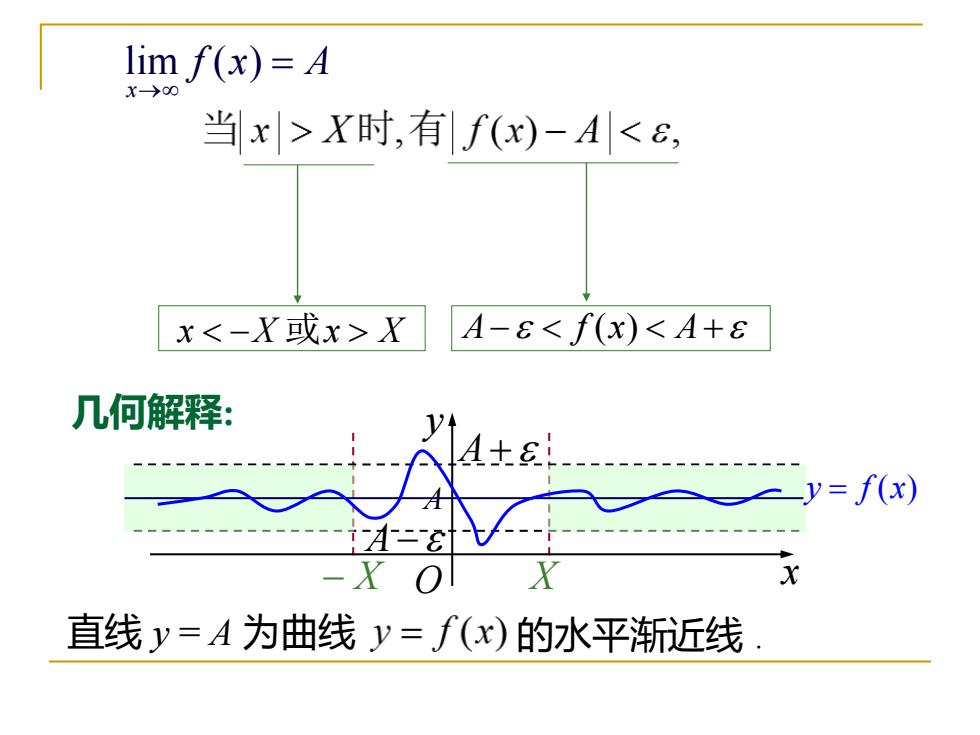
lim f(x)=4 X→00 当x>X时,有f(x)-AX A-8<f(x)<A+8 几何解释: 4-al 三y=f(x) 直线y=A为曲线y=∫(x)的水平渐近线
lim ( ) x f x A → = x −X 或x X A− f (x) A+ − X X A+ A− O x y y f x = ( ) A 几何解释: 直线 y = A 为曲线 的水平渐近线