
§7.3全微分 一元函数的可微性概念复习 一、全微分 定义如果函数z=f(x,y)在点(x,y)的全增量 △z=f(x+△x,y+△y)-f(x,y) 可表示为 △2=AAx+B△y+O(p) 其中A、B与△x、△y无关,仅与、y有关,p=V(Ax)2+(Ay)2 则称函数z=f(x,y)在点(x,y)可微分,A△x+B△y称为 函数z=fx,y)在点(x,y)的全微分,记作d正,即 dz=A△x+B△y
§7.3 全微分 一元函数的可微性概念复习 一、全微分 定义 如果函数 在点 的全增量 可表示为 其中 、 与 、 无关,仅与 、 有关, 则称函数 在点 可微分, 称为 函数 在点 的全微分,记作 ,即 z = f (x, y) (x, y) z = f (x + x, y + y) − f (x, y) z = Ax + By + o() A B x y x y 2 2 = (x) + (y) z = f (x, y) (x, y) Ax + By z = f (x, y) (x, y) dz dz = Ax + By

如果函数z=f(x,y)在区域D内的每一点都可微 分,则称函数z=f(x,y)在区域D内可微。 定理1(可微的必要条件)如果函数z=f(x,y) 在点(x,y)可微分,则函数z=f(x,)在点(x,y)的偏 导数、距 存在,且有 ax dy dz a2+0y 8x yo
如果函数 z = f (x, y) 在区域 D 内的每一点都可微 分,则称函数 z = f (x, y) 在区域 D 内可微。 在点 定理1 (可微的必要条件) 如果函数 可微分,则函数 在点 的偏 y y z x x z z + d = z = f (x, y) (x, y) z = f (x, y) (x, y) x z y z 导数 、 存在,且有

例1讨论函数 x2+y2≠0 x2+y2=0 在点(0,0)的可微性。 定理2(可微的充分条件)如果函数z=f(x,y) 在点(x,y)的某一邻域内存在偏导数) 0z02 ,且这 两个偏导数在点(x,y)连续,则函数2=f(x,y)在点 (x,y)可微
例1 讨论函数 2 2 2 2 2 2 0 ( , ) 0 0 xy x y f x y x y x y + = + + = 在点 (0,0) 的可微性。 定理2 (可微的充分条件) 如果函数 的某一邻域内存在偏导数 、 ,且这 两个偏导数在点 连续,则函数 在点 在点 z = f (x, y) (x, y) x z y z (x, y) z = f (x, y) (x, y) 可微

定理2说明,两个偏导数连续,则函数可微分, 但是,反之则未必成立。 例如 x2+y2=0 在点(0,0)处可微分,但是其两个偏导数在(0,0)处 都不连续
定理2说明,两个偏导数连续,则函数可微分, 但是,反之则未必成立。 例如 2 2 2 2 2 2 2 2 1 ( )sin , 0 ( , ) 0 0 x y x y f x y x y x y + + = + + = 在点 处可微分,但是其两个偏导数在 处 都不连续。 (0,0) (0,0)

例1计算函数z=ey在点(2,1)处的全微分. dz e'dx +2e'dy. 例2求函数z=yc0s(x-2y),当x=,y=兀, =4=元时的全微分。 8(4-7》 例3求函数u=ln(xy+z2)的全微分
例 2 求函数 z = y cos( x − 2 y) ,当 4 p x = ,y = p , 4 p dx = ,dy = p 时的全微分 。 2 (4 7 ) 8 ( p p − ) 例 1 计算函数 x y z = e 在点(2,1) 处的全微分. 2 . 2 2 dz = e dx + e dy 例3 求函数 ln( ) 2 u = x y + z 的全微分

例4 试证函数 f(比,y)= sin+y2,(x,)≠(0,0 在 0, (x,y)=(0,0) 点(0,0)连续且偏导数存在,但偏导数在点(0,0) 不连续,而f在点(0,0)可微。 思路:按有关定义讨论;对于偏导数需分 (x,y)≠(0,0),(x,y)=(0,0)讨论. 证令 x=pcos0, 则 lim xysin- y=psine, (x,y)-→(0,0) vx2+y2
思路:按有关定义讨论;对于偏导数需分 (x, y) (0,0),(x, y) = (0,0)讨论. 证 令 x = cos , y = sin , 则 2 2 ( , ) (0,0) 1 lim sin x y xy x y → + 例 4 试证函数 = = + 0, ( , ) (0,0) , ( , ) (0,0) 1 sin ( , ) 2 2 x y x y x y xy f x y 在 点(0,0)连续且偏导数存在,但偏导数在点(0,0) 不连续,而 f 在点 (0,0) 可微

limp2sinecose.sin=0=f(0,0), 故函数在点(0,0)连续, f(0,0)=lim (,x0)-f0,0) 0-0 △-→0 △x lim =0, Ax-0△x 同理 f(0,0)=0. 当(x,y)≠(0,0)时, 1 x2y f(x,y)=ysin- 当点P(x,y)沿直线y=x趋于(0,0)时
1 lim sin cos sin 2 0 = → = 0 = f (0,0), 故函数在点(0,0)连续, f x (0,0) = x f x f x − → ( ,0) (0,0) lim 0 0, 0 0 lim 0 = − = x→ x 同理 (0,0) = 0. y f f x (x, y) = , 1 cos ( ) 1 sin 2 2 3 2 2 2 2 2 x y x y x y x y y + + − + 当 (x, y) (0,0) 时, 当点 P( x, y)沿直线 y = x趋于 (0,0) 时

lim f (x,y) (x,x)-→(0,0) n2l2irom x3 不存在 所以f(x,y)在(0,0)不连续. 同理可证∫(x,y)在(0,0)不连续 △f=f(△x,△y)-f0,0)=△x·Ay·sin (△x)2+(Ay)1 =o(V(△x)2+(△y)2) 故f(x,y)在点(0,0)可微
lim ( , ) ( , ) (0,0) f x y x x x → , 2 | | 1 cos 2 | | 2 2 | | 1 lim sin 3 3 0 = − → x x x x x x 不存在. 所以 f (x, y) x 在(0,0)不连续. 同理可证 f ( x, y) y 在(0,0)不连续. f = f (x,y) − f (0,0) 2 2 ( ) ( ) 1 sin x y x y + = ( ( ) ( ) ) 2 2 = o x + y 故 f (x, y)在点(0,0)可微
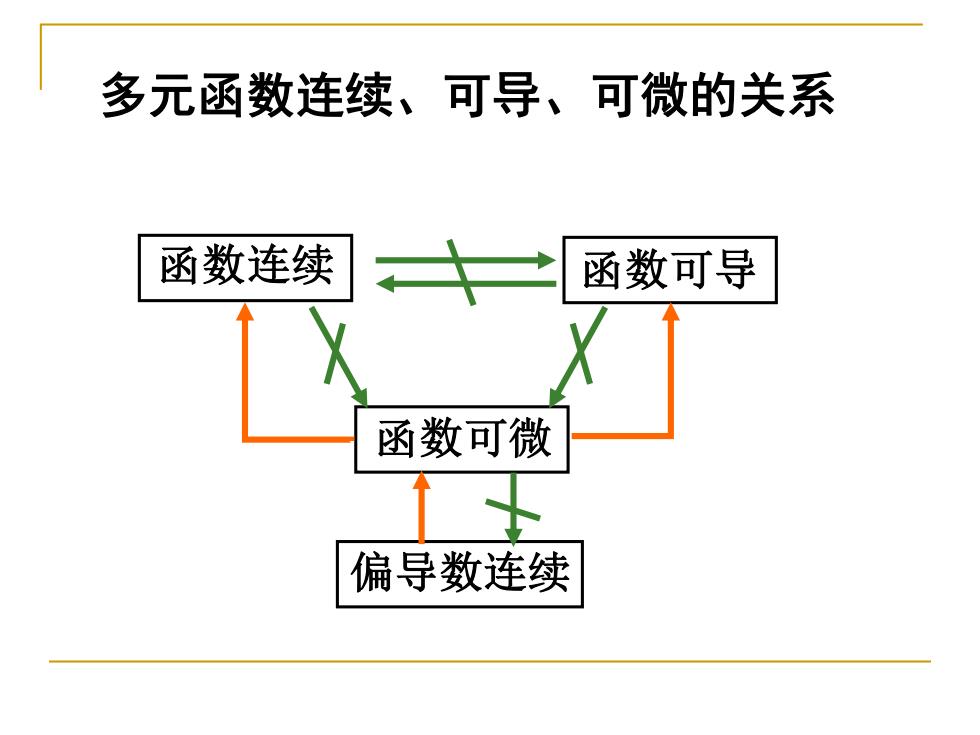
多元函数连续、可导、可微的关系 函数连续 函数可导 函数可微 偏导数连续
多元函数连续、可导、可微的关系 函数可微 函数连续 偏导数连续 函数可导

二、全微分在近似计算中的应用 如果二元函数z=f(x,y)的两个偏导数f(x,y)、 f,(x,y)在点(x,y)连续,并且当△x,|Ay|都较小时, 全增量可近似地用全微分来代替,即 A≈d=f(x,y)△x+f(x,y)Ay 上式也可写为: f(x+△x,y+△y)≈f(x,y)+f(x,y)△x+f(x,y)△ 利用上式可以对二元函数进行近似计算
二、全微分在近似计算中的应用 如果二元函数 的两个偏导数 、 在点 连续,并且当 , 都较小时, 全增量可近似地用全微分来代替,即 上式也可写为: 利用上式可以对二元函数进行近似计算。 z = f (x, y) f (x, y) x f (x, y) y (x, y) | x | | y | z z f x y x f x y y d = x ( , ) + y ( , ) f x x y y f x y f x y x f x y y ( + , + ) ( , ) + x ( , ) + y ( , )