
§1.5函数极限存在准则 两个重要极限 如果数列{xn}满足条件 X1≤X2≤X3≤.≤Xn≤. 则称数列{x}是单调增加的; 如果数列{x}满足条件 X1≥X2≥X3≥.≥Xn≥. 则称数列x}是单调减少的。 单调增加数列和单调减少的数列统称为单调数列
§1.5 函数极限存在准则 两个重要极限 如果数列 xn 满足条件 x1 x2 x3 xn 则称数列 xn 是单调增加的; 如果数列 xn 满足条件 x1 x2 x3 xn 则称数列 xn 是单调减少的。 单调增加数列和单调减少的数列统称为单调数列.

准则I单调有界数列必有极限. 注:(1)利用准则I来判定数列收敛必须同时 满足数列单调和有界这两个条件. (2)单调是数列收敛的充分条件,而非必要条 件. (3)准则I只能判定数列极限的存在,而未给 出求极限的方法
(3)准则Ⅰ只能判定数列极限的存在,而未给 出求极限的方法. 准则Ⅰ 单调有界数列必有极限 . 注:(1)利用准则Ⅰ来判定数列收敛必须同时 满足数列单调和有界这两个条件. (2)单调是数列收敛的充分条件,而非必要条 件.

证明数列 -+ 当n趋于无穷大时收敛. 二项式定理复习: (a+b}”=∑Ca"*b, Ci= n! n(n-1)(n-2).(n-k-1) !(n-k)! k! e=2.718281828459045
1 1 n n x n = + 证明数列 当 n 趋于无穷大时收敛 . 二项式定理复习: ( ) 0 , ! ( 1)( 2) ( 1) !( )! ! n n k n k k n k k n a b C a b n n n n n k C k n k k − = + = − − − − = = − . e 2.718281828459045 =

对于准则I,,函数极限也有类似的准则,自变 量的不同变化过程(x→x0,x→x, X>00’ x→+∞),准则有不同的形式.例如: 准则'设函数f(x)在点,的某个左邻域内单调 并且有界,则f(x)在x的左极限f(x。)必存在 例求 1+3 例2求 lim x→00
的左极限 I f x( ) 0 x f x( ) 0 x 0 f x( ) − 准则 设函数 在点 的某个左邻域内单调 并且有界,则 在 必存在. 对于准则Ⅰ,函数极限也有类似的准则,自变 量的不同变化过程( , , , ),准则有不同的形式.例如: 0 x x → − 0 x x → + x → − x → + 例2 求 1 lim 1 x x x → x + − 例3 求 1 0 lim 1 3 x x x x + → + 例1 求 1 lim 1 x x→ x −

准则Ⅱ如果数列{xn}、y,n}及{2n}满足下列条件: (1)yn≤xn≤2n,n=1,2,3,. (2)lim yn=a,lim =n=a n->oo n-→0o 则数列{xn}的极限存在,且xm=a 2 例4 证明 limsin=0 n 例5求极限 lim n-0
n n n y x z n = 1,2,3, yn a n = → lim zn a n = → lim xn xn a n = → lim 准则 II 如果数列 xn 、 yn 及 zn 满足下列条件: 则数列 的极限存在,且 . (1) (2) , , 例4 证明 2 lim sin 0 n→ n = . 例5 求极限 2 2 2 1 1 1 lim 1 2 n n n n n → + + + + + + .

准则Ⅱ'设函数f(x)在点x的某一去心邻域U(x,) 内(或x≥X)满足条件: (1)g(x)≤f(x)≤h(x) (2) ling()=4,imx)=4 ()=4, →X limh(x)=A). r-o 则limf(x)存在,且limf(x)=A(或Iimf(x)=A 存在,且limf(x))
准则 II f (x) 0 x 0 0 U x( , ) x X 设函数 在点 的某一去心邻域 内(或 )满足条件: 0 lim ( ) x x f x → 0 lim ( ) x x f x A → = lim f (x) x→ f x A x = → 则 (或 lim ( ) 存在,且 存在,且 )。 ( g(x) f (x) h(x) 1) g x A x = → lim ( ) h x A x = → lim ( ) 0 lim ( ) x x g x A → = 0 lim ( ) x x h x A → , = (或 , ). (2)
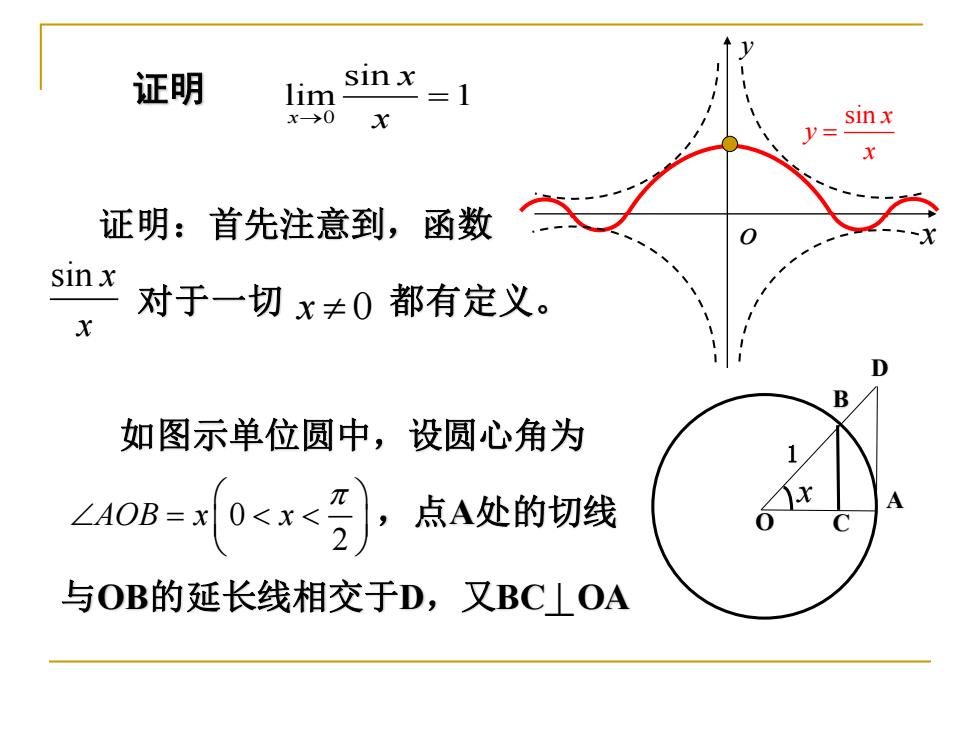
证明 lim sinx 二1 x>0 sinx 证明:首先注意到,函数 sinx 对于一切x≠0都有定义。 如图示单位圆中,设圆心角为 ∠408=0x引点A处的切线 与OB的延长线相交于D,又BCOA
证明 0 sin lim 1 x x → x = 证明:首先注意到,函数 对于一切 都有定义。 sin x x x 0 如图示单位圆中,设圆心角为 ,点A处的切线 与OB的延长线相交于D,又BC OA O 1 A B C D x 0 2 AOB x x = ⊥ o x y sin x y x =

则有: sinx CB,x=AB,tanx=AD 因为: △AOB的面积<圆扇形AOB的面积<△AOD的面积 1 11 D 所以 sinx<。x<-tanx→sinx<x<tanx B 2 22 不等式两边同除以sinx,即得 1<x 1 或 COSx< sinx <1 sinx cosx ,lim cosx=l→limS x→0 四-1,以上对(号亦成立
O 1 A B C D x 则有: sin , ,tan x CB x AB x AD = = = 因为: ∆AOB的面积<圆扇形AOB的面积< ∆AOD的面积 所以 1 1 1 sin tan 2 2 2 x x x sin tan x x x 不等式两边同除以 sin x ,即得 1 1 , sin cos x x x sin cos 1 x x x 或 以上对 , 0 亦成立。 2 x − 0 0 sin lim cos 1 lim 1 x x x x → → x = =

例6求 lim tan x x>0 x sin 3x 例7求极限 lim →0sin5x tan x-sinx 例8求极限 lim x→0 习题:P34EX1-5
0 tan lim x x → x 例6 求 例7 求极限 0 sin 3 lim x sin 5 x → x 例8 求极限 3 0 tan sin lim x x x x − → . 习题:P34 EX 1—5