
第一章 函数与极限 函数是微积分学的研究对象,极限是研究函数的基 本方法。 §1.1函数 一、函数的定义 定义1设两个变量x和y,当变量x在一给定的 数集D中任意取一个值时,变量y按照一定的法则 f总有确定的数值和它对应,则称y是x的函数, 记作y=f(x)·
第一章 函数与极限 函数是微积分学的研究对象,极限是研究函数的基 本方法。 §1.1 函数 一、函数的定义 定义1 设两个变量 和 , 当变量 在一给定的 数集 中任意取一个值时,变量 按照一定的法则 总有确定的数值和它对应,则称 是 的函数, 记作 . f x y x D y y x y f x = ( )

定义域 y=f(x),x∈D 因变量 自变量 Rt=f(D)={yy=f(x),xED) 称为值域 确定函数的两个要素: 1、定义域; 2、对应关系。 Vx∈Df一yeR=f(D)={yy=f(x),x∈D} 定义域)口 (对应规则) (值域)
定义域 y f x x D = ( ), 称为值域 因变量 自变量 Rf = f (D) = y y = f (x), x D x D f y Rf = f (D) = y y = f (x), x D (定义域) (对应规则) (值域) 确定函数的两个要素: 1、定义域; 2、对应关系

两点说明: 定义域 使表达式或实际问题有意义的自变量集合. 对应规律的表示方法解析法、图像法、列表法。 例1讨论下列函数的定义域、值域。 O 1x (1)y=f(x)=arcsinx 2四=-{8
定义域 对应规律的表示方法 解析法、图像法、列表法。 使表达式或实际问题有意义的自变量集合. 两点说明: 例1 讨论下列函数的定义域、值域。 (1) (2) O y 2 − 1 −1 x 2

例2已知函数y=f(x)= 2Vx,0≤x≤1 1+x,x>1 写出函数的定义域及值域,并求f()及f() 此函数为分段定义 y=1+x 函数,非初等函数。 =2元 在经济应用中,变量p 一般表示价格,需求函数通常由Q=Q(p)=1表 示;供给函数通常由S=S(p)表示
例2 已知函数 + = = 1 , 1 2 , 0 1 ( ) x x x x y f x ( ) 2 1 f 及 ( ). 1 t 写出函数的定义域及值域, 并求 f x y O y = 2 x y =1+ x 1 此函数为分段定义 函数,非初等函数。 一般表示价格,需求函数通常由 表 示;供给函数通常由 表示。 p 1 Q Q p( ) p = = 在经济应用中,变量 S S p = ( )

二、函数的几种特性 1、单调性 设函数的定义域为D,区间IcD·如果对于 I上任意两点x及x,当xf(x,)成立,则称函数在区间上 是单调增加(减少)的。 单调增加和单调减少的函数统称为单调函数, 区间称为单调区间. 上述单调又称作严格单调性
二、函数的几种特性 1、单调性 设函数的定义域为 ,区间 .如果对于 上任意两点 及 ,当 时,恒有不等式 成立, 则称函数在区间上 是单调增加(减少)的。 D I D I 1 x 2 x 1 2 x x 1 2 f x f x ( ) ( ) 1 2 ( ( ) ( )) f x f x 上述单调又称作严格单调性。 单调增加和单调减少的函数统称为单调函数, 区间称为单调区间

2、奇偶性 VxeD,且有-x∈D, 若∫(-x)=∫(x),则称f(x)为偶函数 若f(-x)=-f(x),则称f(x)为奇函数 说明:若f(x)在x=0有定义, 则当f(x)为奇函数时, 必有f(0)=0
xD, 且有 − xD, 若 则称 f (x) 为偶函数; 若 则称 f (x) 为奇函数. 说明: 若 f (x) 在 x = 0 有定义 , f (0) = 0. f (x) 为奇函数时, x y 则当 − x O x 必有 2、奇偶性
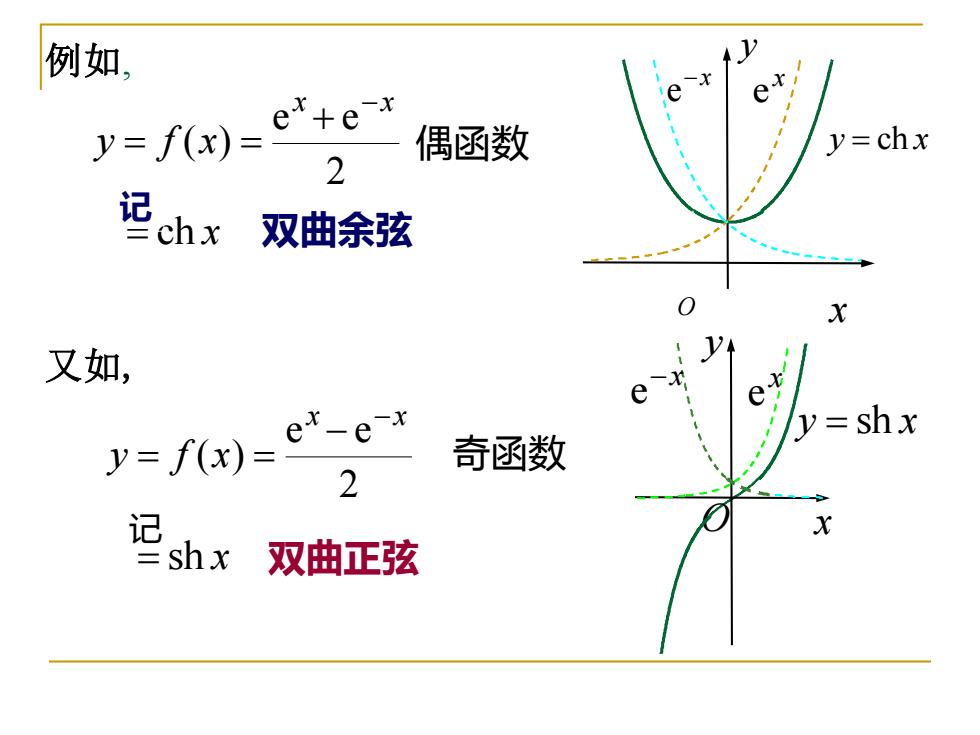
例如, y=f(x)= ex+e-x 偶函数 y=chx 2 chx 双曲余弦 X 又如, y=shx y=f(x)= ex-e-x 奇函数 2 记 X shx 双曲正弦
例如, 2 e e ( ) x x y f x − + = = = ch x 偶函数 x y O x e −x e y = ch x 双曲余弦 记 又如, 奇函数 = sh x 双曲正弦 记 x y O x e −x e y = sh x 2 e e ( ) x x y f x − − = =
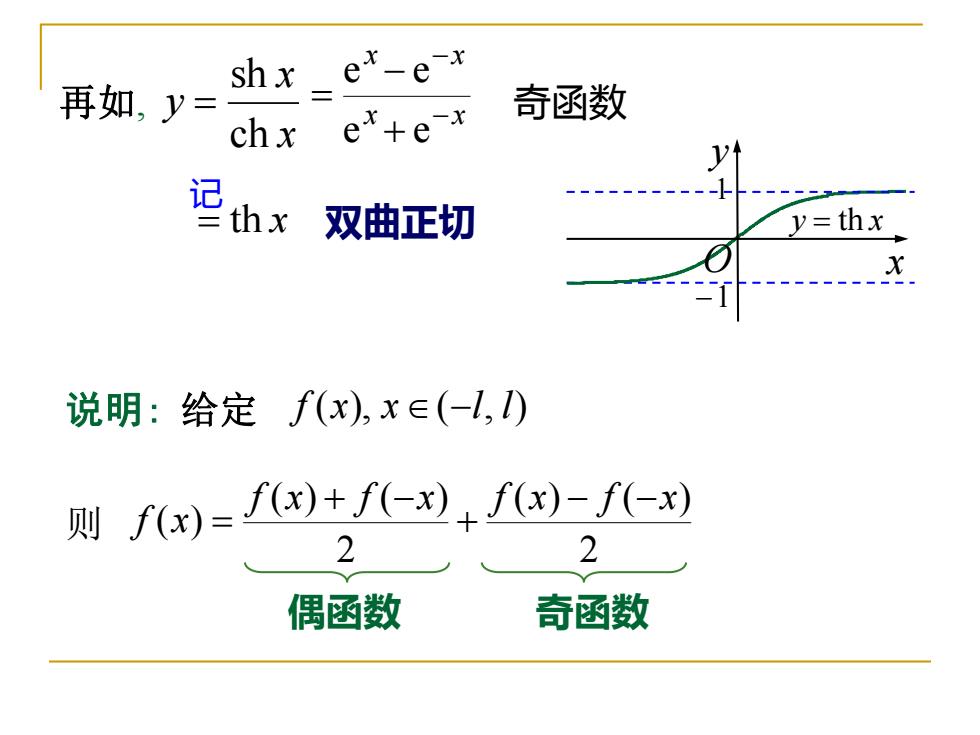
再如,y= shx ex-e-x chx ex+e-x 奇函数 V 记hx 双曲正切 y=thx 说明:给定f(x),x∈(-1,) f(x)=I(x)+f(-x:f(x)-f(-x) 2 2 偶函数 奇函数
再如, x x y ch sh = 奇函数 = th x 双曲正切 记 O y x 1 −1 y = th x x x x x − − + − = e e e e 说明: 给定 f (x), x(−l, l) 则 2 ( ) ( ) 2 ( ) ( ) ( ) f x f x f x f x f x − − + + − = 偶函数 奇函数

3.有界性 设函数f(x)的定义域为D,如果存在数M(L), 使得对每一个x∈D有f(x)≤M(f(x)≥L),则称函 数f(x)在D上有上(下)界,称M(L)为f(x)在D上 的一个上(下)界. 如果存在正数M,使得对每一个x∈D有 f(x≤M 则称函数f(x)在D上有界
如果存在正数 M ,使得对每一个 有 则称函数 在 上有界. x D f x M ( ) f x( ) D 3.有界性 设函数 的定义域为 ,如果存在数 , 使得对每一个 有 ( ),则称函 数 在 上有上(下)界,称 为 在 上 的一个上(下)界. f x( ) D x D f x M ( ) f x L ( ) f x( ) D M L( ) f x( ) D M L( )
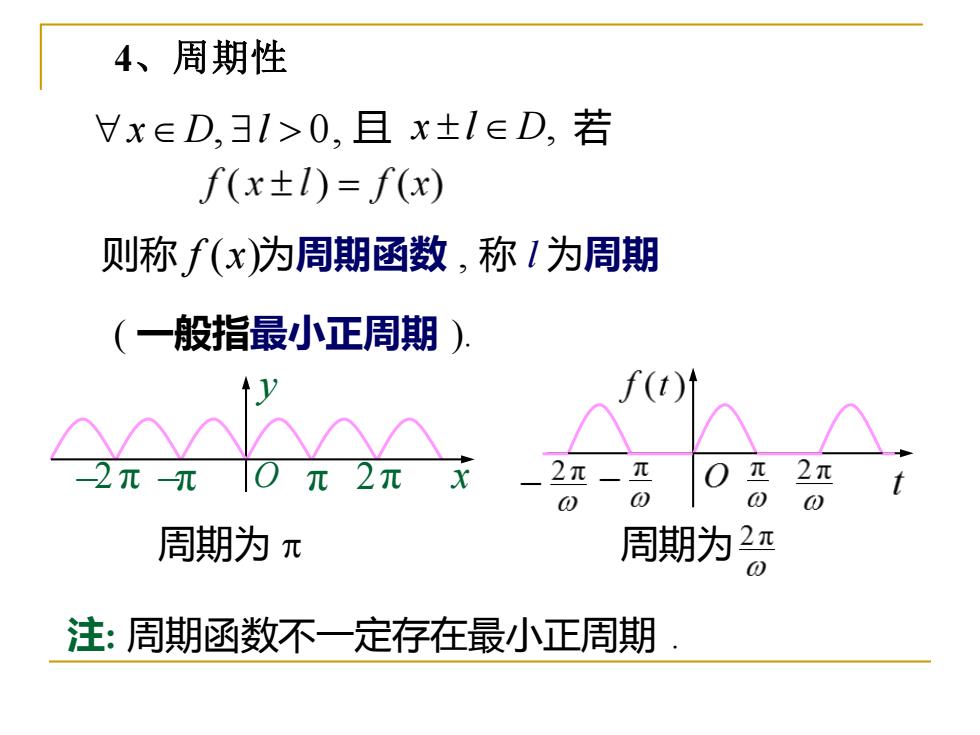
4、周期性 Vx∈D,31>0,且x±I∈D,若 f(x±)=f(x) 则称f(x)为周期函数,称1为周期 (一般指最小正周期) f(t)1 -2元元10元2元方 2π- 2元 0 周期为元 周期为2π 注:周期函数不一定存在最小正周期
xD, l 0, 且 x l D, 则称 f (x) 为周期函数 , 2 π −π O π π x y − 2 若 称 l 为周期 ( 一般指最小正周期 ). 周期为 周期为 注: 周期函数不一定存在最小正周期 . 4、周期性