
上次课内容复习: 定积分的几何应用 1.平面图形的面积 直角坐标方程 边界方程 参数方程A=w()p')d1 极坐标方程4=0(0d0 2.已知平行截面面面积函数的立体体积 V=∫84Ax)dx
上次课内容复习: 定积分的几何应用 1. 平面图形的面积 边界方程 参数方程 极坐标方程 直角坐标方程 2. 已知平行截面面面积函数的立体体积
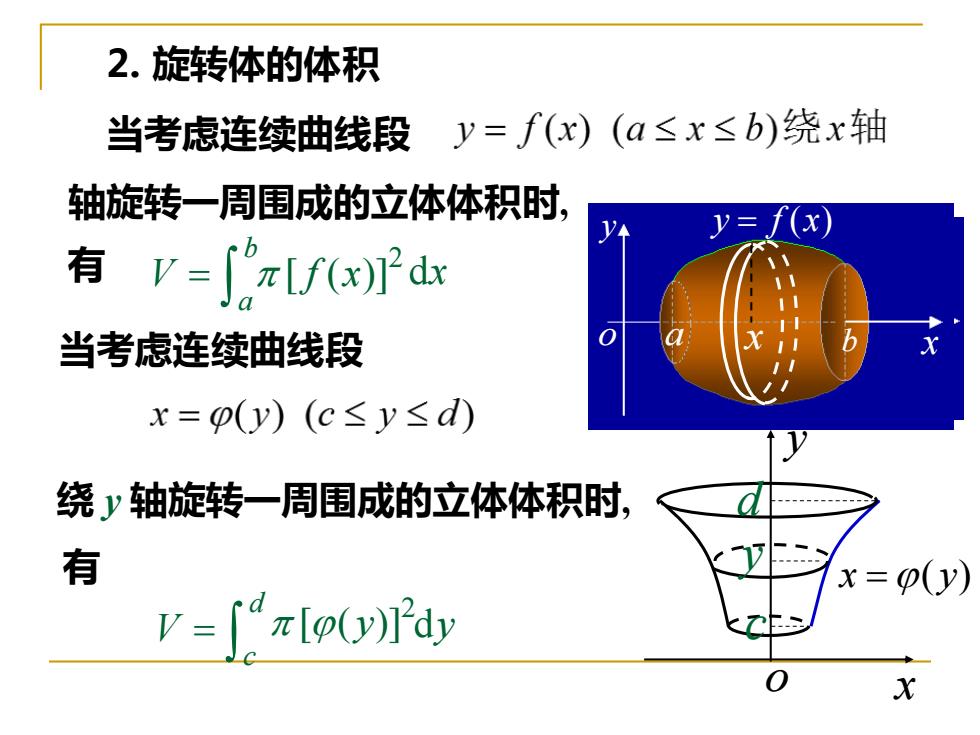
2.旋转体的体积 当考虑连续曲线段y=f(x)(a≤x≤b)绕x轴 轴旋转一周围成的立体体积时, y= 有v=∫x[fx]d 当考虑连续曲线段 x=p(y)(c≤y≤d) 绕y轴旋转一周围成的立体体积时, 有 =(y) V=π[p(y)2dy X
x y o a b x y o a b y f x = ( ) 当考虑连续曲线段 2 [ f (x)] 轴旋转一周围成的立体体积时, 有 dx = b a V 当考虑连续曲线段 绕 y 轴旋转一周围成的立体体积时, 有 2 [( y)] dy = d c V x o x y x =( y) c d y 2. 旋转体的体积

例8计算由椭圆 xB? 62 =1所围图形绕x轴旋转而 转而成的椭球体的体积 解:方法1利用直角坐标方程 y=ba2-2(a≤xsj 则 利用对称性) -2rJ(a2-x)dx b =2π2 4 πab2
a y x b 例8 计算由椭圆 所围图形绕 x 轴旋转而 转而成的椭球体的体积. 解: 方法1 利用直角坐标方程 则 a x x a b a 2 ( )d 2 0 2 2 2 = − (利用对称性) = − 2 3 2 2 3 1 2 a x x a b 0 a 2 3 4 = ab o = a V 0 2 y dx 2 x

方法2利用椭圆参数方程 x=acost y=bsint 则V=2ry2d=2xj0abs =2xab2.2.1 4 4 特别当b=a时,就得半径为a的球体的体积πa3
方法2 利用椭圆参数方程 则 V y x a 2 d 0 2 = 2 ab sin t dt 2 3 = 2 = 2 ab 3 2 2 3 4 = ab 1 特别当b = a 时, 就得半径为a 的球体的体积 . 3 4 3 a
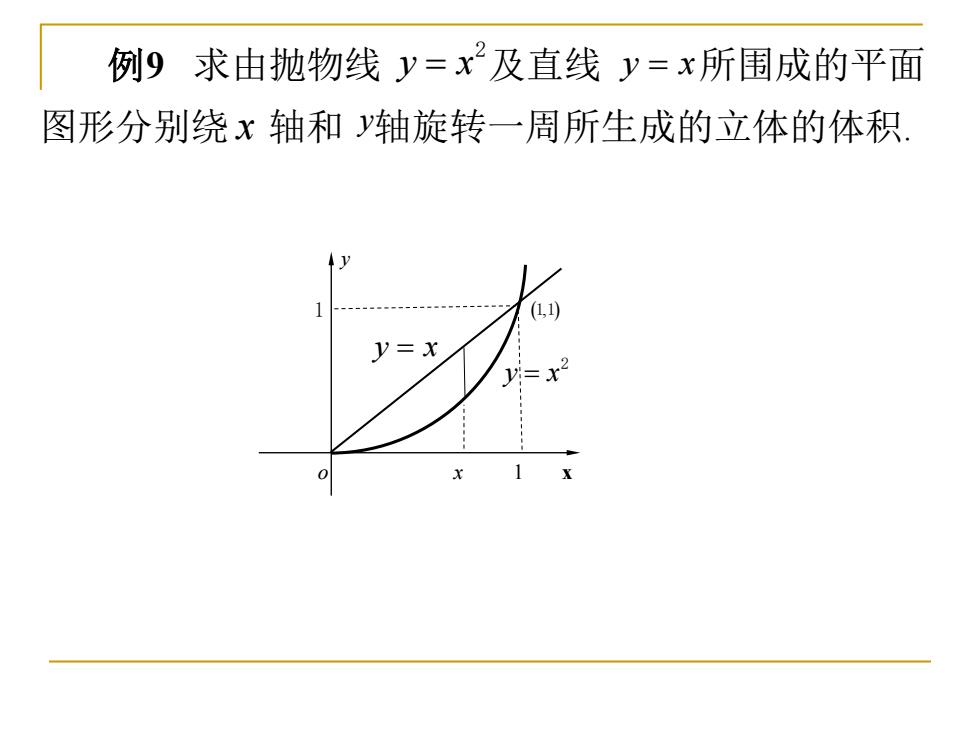
例9求由抛物线y=x及直线y=x所围成的平面 图形分别绕x轴和y轴旋转一周所生成的立体的体积 (1,10 y=x
图形分别绕 轴和 轴旋转一周所生成的立体的体积. 例9 求由抛物线 y x = 及直线 所围成的平面 2 y x = x y y x = 2 y y x = 1 (11, ) o x 1 x

定积分及其应用习题课 习题中的问题 P135EX5-12利用定积分的几何意义写出下列定积分的值。 (1)∫a2-dr= (2) 3.比较下列积分值的大小(用等号或不等号表示) (3)∫Inx)dx∫dnx)d (4)∫。ed :∫I+x) 5.应用估值定理证明: :2es∫店e"dx s2
定积分及其应用习题课 习题中的问题 P135 EX5-1 2 利用定积分的几何意义写出下列定积分的值。 (1) 2 2 0 d a a x x − = (2) π 2 π 2 sin dx x − = 3. 比较下列积分值的大小(用等号或不等号表示) e 2 1 (ln ) d x x e 3 1 (ln ) d x x 1 0 e dx x 1 0 (1 )d + x x (3) (4) 2 1 2 e − 2 1 2 1 2 e d x x − − 5.应用估值定理证明: 2

6.设函数f( [0,1]上连续,在(0,1)内可导,且 3f2f(x)dx=f(0) 证明:在(0,内至少存在一点使f'(c)=0
f x( ) [0,1] (0,1) 1 2 3 3 ( )d (0) f x x f = (0,1) c f c'( ) 0 = 6.设函数 在 证明:在 内至少存在一点 使 . 上连续,在 内可导,且

1.填空题 (1)设f(x)在[a,证连续, a≤x≤b (2) _dt (3) (4) tantdt lim 0 x→0 x2
f x( ) [ , ] a b a x b d ( )d d x a f t t x = d ( )d d b x f t t x = 2 0 d sin d d 1 cos x t t t x t = + sin 2 0 d 1 d d x t t t x + = 0 2 0 tan d lim x x t t → x = 1.填空题 (1) 设 上连续, , ; . . . . 在 (2) (3) (4)

2设f(x)=∫,mdt,g(x)=x+r,则当x→0时, f(x)是g(x)的() (A)等价无穷小;(B)同阶但非等价无穷小; (C高阶无穷小;(D)低阶无穷小. 3.求由∫。edt+∫sindt=0所决定的隐函数y对x 的导数
2 设 ( ) sin 2 3 4 0 ( ) d , ( ) , 0 , ( ) ( ) x f x t t g x x x x f x g x = = + → 则当 时 是 的 (A)等价无穷小;(B) 同阶但非等价无穷小; (C) 高阶无穷小;(D) 低阶无穷小. 0 0 e d sin d 0 y x t t t t + = y x d d y x 3. 求由 所决定的隐函数 对 的导数

设 (t)dr F(x)= X ,x≠0 ,x=0 其中f(x)连续,且f(O)=1试确定G使F(x)在 x=处连续. 5.设F(x)=小ed 试求: (1)F(x)的极值; (2)曲线y=F(拐点的横坐标
0 2 ( )d , 0 ( ) , 0 x tf t t F x x x c x = = f (x ) f (0) 1 = c F x( ) x = 0 设 其中 ,试确定 ,使 处连续. 连续,且 在 F x( ) 2 0 e d x t t − F x( ) y F x = ( ) 5.设 拐点的横坐标. = 试求: (1) 的极值; (2) 曲线