
上次课内容复习: 1、函数的极值及其求法 2、最大值与最小值问题 本次课内容: 1、第六节边际分析与弹性分析 2、第三章习题课
上次课内容复习: 2、最大值与最小值问题 1、函数的极值及其求法 本次课内容: 1、第六节 边际分析与弹性分析 2、第三章习题课

§3.6边际分析与弹性分析 定义1在经济管理中,经济函数f(x)的导数f'(x) 称为边际函数。 据此定义,可以定义边际成本、边际收益、边 际利润、边际需求等函数。 设y=f(x)是一个经济函数,且可导的.当|△x 很小时,△y=f(x+△x)-f(x)=f'(x)△x+o(△x)≈f'(x)△x 特别地,当△x=1或△x=-1时,分别有 Ay=f(x+1)-f(x)≈'(x)或Ay=f(x)-f(x-1)≈f'(x》
§3.6 边际分析与弹性分析 定义1 在经济管理中,经济函数 的导数 称为边际函数。 f x( ) f x ( ) 据此定义,可以定义边际成本、边际收益、边 际利润、边际需求等函数。 y f x = ( ) | | x 0 0 0 0 = + − = + y f x x f x f x x o x f x x ( ) ( ) ( ) ( ) ( ) =x 1 = − x 1 0 0 0 = + − y f x f x f x ( 1) ( ) ( ) 0 0 0 = − − y f x f x f x ( ) ( 1) ( ) 设 是一个经济函数,且可导的. 当 特别地,当 或 很小时, 时,分别有 或

例1己知某商品的成本函数为 y=C(x)=21+2x3 x为产量,求当x=30时的平均成本、边际成本
3 y C x x = = + ( ) 21 2 x x = 30 例1 已知某商品的成本函数为 为产量,求当 时的平均成本、边际成本

定义2设函数y=f(x)可导,函数的相对改变量 Ay =△x+x)-f)与自变量的相对改变量△r之 y f(x) 比y/, 称为函数f(x)从x到x+△x两点间的相对 △x/x 变化率(或弹性),若当Ax→0时,极限1imAy/心 Ar→0△x/x 存在,则称此极限为函数f(x)在x处的相对变化率 或弹性,记为n,即 lim △y/y=lim Ay.%=y.x Ar→0△x/xAr→0△xy y
定义2 设函数 可导,函数的相对改变量 与自变量的相对改变量 之 比 ,称为函数 从 到 两点间的相对 变化率(或弹性),若当 时,极限 存在,则称此极限为函数 在 处的相对变化率 或弹性,记为 ,即 y f x = ( ) ( ) ( ) ( ) y f x x f x y f x + − = x x y y x x f x( ) x x x + →x 0 0 lim x y y → x x f x( ) x 0 0 lim lim x x y y y x x y x x x y y → → = = =

称刀=y,X为函数f(x的弹性函数,常记为 Ex 当x=x时,称n儿=)高 为f(x)在x=x处 的弹性。 定义3设需求函数Q=Q(p)可导,则称 △Q/Q △p/Po 为需求函数从P到P,+△p两点间的需求弹性,称 -0m)aa 为需求函数在P处的需求弹性,记为
称 为函数 的弹性函数,常记为 , 当 时,称 为 在 处 的弹性。 x y y = f x( ) Ey Ex 0 x x = 0 0 0 0 | ( ) ( ) x x x f x f x = = f x( ) 0 x x = 处的需求弹性,记为 Q Q p = ( ) 0 0 Q Q p p − 0 p 0 p p + 0 0 0 ( ) ( ) p Q p Q p − 0 p d 定义3 设需求函数 两点间的需求弹性,称 为需求函数在 可导,则称 为需求函数从 到

定义4设供给函数Q=S(p)可导,则称 AS/So △pPo 为供给函数从p,到p+△p两点间的供给弹性,称 S为债给函数在处的侠给弹佐,记为% 例2设某商品需求量对价格的函数关系为 0=Qp)=80(31 试求需求量Q对价格p的弹性,并说明其经济意义
Q S p = ( ) 0 0 S S p p 0 p 0 p p + 0 0 0 ( ) ( ) p S p S p 0 p s 定义4 设供给函数 可导,则称 两点间的供给弹性,称 为供给函数在 为供给函数从 到 处的供给弹性,记为 . 1 ( ) 800( ) 3 p Q Q p = = 试求需求量 Q 对价格 p 的弹性,并说明其经济意义. 例2 设某商品需求量对价格的函数关系为
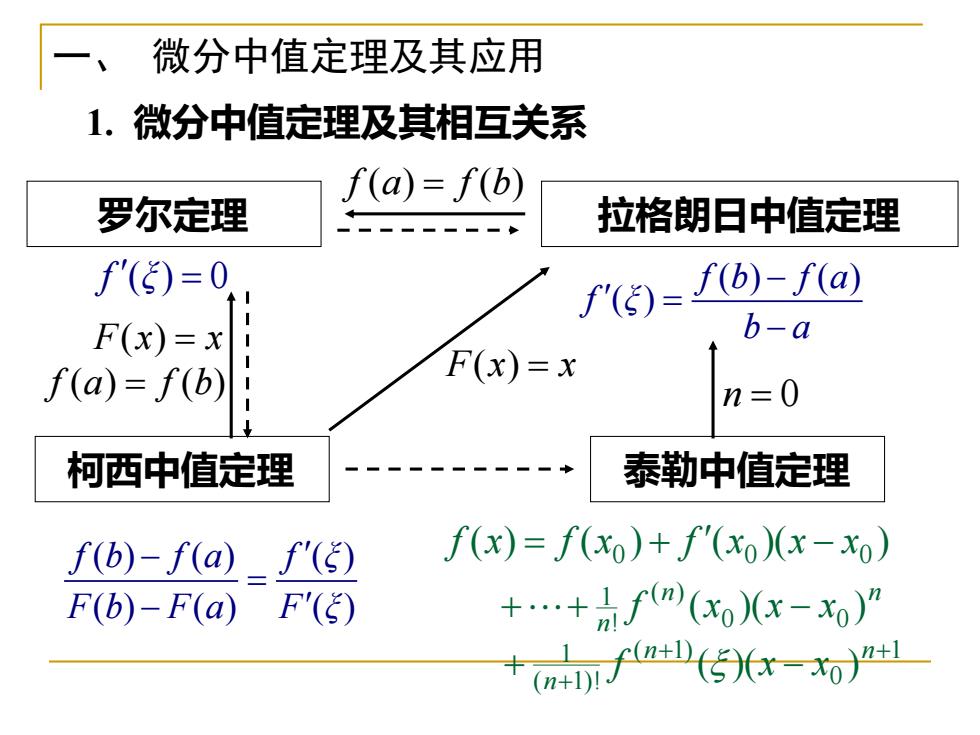
一、微分中值定理及其应用 1.微分中值定理及其相互关系 f(a)=f(b) 罗尔定理 拉格朗日中值定理 f'()=0 M(G)-I(b)-M(a) F(x)=x b-a f(a)=f(b) F(x)=x n=0 柯西中值定理 泰勒中值定理 f(b)-f(a_f'() f(x)=f(xo)+f(xo)(x-x0) F(b)-F(a)F +.+m(x)x-xo)” m子传-o》u
x y O a b y = f (x) 拉格朗日中值定理 f (a) = f (b) 一、 微分中值定理及其应用 1. 微分中值定理及其相互关系 罗尔定理 f ( ) 0 ξ = x y O a b y = f (x) ( ) ( ) ( ) ( ) ( ) ( ) f b f a f ξ F b F a F ξ − = − ( ) ( ) ( ) f b f a f ξ b a − = − 1 0 ( 1) ( 1)! 1 ( )( ) + + + + − n n n f x x F(x) = x 泰勒中值定理 ( ) ( ) ( )( ) 0 0 0 f x = f x + f x x − x n n n f (x )(x x ) 0 0 ( ) ! 1 ++ − n = 0 ( ) ( ) ( ) f a f b F x x = = 柯西中值定理

2.微分中值定理的主要应用 (1)研究函数或导数的性态 (2)证明恒等式或不等式 (3)证明有关中值问题的结论
2. 微分中值定理的主要应用 (1) 研究函数或导数的性态 (2) 证明恒等式或不等式 (3) 证明有关中值问题的结论

3.有关中值问题的解题方法 利用逆向思维,设辅助函数.一般解题方法: (1)证明含一个中值的等式或根的存在,多用罗尔定理, 可用原函数法找辅助函数· (2)若结论中涉及含中值的两个不同函数,可考虑用柯 西中值定理. (3)若结论中含两个或两个以上的中值,必须多次应用 中值定理. (4)若结论为不等式,要注意适当放大或缩小的技巧
3. 有关中值问题的解题方法 利用逆向思维 , 设辅助函数 . 一般解题方法: (1)证明含一个中值的等式或根的存在 , (2) 若结论中涉及含中值的两个不同函数 , (3) 若结论中含两个或两个以上的中值 , 可用原函数法找辅助函数 . 多用罗尔定理, 可考虑用柯 西中值定理 . 必须多次应用 中值定理 . (4) 若结论为不等式 , 要注意适当放大或缩小的技巧

例1.设函数f(x)在(a,b)内可导,且f'(x)≤M, 证明f(x)在(a,b)内有界. 证:取点x0∈(a,b),再取异于x0的点xe(a,b),对 ∫(x)在以o,x为端点的区间上用拉氏中值定理,得 f(x)-f(xo)=f'(5)x-x)(5界于x与x之间) f(x)=f(xo)+f()(x-x) ≤f(xo)+f'(5)x-xo ≤f(xo)+M(b-a)=K (定数) 可见对任意x∈(a,b),f(x)≤K,即得所证
例1. 设函数 在 内可导, 且 证明 在 内有界. 证: 取点 ( , ), x0 a b 再取异于 0 x 的点 x(a,b), 对 为端点的区间上用拉氏中值定理, 得 ( ) ( ) ( )( ) 0 0 f x − f x = f x − x ( ) ( ) ( )( ) 0 0 f x = f x + f x − x 0 0 f (x ) + f ( ) x − x ( ) ( ) f x0 + M b − a = K (定数) 可见对任意 x(a,b), f (x) K , 即得所证