
习题课 不定积分的计算方法 一、求不定积分的基本方法 二、几种特殊类型的积分 课后作业:综合练习四
习题课 一、 求不定积分的基本方法 不定积分的计算方法 二、几种特殊类型的积分 课后作业:综合练习四

一、黄 求不定积分的基本方法 1.直接积分法 通过简单变形,利用基本积分公式和运算法则 求不定积分的方法. 2.换元积分法 ∫f(x)dx 第一类换元法 ∫f[pt]o'(t)d 第二类换元法 (代换:x=p(t) (注意常见的换元积分类型)
一、求不定积分的基本方法 1. 直接积分法 通过简单变形, 利用基本积分公式和运算法则 求不定积分的方法 . 2. 换元积分法 第一类换元法 第二类换元法 (注意常见的换元积分类型) (代换: ) x =(t)

3.分部积分法 Juv dx=uv-∫rdr 使用原则: 1)由v'易求出v; 2)∫uvdx比∫uvdr好球. 一般经验:按“反,对,幂,指,三”的顺 序, 排前者取为u,排后者取为v
3. 分部积分法 = − u v dx u v 使用原则: 1) 由 v 易求出 v ; 2) u v dx 比 好求 . 一般经验: 按“反, 对, 幂, 指 , 三” 的顺 序, 排前者取为 u , 排后者取为 v . u vdx

例1.求 23dx. dax =a*Inadx 器 arctan(号) +C In2-In3
例1. 求 解: 原式 x x x x x d 3 2 2 3 2 2 + = x x x d 1 ( ) ( ) 2 3 2 3 2 + = + = x x 2 3 2 3 2 3 2 1 ( ) d ( ) ln 1 a a a x x x d = ln d C x + − = ln 2 ln3 arctan( ) 3 2

求∫nx+1+2)+5dr. V1+x2 解 原式=j[In(x+1+x)+5]d[ln(x+1+x2)+5] 3[nx+1+7)+5]+C 分析: 2x dx d[ln(x+V1+x2)+5]= 3/)dx x+v1+x2 V1+x2
例2. 求 解: = + + + 2 1 [ln( 1 ) 5] 2 原式 x x d [ln( 1 ) 5] 2 x + + x + 2 x + 1+ x = x x x (1 )d 2 2 1 2 + + 2 1 d x x + = 3 2 = ln( 1 ) 5 2 x + + x + 2 +C 3 分析: d [ln( 1 ) 5] 2 x + + x +
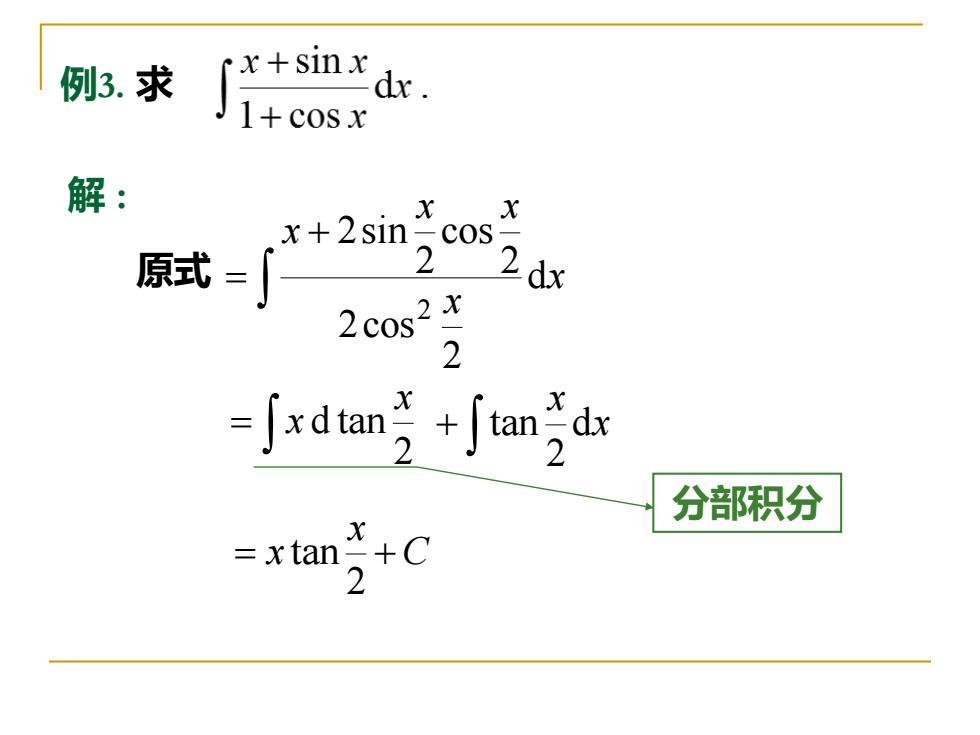
例3.求 解: xx x+2sin cos 原式=∫。 02dx L 2cos 2 分部积分 -+C
例3. 求 解 : 原式 x x x x x d 2 2cos 2 cos 2 2sin 2 + = = 2 d tan x x x x d 2 tan + C x = x + 2 tan 分部积分

例4.求 arctaned ex 解:原式=∫arctane'de -gae-jp‘2 -aan+f+ee产tr 1+e2x =-e*arctane*+x-In(1+e2x)+C
例4. 求 解: = − x 原式 arctan e x e − d x x e arctan e − = − − + x e x e e x x d 1 2 + x x e arctan e − = − x e e e x x x d 1 (1 ) 2 2 2 + + − + x x e arctan e − = − + x e C x − ln(1+ ) + 2 2 1

刚s.求1n=「+a dx 分部积分法对应题型 -2nx 解令w+am-1则 (x2+a2)+,v=x +a )dr X +2nln-2ndl 得递推公式In+1= 1 2na2 (x2+a2ym 2n-In 2na
例5. 求 解: 令 , ( ) 1 2 2 n x a u + = v =1, 则 , ( ) 2 2 2 +1 + − = n x a nx u v = x n I x x a x n n d ( ) 2 2 2 1 2 + + + n x a x ( ) 2 2 + = x x a n n d ( ) 2 2 2 +1 + + n x a x ( ) 2 2 + = n + 2n I 1 2 − 2 n+ na I 得递推公式 n n n I na n x a x na I 1 2 2 2 2 2 2 1 2 ( ) 1 − + + + = 2 2 2 (x + a ) − a n x a x ( ) 2 2 + = 分部积分法对应题型

例6.设F(x)为f(x)的原函数,且F(O)=1,当x≥0时 有f(x)F(x)=sin22x,F(x)≥0,求f(x). 解:由题设F'(x)=f(x),则F(x)F'(x)=sin22x, 故jr四ra=jsm2dr-j小空 即 F2(x)=x-isin4x+C F(0)=1,.C=F2(0)=1,又F(x)≥0,因此 F(x)=x-sin4x+1 故f()=F'()= sin22x /x-isin 4x+1
例6. 设 解: 为 的原函数, 且 求 由题设 F(x) = f (x), 则 故 即 , 因此 故 又

例7.求1=∫ earctanx dx.先换元后分部 解:令t=arctanx,即x=tant,则 1-,ca-j小e'sd, =e'sint-∫e'sintdt V1+ =e'sint+e'cost-Je'cosidt 故I=(sint+cost))e'+C arctan x+C
例7. 求 d . I x = 2 3 (1 ) 2 + x 先换元后分部 令 t = arctan x, 即 x = tant, 则 = t e I t 3 sec sec t d t 2 e t t t cos d = = e t − t sin e t t t sin d e t t = sin e t t t cos d e t − t + cos 故 I t t e C t = (sin + cos ) + 2 1 = 2 1 x e arctan t x 1 2 1+ x 2 1 x x + 2 1 1 + x + e C x + arctan 解: