
上次课内容复习: 1、数列极限£一N的定义 limx=a台 n-→o0 寸6>0,正数N,当n>N时,总有xn-a00 Vε>0,X>0,使当x>X时,恒有f(x)-A<8
上次课内容复习: 当 n > N 时, 总有 lim n n x a → = 2、函数极限的定义 = → f x A x lim ( ) − 0, 0, , ( ) X x X f x A 使当 时 恒有 函数极限的 − X 定义 1、数列极限 −N 的定义

2、自变量趋于有限值时函数的极限 引例.测量正方形面积.(真值:边长为x,;面积为A) 直接观测值 确定直接观测值精度δ: 边长x x-x<δ A Xo 间接观测值 任给精度e,要求x2-A<8 面积x2
2、自变量趋于有限值时函数的极限 引例. 测量正方形面积. (真值: 边长为 面积为A ) 边长 面积 直接观测值 间接观测值 任给精度 , 要求 x − A 2 确定直接观测值精度 : x − x0 0 A x

定义3设函数f(x)在点x,的某一去心邻域内有 定义,如果存在常数A,对于任意给定的正数ε(不 论它多么小),总存在正数δ,使得对于适合不等式 00,36>0, x-→X0 B-δ定义 当0<x-x<6时,有f(x)-A<8
定义3 设函数 在点 的某一去心邻域内有 定义,如果存在常数 , 对于任意给定的正数 (不 论它多么小),总存在正数 ,使得对于适合不等式 的一切 ,对应的函数值 都满足不等 式 ,那么常数 就叫函数 当 趋于 时的极限,记作 或 f (x) 0 x A 0 x − x0 x f (x) f (x) − A A f (x) x 0 x 0 lim ( ) x x f x A → = 0 f x A x x ( ) ( ) → → 当 。 当 时, 有 函数极限的 − 定义 0 0 − x x
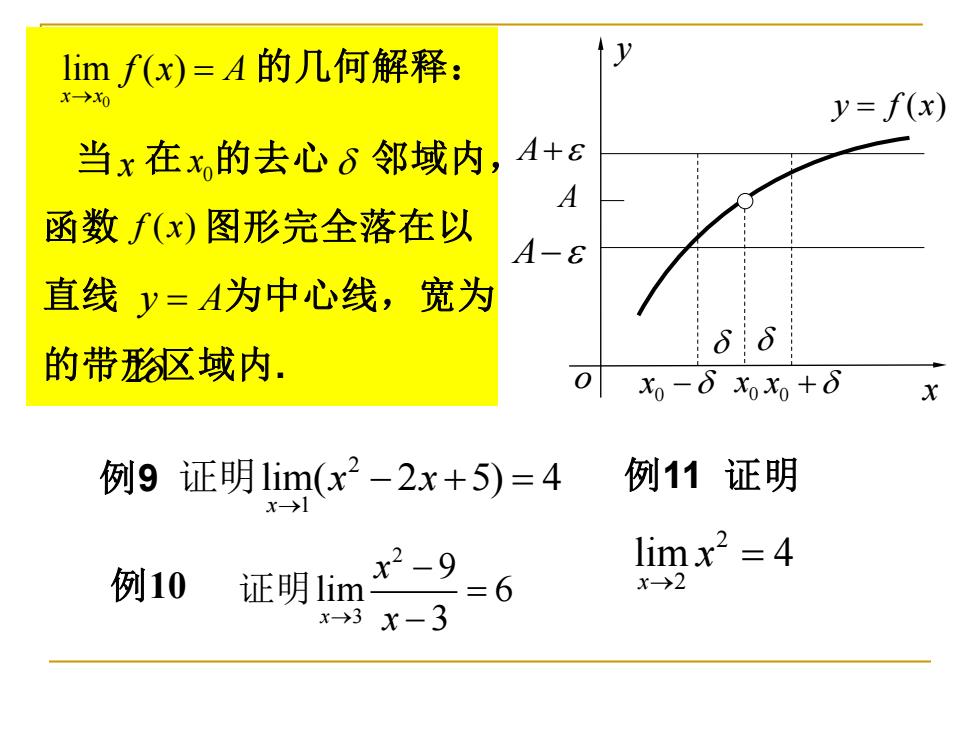
limf(x)=A的几何解释: y y=f(x) 当x在x的去心δ邻域内,A+8 A 函数f(x)图形完全落在以 A- 直线y=A为中心线,宽为 的带形珍区域内. 0 x0-δx0x,+δ X 例9证明1im(x2-2x+5)=4 例11证明 x->I 例10 证明li x2-9 6 limx2 =4 x-→2 x→3X-3
y f x = ( ) y x o A A+ A− 0 x 0 x − 0 x + 的几何解释: 当 在 的去心 邻域内, 函数 图形完全落在以 直线 为中心线,宽为 的带形区域内. 0 lim ( ) x x f x A → = f (x) x 0 x y A = 2 例9 2 1 lim( 2 5) 4 x x x → 证明 − + = 例10 2 3 9 lim 6 x 3 x → x − = − 证明 例11 证明 2 2 lim 4 x x → =

例12证明:当xo>0时1im√x=√xo. x→X0 证1n小-正1-x x-X0 VE>0,欲使f(x)-A<6,只要x-x<Vx6,且 x≥0.而x≥0可用x-x0≤x0保证.故取 6=min{Wxs,xo},则当0<x-xo<6时,必有 x-√x<8 因此 lim√x=Vxo x Xo X→x0
例12 证明: 当 证: 0 0 1 x x x − 0, 欲使 且 而 可用 因此 只要 0 0 lim x x x x = → 时 故取 min , , 0 0 = x x 则当 0 x − x0 时, 保证 . 必有 O x 0 x x

左极限与右极限 左极限f(x-0)=limf(x)=A x→x0 =Ve>0,36>0,当x∈(x-6,x) 时,有f(x)-A0,36>0,当x∈(xo,x0+δ) 定理 时,有f(x)-AX0 x→X0 x→x0
左极限与右极限 左极限 0 f x( 0) − = f x A x x = → − lim ( ) 0 0, 0, 当 ( , ) 0 0 x x − x 时, 有 右极限 0 f x( 0) + = f x A x x = → + lim ( ) 0 0, 0, 当 ( , ) x x0 x0 + 时, 有 定理 f x A x x = → lim ( ) 0 f x f x A x x x x = = → + → − lim ( ) lim ( ) 0 0

1-x,x<0 例13 设f(x)= x2+1,x≥0 证明: lim f(x)=1 x-→0 例14 验证m☒不存在 x→0X 三种极限小结: 1.数列极限 2.函数极限 lim x=a lim f(x)=A lim f(x)=A n→0 x→00 x→x0
2 1 , 0 ( ) 1, 0 x x f x x x − = + 设 0 lim ( ) 1 x f x → = 例13 证明: . 例14 0 lim x x → x 验证 不存在 . 三种极限小结: 1. 数列极限 2. 函数极限 lim n n x a → = lim ( ) x f x A → = 0 lim ( ) x x f x A → =

§1.3极限的运算法则与性质 一、数列极限的性质 定理2(唯一性)若数列{x}收敛,则其极限是 唯一的. 定理3(有界性)若数列{xn}收敛,则数列{xn} 有界 推论无界数列必定发散
一、数列极限的性质 定理2(唯一性)若数列 收敛,则其极限是 唯一的. xn 定理3(有界性)若数列 收敛,则数列 有界 xn xn 推论 无界数列必定发散. §1.3 极限的运算法则与性质

定理4(保号性)如果1imxn=a且a>0 n->oo (或aN时,都 有xn>0(或xn<0). 二、数列极限的四则运算法则 定理1若数列{x}{y}都收敛,设imxn=a lim y.=b则 (1)lim(xn±yn)=limx±limy=a±b
定理1 若数列 都收敛,设 则 (1) . x y n n , xn a n = → lim yn b n = → lim lim( ) lim lim n n n n x x x x y x y a b → → → = = 二、数列极限的四则运算法则 定理4(保号性)如果 且 (或 ),那么存在正整数 N ,当 时,都 有 (或 ). lim n n x a → = a 0 a 0 n N 0 n x 0 n x

(2)lim(xnyn)=limx,limy,=ab,特别地, X00 X>0 lim(Cx,)=C-lim=Ca(为常数):im(x,)=(imx,)=a (3) m- (limy≠0) x→y lim y b'x→∞ X-→00 (4)Im=mx,=a,k为偶数时,要 求limx=a≥0 求数列x:= n2+1 例1 3n2+2n-5 EX:P171-2 当n趋于无穷大时的极限
lim lim (lim 0) lim n n x n x x n n x x x a y y y b → → → → = = lim lim k k k n n x x x x a → → = = k lim 0 n x x a → = (3) . (4) , 为偶数时,要 求 . 2 2 1 3 2 5 n n x n n + = + − 例1 求数列 当 n 趋于无穷大时的极限. (2) ,特别地, (为常数); lim( ) lim lim n n n n x x x x y x y ab → → → = = lim( ) lim n n x x C x C x Ca → → = = lim( ) (lim ) k k k n n x x x x a → → = = EX: P17 1-2