
二重积分部分习题课 ■化二重积分为二次积分的步骤 ■(1)画出积分区域草图; ·(2)选择适当的坐标系; (3)确定积分次序并定出积分限; ■(4)计算二次积分。 ■坐标系的选择方法 (1)两个因素:积分区域的形状与被积函数: (2)若积分区域为圆形、扇形、圆环等,被积函 数呈fx2+,f ,常选择极坐标
二重积分部分习题课 ◼ 化二重积分为二次积分的步骤 ◼ (1)画出积分区域草图; ◼ (2)选择适当的坐标系; ◼ (3)确定积分次序并定出积分限; ◼ (4)计算二次积分。 ◼ 坐标系的选择方法 ◼ (1)两个因素:积分区域的形状与被积函数; ◼ (2)若积分区域为圆形、扇形、圆环等,被积函 数呈 f x y f ( ), 2 2 y ,常选择极坐标。 x +

■积分次序的选择 (1)可积分; ·(2)少分片: ·(3)计算简单。 ■积分限的选择 ■(1)看图定限; ·(2)穿越发定限; ·(3)不等式定限
◼ 积分次序的选择 ◼ (1)可积分; ◼ (2)少分片; ◼ (3)计算简单。 ◼ 积分限的选择 ◼ (1)看图定限; ◼ (2)穿越发定限; ◼ (3)不等式定限

关于对称性问题,即关于积分I=∬f(x,y)do (1)若积分区域D关于x轴对称, 则当 f(x,-y)=-f(x,y),→I=0 f(x,-y)=f(x,y), 1=2f(.ydo D,={(x,y)∈D,y20}
关于对称性问题,即关于积分 ( , ) D I f x y d = (1)若积分区域D关于x轴对称, f x y f x y ( , ) ( , ), − = − =I 0 f x y f x y ( , ) ( , ), − = ( ) 1 1 2 ( , ) , , 0 D I f x y d D x y D y = = x y o D1 则当

(2)若积分区域D关于y轴对称, 则当 f(-x,y)=-f(x,y), 、I=0 f(-x,y)=f(x,y), D 1=2∬fx,y)do D D={(x,y)eD,x≥0}
(2)若积分区域D关于y轴对称, f x y f x y ( , ) ( , ), − = − =I 0 f x y f x y ( , ) ( , ), − = ( ) 1 1 2 ( , ) , , 0 D I f x y d D x y D x = = x y o D1 则当

(3)若积分区域D关于原点对称,则当 f(-x,-y)=-f(x,y)→I=0 1=2∬f(x,y)do f(-x,-y)=f(x,y),→ D D={(x,y)∈D,x20y≥0} (4)若积分区域D关于直线y=x对称,则 ∬fxdo=f0,xado 此式称为关于积分变量的轮换对称性
(3)若积分区域D关于原点对称,则当 f x y f x y ( , ) ( , ), − − = − =I 0 f x y f x y ( , ) ( , ), − − = ( ) 1 1 2 ( , ) , , 0, 0 D I f x y d D x y D x y = = (4)若积分区域D关于直线 y x = 对称,则 ( , ) ( , ) D D f x y d f y x d = 此式称为关于积分变量的轮换对称性
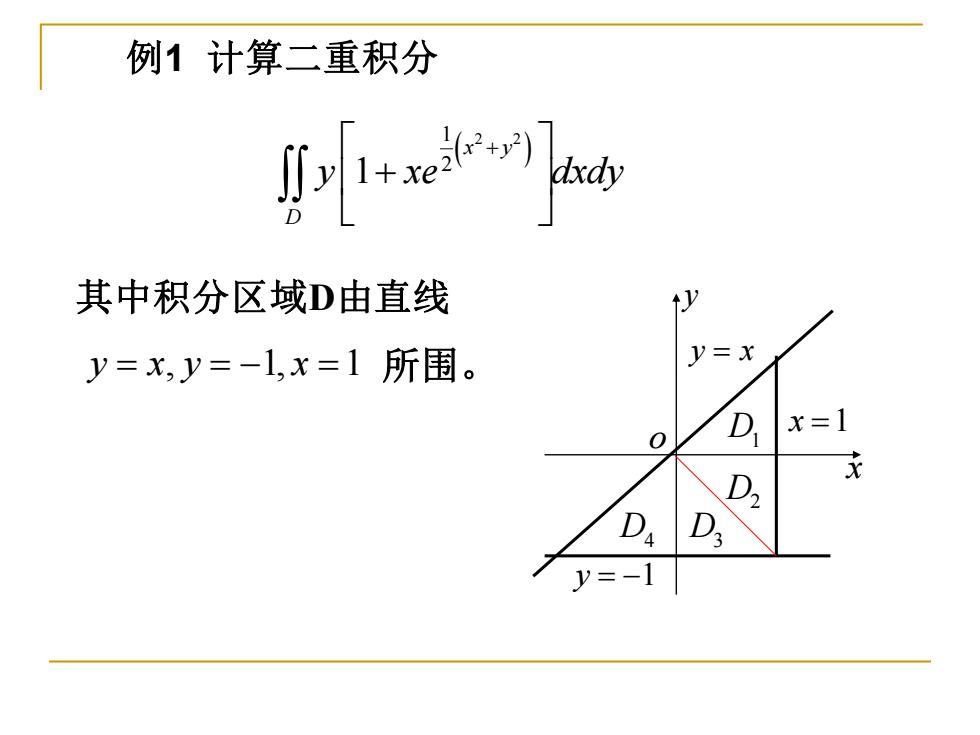
例1计算二重积分 小1e 其中积分区域D由直线 y=x,y=-1,x=1所围。 y=x D x=1 D
例1 计算二重积分 ( ) 1 2 2 2 1 x y D y xe dxdy + + 其中积分区域D由直线 y x y x = = − = , 1, 1 所围。 x y o y x = y = −1 x =1 D1 D2 D4 D3
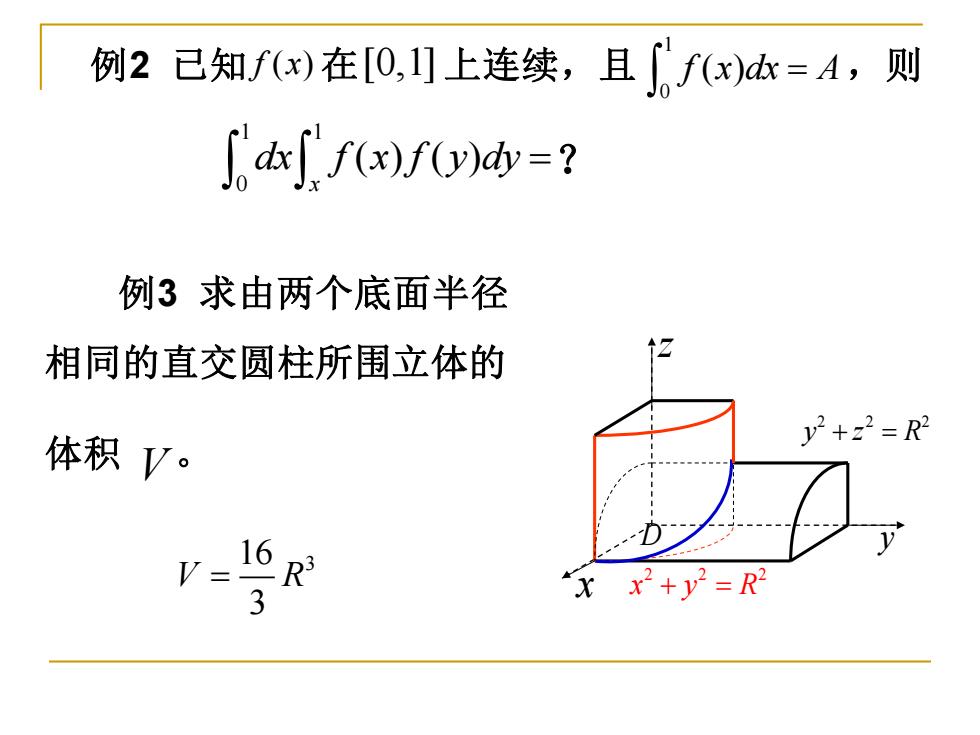
例2已知f(x)在[0,1]上连续,且fx)d=A,则 d)()dv=? 例3求由两个底面半径 相同的直交圆柱所围立体的 ↑2 +z2=R2 体积V。 V 16R3 xx+y2=R2
例2 已知 f x( ) 在 [0,1] 上连续,且 ,则 1 0 f x dx A ( ) = 1 1 0 ( ) ( ) x dx f x f y dy = ? 例3 求由两个底面半径 相同的直交圆柱所围立体的 体积 V 。 x y z 2 2 2 x y R + = 2 2 2 y z R + = D 16 3 3 V R =
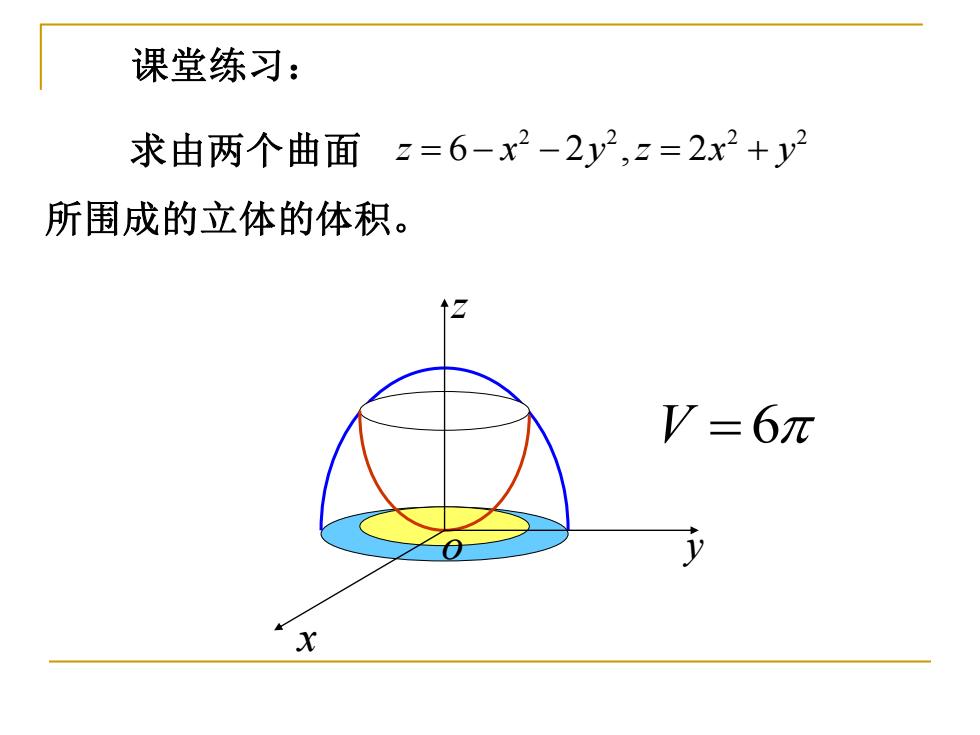
课堂练习: 求由两个曲面z=6-x2-2y2,z=2x2+y2 所围成的立体的体积。 ↑Z V=6π X
课堂练习: 求由两个曲面 所围成的立体的体积。 2 2 2 2 z x y z x y = − − = + 6 2 , 2 x y z o V = 6

例4计算二次积分 nsin 课堂练习: e+ea
例4 计算二次积分 2 4 2 1 2 sin sin 2 2 x x x x x dx dy dx dy y y + 课堂练习: 1 1 2 1 1 1 4 2 2 y y y y x x y dy e dx dy e dx +