
教学内容与教学要求 教学内容:《经济数学》第六章~第十章。 ■教学时数:1~16周,每周6学时,共96学时。 教学要求:以本教材内容为基本要求,以考研 数学四试题难度为要求上限。 ■作业要求:每周(星期一)交一次作业
教学内容与教学要求 ◼ 教学内容:《经济数学》第六章~第十章。 ◼ 教学时数: 1~16周,每周6学时,共96学时。 ◼ 教学要求:以本教材内容为基本要求,以考研 数学四试题难度为要求上限。 ◼ 作业要求:每周(星期一)交一次作业
第六章空间解析几何初步 ■本章介绍空间解析几何初步知识.首 先建立三维空间的直角坐标系,引 进向量的概念和运算。然后利用向 量工具讨论空间的平面和直线、空 间曲线和二次曲线。 ,世士世接在 以地 ■§6.1空间直角坐标系 ■一、空间点的直角坐标 ■1、空间直角坐标系的形成 ■右手系八个卦限
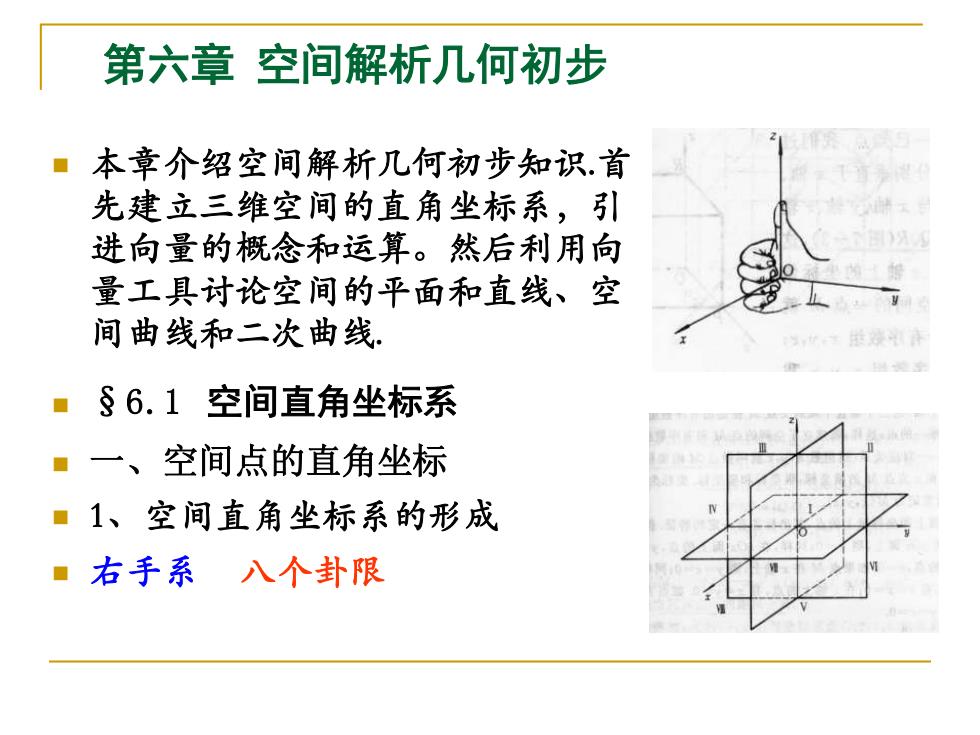
第六章 空间解析几何初步 ◼ 本章介绍空间解析几何初步知识.首 先建立三维空间的直角坐标系,引 进向量的概念和运算。然后利用向 量工具讨论空间的平面和直线、空 间曲线和二次曲线. ◼ §6.1 空间直角坐标系 ◼ 一、空间点的直角坐标 ◼ 1、空间直角坐标系的形成 ◼ 右手系 八个卦限

2、空间点的直角坐标 2 设M为空间一点,过点作三个平面分别 M 垂直于x轴、y轴和z轴,它们与x轴、y 轴、z轴的交点依次为P、Q、R,这三 1¥ 点在轴x、y轴、z轴上的坐标依次为x、 y、z.于是空间点就唯一地确定了一个有序数组。 ·反之,若已知一个有序数组x,y,:,我们可以在x轴上取 坐标为x的点P,在y轴上取坐标为y的点Q,在z轴上取坐 标为z的点R,然后通过P、Q、R分别作x轴、y轴与z轴 垂直的平面,由这三个平面得到唯一的交点M。 空问点与三元有序数组之问的一一对应关象
2、空间点的直角坐标 ◼ 设M为空间一点,过点作三个平面分别 垂直于x轴、y轴和z轴,它们与x轴、y 轴、z轴的交点依次为P、Q、R,这三 点在轴x、y轴、z轴上的坐标依次为x、 y、z.于是空间点就唯一地确定了一个有序数组。 ◼ 反之,若已知一个有序数组 ,我们可以在x轴上取 坐标为x的点P,在y轴上取坐标为y的点Q,在z轴上取坐 标为z的点R,然后通过P、Q、R分别作x轴、y轴与z轴 垂直的平面,由这三个平面得到唯一的交点M。 Q M O z R y P x x y z , , • 空间点与三元有序数组之间的一一对应关系
二、空间两点间的距离 设M,(x1,1),M2(x2y2,22)为 空间的两点,记M,M,的距离 为M,M2, d"=MMP =IMNP+INMP" =MiP+PN+NM =(x2-x)2+(2-)2+(22-2)2 空间两,点间的距离公式为: d=MM2=Vx2-x)2+(y2-)2+(22-)2 特别地,点M与坐标原,点的距离为:d=OM=√x2+y+2
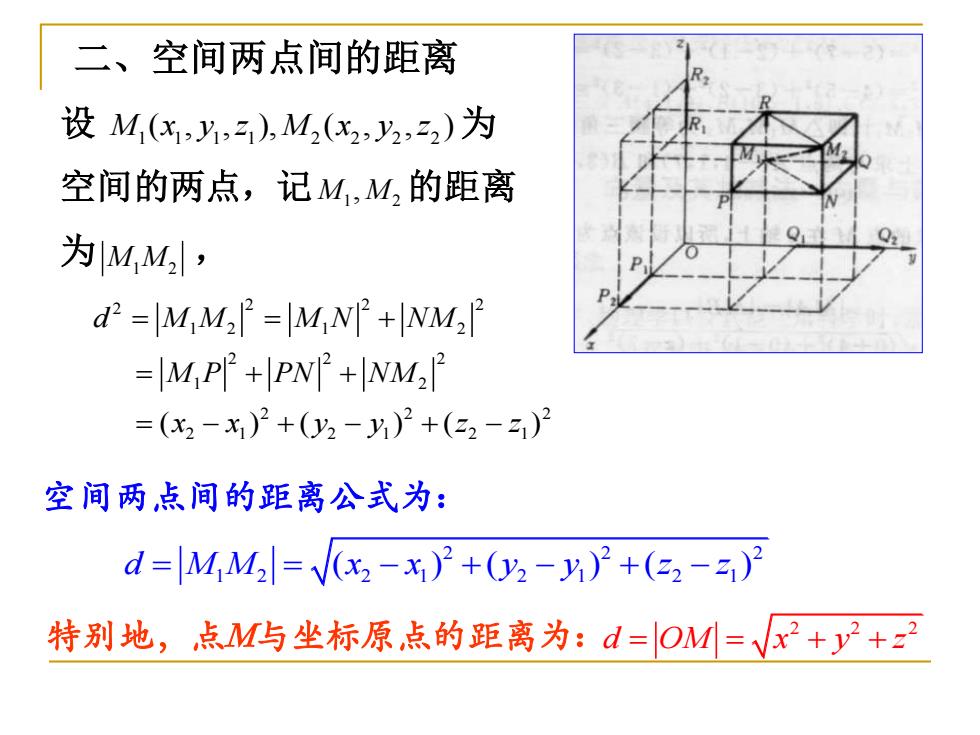
二、空间两点间的距离 设 为 空间的两点,记 的距离 为 , 1 1 1 1 2 2 2 2 M x y z M x y z ( , , ), ( , , ) 1 2 M M, M M1 2 2 2 2 2 1 2 1 2 2 2 2 1 2 2 2 2 2 1 2 1 2 1 ( ) ( ) ( ) d M M M N NM M P PN NM x x y y z z = = + = + + = − + − + − 空间两点间的距离公式为: 2 2 2 1 2 2 1 2 1 2 1 d M M x x y y z z = = − + − + − ( ) ( ) ( ) 特别地,点M与坐标原点的距离为: 2 2 2 d OM x y z = = + +

三、本节教学要求: 1.掌握空间点的坐标表示,明确不同卦限内、 坐标面上和坐标轴上的点的坐标特征。 例如:A(1,-2,3), B(2,3,-4); C(2,-3,-4); D(-2,-3,1) 第V卦限第V卦限 第Ⅷ卦限 第Ⅲ卦限 E(3,4,0):F(0,4,3);G(3,0,0);H(0,-1,0) 在xOy平面在y0z平面 在x轴 在轴 2.掌握空间两点间的距离公式,并且要能够灵 活运用距离公式计算满足特定条件的点的坐标
三、本节教学要求: 1. 掌握空间点的坐标表示,明确不同卦限内、 坐标面上和坐标轴上的点的坐标特征。 例如: A B C D (1, 2,3); (2,3, 4); (2, 3, 4); ( 2, 3,1) − − − − − − 第Ⅳ卦限 第Ⅴ卦限 第Ⅷ卦限 第Ⅲ卦限 E F G H (3,4,0); (0,4,3); (3,0,0); (0, 1,0) − 在xoy平面 在yoz平面 在x轴 在y轴 2. 掌握空间两点间的距离公式,并且要能够灵 活运用距离公式计算满足特定条件的点的坐标

例1求证:以A(1,2,3),B(2,1,4),C(4,-2,-1) 为顶点的三角形是直角三角形 解:因为 AB=(2-1)2+(1-2)2+(4-3)2=3 AC=(4-1)2+(-2-2)2+(-1-3)2=41 BC=(4-2)2+(-2-1)2+(-1-4)2=38 所以,AB2+|BC-3+38=41,又因为AC=41 根据勾股定理可知,三角形△ABC是直角三角形
例1 求证:以 A(1, 2,3) , B(2,1,4) , C(4, 2, 1) − − 为顶点的三角形是直角三角形. 2 2 2 2 2 2 2 2 2 2 2 2 (2 1) (1 2) (4 3) 3 (4 1) ( 2 2) ( 1 3) 41 (4 2) ( 2 1) ( 1 4) 38 AB AC BC = − + − + − = = − + − − + − − = = − + − − + − − = 所以, 2 2 AB BC + = + = 3 38 41 ,又因为 2 AC = 41 根据勾股定理可知,三角形⊿ ABC 是直角三角形. 解: 因为

§6.2向量代数 一、向量的概念 ■应用学科中所遇到的量,通常可以分为两类.一类量 叫做数量另一类叫做向量(也称失量)· ■在数学上,通常用一条有方向的线段,即有向线段来 表示向量。有向线段的长度表示向量的大小,有向线 段的方向表示向量的方向。如以A为起,B为终点的 向量,记作AB,向量可用一个上面带箭头的字母来表 示,如ā,b,c等,或用一个粗体的字母表示
§6.2 向量代数 ◼ 一、向量的概念 ◼ 应用学科中所遇到的量,通常可以分为两类. 一类量 叫做数量.另一类叫做向量(也称矢量). ◼ 在数学上,通常用一条有方向的线段,即有向线段来 表示向量。有向线段的长度表示向量的大小,有向线 段的方向表示向量的方向。如以A为起,B为终点的 向量,记作 ,向量可用一个上面带箭头的字母来表 示,如 等,或用一个粗体的字母表示。 AB a b c ,
■ 向量的大小或长度称为向量的模,记做AB、d或4。 向量的特征是大小和方向,所以,当两个向量的大小 相等、方向相同时,就称这两个向量相等。两个相等的 向量不一定起点相同,但是,经过平行移动后它们一定 能够完全重合。 二、向量的运算 1.向量的加法 c=a+b B
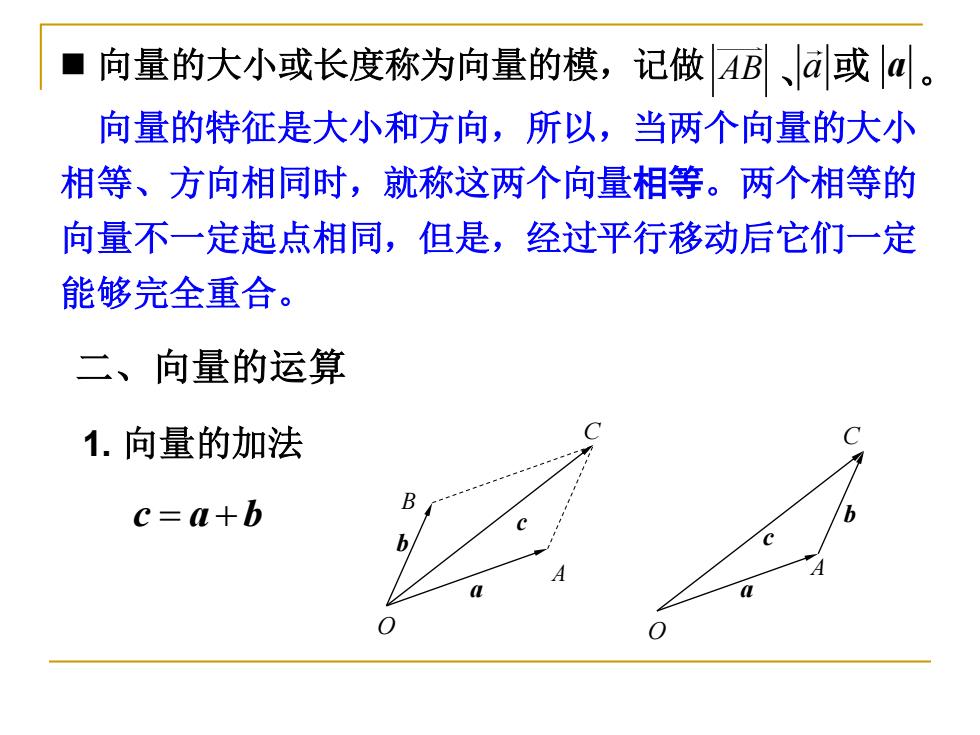
◼ 向量的大小或长度称为向量的模,记做 AB a 向量的特征是大小和方向,所以,当两个向量的大小 相等、方向相同时,就称这两个向量相等。两个相等的 向量不一定起点相同,但是,经过平行移动后它们一定 能够完全重合。 、 或 a 。 二、向量的运算 1. 向量的加法 C c A B O a b A C O a b c c a b = +

向量的加法符合交换律和结合律: 1.交换律a+b=b+a; 2.结合律(a+b)+c=+(b+c)=M+b+c 设a为一向量,与a模相同而方向相反的向量叫做a 的负向量,记做-。 我们规定两个向量a与b的差:a-b=a+(-b) 显然a-a=a+(-)=0 式中0表示模等于零的向量,这样的向量叫做零向量, 零向量的方向可看作是任意的
1.交换律 a+b=b+a; 2.结合律 (a+b)+c=a+(b+c)=a+b+c. a b a b − = + −( ) 显然 ( ) 0 a a a a − = + − = 式中0表示模等于零的向量,这样的向量叫做零向量, 零向量的方向可看作是任意的. 设a为一向量,与a 模相同而方向相反的向量叫做a 的负向量,记做-a。 我们规定两个向量a与b的差: 向量的加法符合交换律和结合律:

2.向量与数量的乘积 设几是一个数,向量与九的乘积九a规定为: (1)元>0时,a与a同向,|2a=a: (2)元=0时,λa=0; (3)元<0时,入a与a反向,|2a=2lal。 向量与数量的乘积符合下列运算规律: 1.结合律(ua)=u(入a)=()a; 2.分配率(入+)M=人a+uM; 3.分配率(a+b)=M+2b
2. 向量与数量的乘积 设 是一个数,向量a与 的乘积 a规定为: 向量与数量的乘积符合下列运算规律: (1) 0 时, a与a同向, | | | | a a = ; (2) = 0 时, a = 0 ; (3) 0 时, a与a反向, | | | | a a = 。 1. 结合律 ( ) ( ) ( ) a a a = = ; 2.分配率 ( ) + = + a a a ; 3.分配率 ( ) a b a b + = +