
上次课内容复习 1.二重积分的定义 J小nf(x,)do=lm∑f5,n)Ao 入→0 i=1 2.二重积分的性质(与定积分性质相似)
上次课内容复习 1. 二重积分的定义 D f (x, y)d i i i n i f = = → lim ( , ) 1 0 2. 二重积分的性质 (与定积分性质相似)

§8.2二重积分的计算 由曲顶柱体体积的计算可知,当被积函数f(x,y)≥0 且在D上连续时,若D为X-型区域 yy=02(x) 9965se到 a≤x≤b 则 心,dd=drd y=o(x)bx 若方区D2 x=Ψ2(y) c≤y≤d x=V(y) 则fx,dndv=ayf
§8.2 二重积分的计算 且在D上连续时, 当被积函数 f (x, y) 0 a x b x y x D ( ) ( ) : 1 2 D f (x, y)dxdy f x y y x x ( , )d ( ) ( ) 2 1 = b a d x 由曲顶柱体体积的计算可知, 若D为 X – 型区域 则 ( ) 1 y = x ( ) 2 y = x o b x y D a x 若D为Y –型区域 c y d y x y D ( ) ( ) : 1 2 y ( ) 1 x = y ( ) 2 x = y x d o c y f x y x y y ( , )d ( ) ( ) 2 1 d c 则 d y

当被积函数f(x,y)在D上变号时,由于 .)f(x.y)-fx.) 2 2 (x,y) f2(x,y)均非负 f)dxdy=(y)dxdy -∬nJ2(x,)dxdy 因此上面讨论的累次积分法仍然有效
当被积函数 f (x, y) − + = 2 ( , ) ( , ) ( , ) f x y f x y f x y 2 f (x, y) − f (x, y) ( , ) 1 f x y ( , ) 2 f x y 均非负 在D上变号时, 因此上面讨论的累次积分法仍然有效 . 由于

说明:(①)若积分区域既是X-型区域又是Y-型区域, 则有 ∬nf(x,y)dxdy d -axrcd x必y r=2(y) y 1 dx 0 a b x 为计算方便,可选择积分序,必要时还可以交换积分序 (2)若积分域较复杂,可将它分成若干 X型域或Y型域,则 川。=川。+。+n
o x y 说明: (1) 若积分区域既是X–型区域又是Y –型区域 , D f (x, y)dxdy 为计算方便,可选择积分序, 必要时还可以交换积分序. ( ) 2 y = x o x y D a b ( ) 1 x = y ( ) 2 x = y d c 则有 x ( ) 1 y = x y f x y y x x ( , )d ( ) ( ) 2 1 = b a d x f x y x y y ( , )d ( ) ( ) 2 1 = d c d y (2) 若积分域较复杂,可将它分成若干 D1 D2 D3 X-型域或Y-型域 , = + + D D1 D2 D3 则
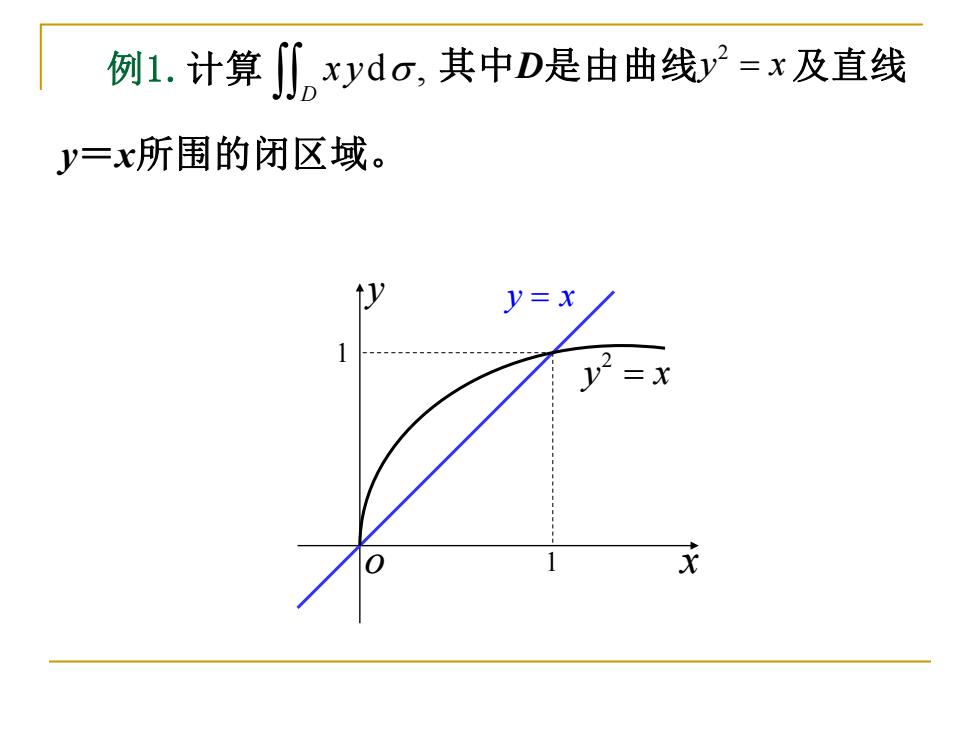
例1.计算∬xyda,其中D是由曲线y=x及直线 y=x所围的闭区域。 1) 元
例1.计算 d , D x y 其中D是由曲线 及直线 y=x所围的闭区域。 2 y x = x y o 2 y x = y x = 1 1
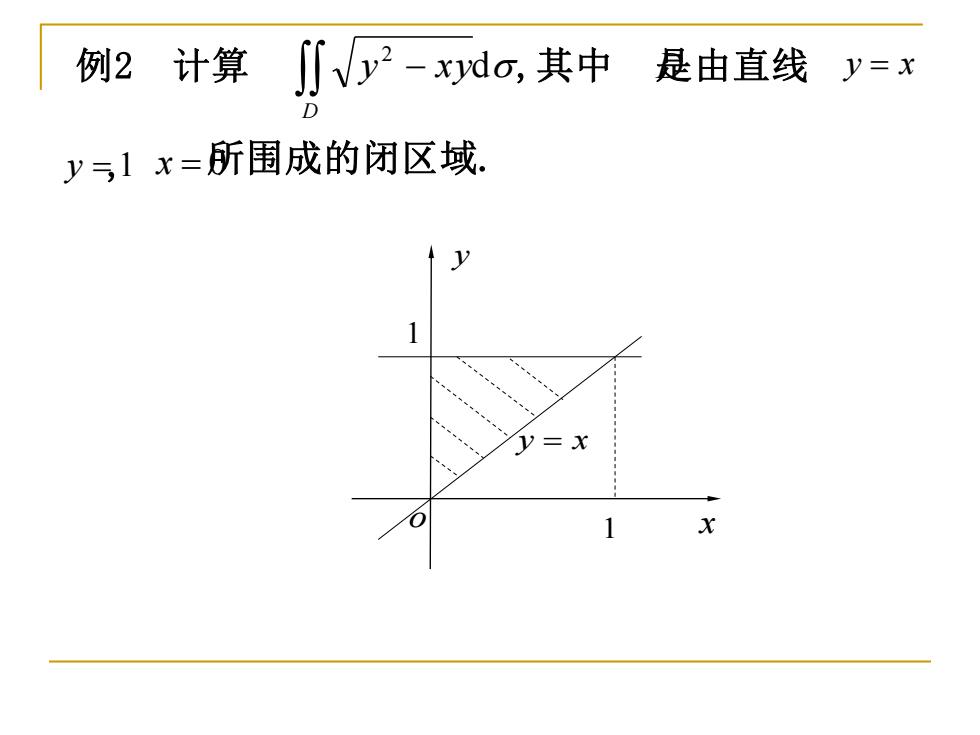
例2计算 ∬V少2-xdo,其中是由直线 y=x D y51x=所围成的闭区域。 V=X
− D y x yd 2 D y x = y = 1 x = 0 例2 计算 ,其中 是由直线 , 所围成的闭区域. o x 1 1 y x = y

例3.计算川Dx心o,其中D是抛物线 y2=x 及直线y=x-2所围成的闭区域. (4,2) (4.2) y=x 2 x=y+2 4 x (1,-1) (1,-1)
例3. 计算 d , D xy 其中D 是抛物线 及直线 所围成的闭区域

例4计算[eda其中D是由y=x,y=0及 x=1所围成的区域。 EX:8-21,2,3 例5计算二次积分 1-女sdr 例6计算小川2-xdo,其中 D={(x,y)川0≤x≤1,0≤y≤1}
例4 计算 其中D 是由 及 所围成的区域。 2 x D e d − y x y = = , 0 x =1 例5 计算二次积分 − − − = + 1 2 2 2 1 e 0 e e e e e d ln 1 d d ln 1 I d x x x y x y y − D | y x | d 2 D = {( x, y) | 0 x 1, 0 y 1} 例6 计算 ,其中 EX:8-2 1,2,3