
§9.3任意项级数及其审敛法 一、交错级数及其审敛法 如果级数的各项是正、负交错的,也就是说, 级数具有下面的形式: 山1一2+儿3-4+. 或 -w1+u2-u3+4- 其中 u1,2 都是正数,把这样的级数称为交错级数
u1 −u2 +u3 −u4 + 或 − u1 + u2 − u3 + u4 − 其中 u1 , u2 , 都是正数,把这样的级数称为交错级数. 一、交错级数及其审敛法 §9.3 任意项级数及其审敛法 如果级数的各项是正、负交错的,也就是说, 级数具有下面的形式:

定理1(莱布尼茨定理Leibnitz) 如果交错级数 ∑(-14n(4,>0,n=1,2,3,) h- 满足条件:(I)4n≥um+l (n=1,2,3,.; (2)lim u=0。 则级数 ∑(-1)”收敛,且其和S≤4用它的部 n=1 分和S,作为级数和S的近似值,误差 小Sn-≤4n+1
定理1 (莱布尼茨定理Leibnitz) = − − 1 1 ( 1) n n n u ( 0, 1,2,3, ) n u n = ( 1,2,3, ) un un+1 n = lim = 0 → n n u = − − 1 1 ( 1) n n n u 1 s u n s s n − un+1 s s 满足条件: (2) 则级数 收敛,且其和 ,用它的部 (1) ; 分和 作为级数和 的近似值,误差 。 。 如果交错级数
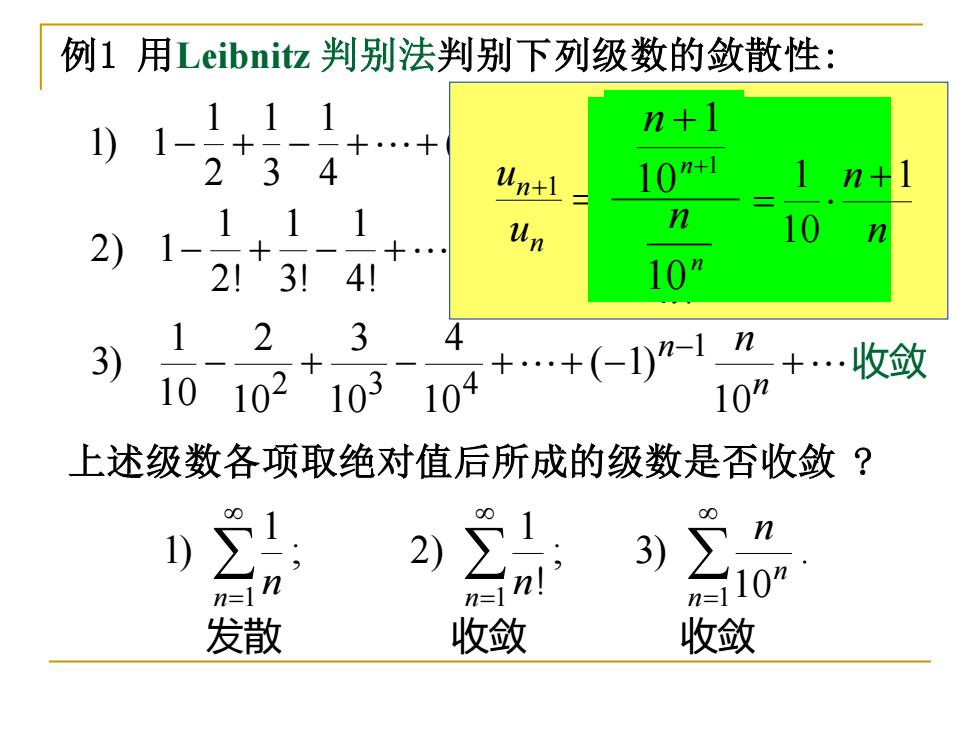
例1用Leibnitz判别法判别下列级数的敛散性: 111 1) 1 n+1 4 Un+l 10+ n+] n 2) 1 Un n 41 10” 3) ,3 .+(-1)n-1n +.收敛 10 102103104 10n 上述级数各项取绝对值后所成的级数是否收敛? 1 3) 发散 收敛 收敛
收敛 收敛 − + − ++ − − + n n 1 ( 1) 4 1 3 1 2 1 1) 1 1 − + − ++ − − + ! 1 ( 1) 4! 1 3! 1 2! 1 2) 1 1 n n 例1 用Leibnitz 判别法判别下列级数的敛散性: − + − ++ − n− n + n 10 ( 1) 10 4 10 3 10 2 10 1 3) 1 2 3 4 收敛 ; 1 1) 1 n= n ; ! 1 2) 1 n= n . 10 3) 1 n= n n 发散 收敛 收敛 ( 1)! 1 n + ! 1 n 1 1 + = n = + n n u u 1 10 1 +1 + n n n n 10 n n 1 10 1 + = 上述级数各项取绝对值后所成的级数是否收敛 ?

二、绝对收敛与条件收敛 0 定义:对任意项级数∑4n,若∑4n收敛, n=1 n=l 则称原级数∑山绝对收敛 n=1 若原级数收敛,但取绝对值以后的级数发散, 则称原级数∑4n条件收敛 n=1 例如:∑(-1)-11 00 为条件收敛. n=l n ∑(-1)-11 ∑(-)-1 均为绝对收敛、 n三 n=1 10
二、绝对收敛与条件收敛 定义:对任意项级数 若 若原级数收敛, 但取绝对值以后的级数发散, = − − 1 1 1 ( 1) n n n = − − 1 1 10 ( 1) n n n n 收敛 , 为条件收敛 . 均为绝对收敛. 例如 : 则称原级数 绝对收敛 ; 则称原级数 条件收敛

定理2如果级数 ∑绝对收敛,则级数 ∑4 n- 必定收敛 证:设∑u,收敛令(4n+4,(n=1,2,) n=l 显然yn≥0,且Vn≤4n,根据比较审敛法∑yn收敛 n= un 2Vn un 4,22,收敛 n=1 n=l 0 ∑4,也收敛 n=l
n=1 n u n=1 定理2 如果级数 绝对收敛,则级数 un 必定收敛. 证: 设 n v (n =1, 2 , ) 显然 vn 0 , 根据比较审敛法 n=1 n v 收敛, 收敛 =1 2 n n v n n un u = 2v − , 1 n= n u n=1 n u 也收敛 ( ) 2 1 = un + un 且 n v , un 收敛 ,令

例2判别级数 sin na. 2 的收敛性 n=1 n 例3判别级数 1 1.11 十 In2 In3 In4 In5 的收敛性.如果收敛,是绝对收敛还是条件收敛? 课堂练习:证明下列级数绝对收敛 n=
例2 判别级数 =1 2 sin n n n 的收敛性. 例3 判别级数 − + − + ln 5 1 ln 4 1 ln 3 1 ln 2 1 的收敛性.如果收敛,是绝对收敛还是条件收敛? 课堂练习:证明下列级数绝对收敛 2 1 ( 1) . n n n n e = −

2 Un en, (n+1)2 lim=lim n→ooln n>∞ n2 =mt -r收效四t子小 绝对收敛 n=i n=l
令 n n n u u 1 lim + → lim → = n 1 2 ( 1) + + n e n n e n 2 2 1 1 lim + = → n n n e 1 1 = e 因此 = − 1 2 ( 1) n n n e n = − 1 2 ( 1) n n n e n 收敛, 绝对收敛

定理3绝对收敛级数不因改变项的位置而改变它 的和(绝对收敛级数具有可交换性)。 定理4(绝对收敛级数的乘法)设级数 00 ∑ 都绝对收敛,它们的和分别为和石,则它们 n=l 的柯西乘积 4y1+(42+u2y1)+. +(u1n+2Vm-1+.+uny1). 也是绝对收敛的,且其和为5·O
定理3 绝对收敛级数不因改变项的位置而改变它 的和(绝对收敛级数具有可交换性)。 n=1 n u n=1 n v s u1 v1 + (u1 v2 + u2 v1 ) + + (u1 vn + u2 vn−1 ++ un v1 ) s 定理4(绝对收敛级数的乘法) 设级数 及 都绝对收敛,它们的和分别为 和 ,则它们 的柯西乘积 也是绝对收敛的,且其和为
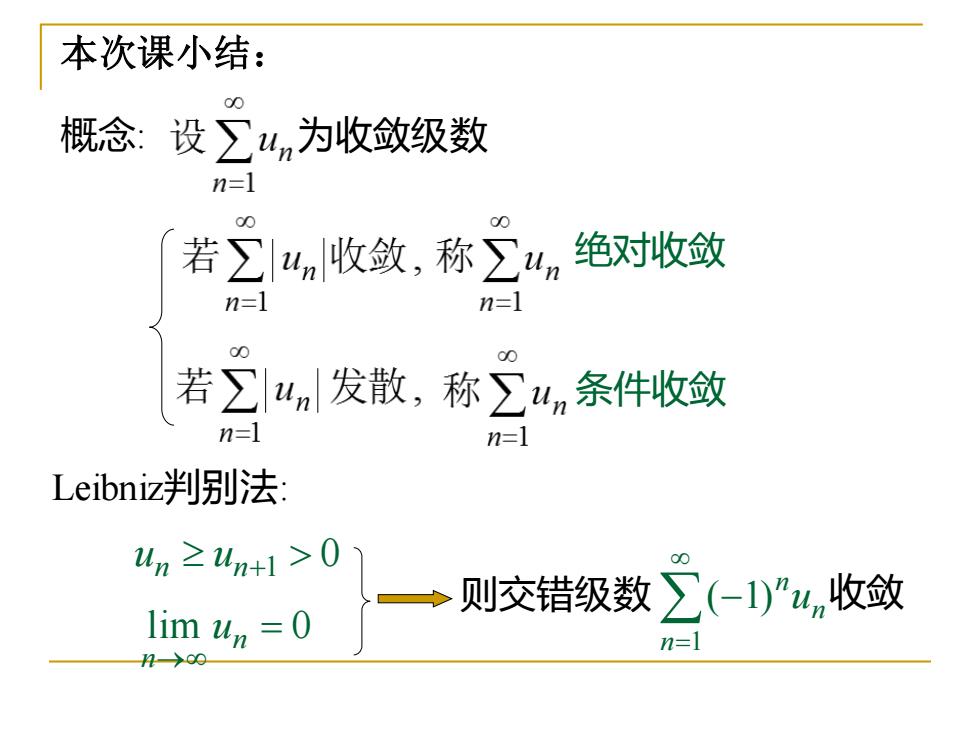
本次课小结: 概念: 设∑4n为收敛级数 n=1 若∑4a收敛,称∑4n 绝对收敛 n=1 n=l 00 00 若∑un发散,称∑4n条件收敛 n=1 n=1 Leibniz判别法: un≥un+l>0) 则交错级数∑(-1)”un收敛 lim un =0 n=1 h→o0
本次课小结: 为收敛级数 Leibniz判别法: un un+1 0 lim = 0 → n n u 则交错级数 n n n u = − 1 ( 1) 收敛 概念: 绝对收敛 条件收敛

思考与练习 作业:EX9-3 00 设正项级数 ∑4,收敛,能否推出∑收敛? n=l n=l 2 提示:lim=lm,=0 n-→ooln n->o0 ●● 由比较判敛法可知∑收敛. n= 注意:反之不成立.例如, 2收敛,发散。 n=1 n=1h
思考与练习 设正项级数 n=1 n u 收敛, 能否推出 =1 2 n n u 收敛 ? 提示: n n n u u 2 lim → n n u → = lim = 0 由比较判敛法可知 =1 2 n n u 收敛 . 注意: 反之不成立. 例如, =1 2 1 n n 收敛 , =1 1 n n 发散 . 作业:EX 9-3