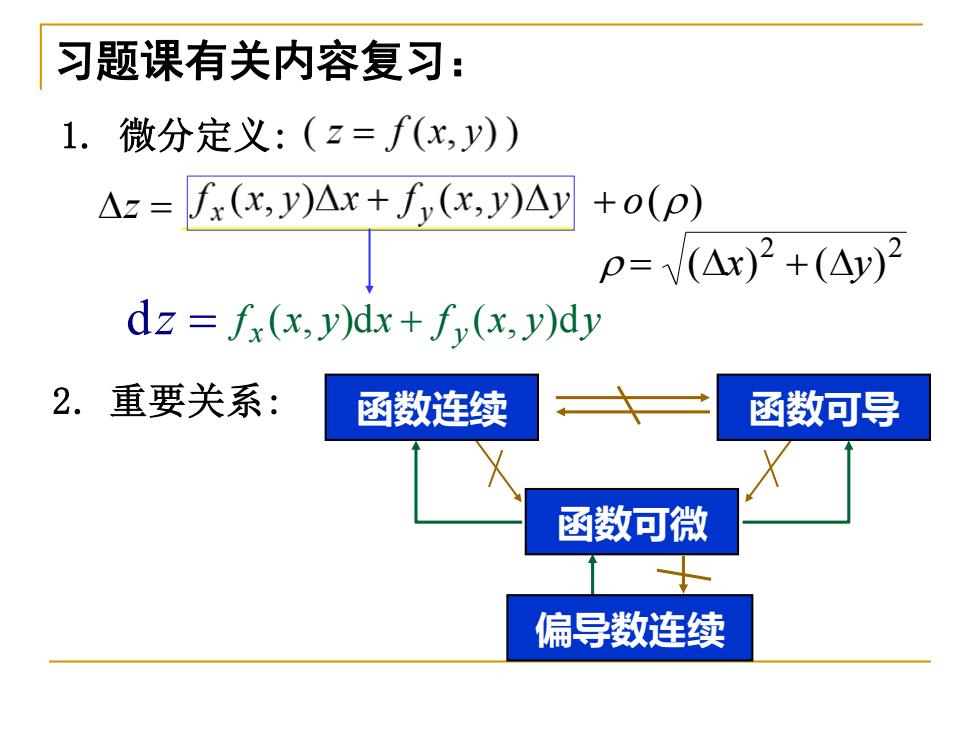
习题课有关内容复习: 1.微分定义:(z=f(x,y)) Az=fx(x,y)Ax+fy(x,y)Ay +0(P) p=V(△x)2+(△y)2 dz=fx(x,y)dx+fy(x,y)dy 2.重要关系: 函数连续 函数可导 函数可微 偏导数连续
习题课有关内容复习: 1. 微分定义: z = dz = f x y x f x y y x ( , )d + y ( , )d 2 2 = (x) + (y) 2. 重要关系: + o() 函数可导 函数可微 偏导数连续 函数连续

3.微分应用 ·近似计算 △Z≈fx(x,y)△x+f(x,y)A) f(x+△x,y+△y) ≈f(x,y)+fx(x,y)△x+f(x,y)A
3. 微分应用 • 近似计算 f x y x f x y y x ( , ) + y ( , ) f x y x f x y y x ( , ) + y ( , )
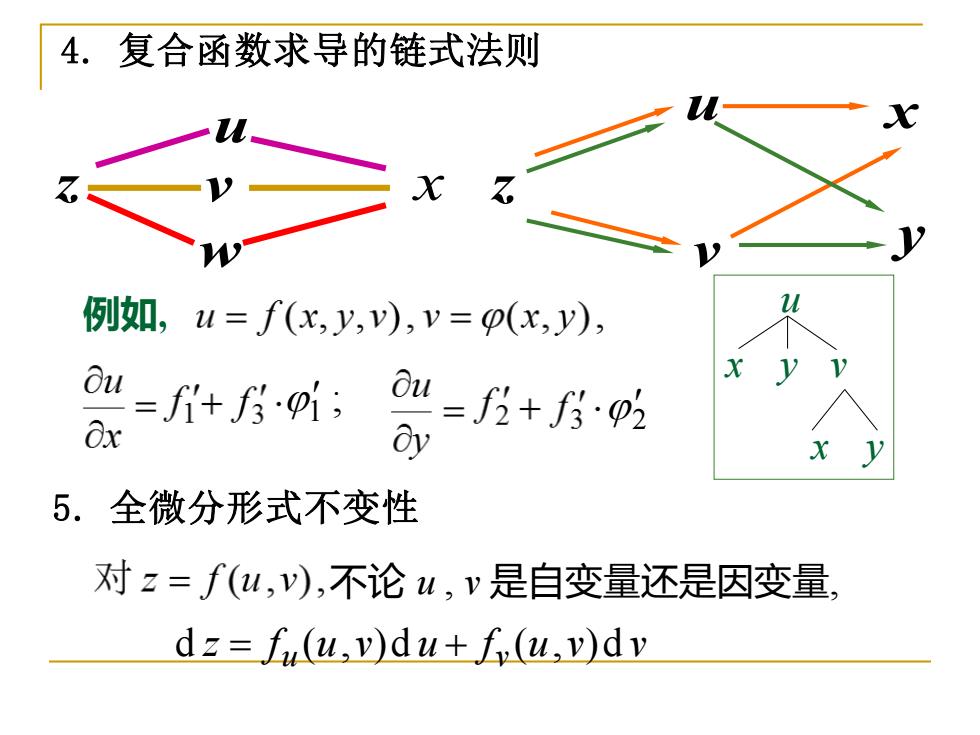
4.复合函数求导的链式法则 例如,u=f(x,y,),v=p(x,y), =f+6p听;=f乃+f5p时 8x Oy 5.全微分形式不变性 对z=f(u,),不论u,v是自变量还是因变量, dz=f (u,v)du+f(u,v)dv
4. 复合函数求导的链式法则 例如, u x y v x y ; 1 2 z u v w x z u v x y 5. 全微分形式不变性 不论 u , v 是自变量还是因变量, z f u v u f u v v d = u ( , )d + v ( , )d

习题中的若干问题解析 1、试定义下列函数在原点的值,使其在该点连 续。P198,EX8) tan(x2+y2) f(x,y)= 1-cosx2+y2 2、证明下列函数在原点处偏导数存在但不连 续。(P203EX6) ,x2+y2≠0 0x2+y2=0
习题中的若干问题解析 1、试定义下列函数在原点的值,使其在该点连 续。(P198,EX8) 2 2 2 2 tan( ) ( , ) 1 cos x y f x y x y + = − + 2、证明下列函数在原点处偏导数存在但不连 续。(P203EX6) 2 2 2 2 4 2 2 , 0 ( , ) 0 0 xy x y f x y x y x y + = + + =

3、证明函数f(x,y)=Vy在点(0,0)处不可微。 (P207EX7) 课堂练习题一 2、设z=xe+y+(x+l)ln(1+y),求:dl0。 (2005年数四考题,4分)
3、证明函数 f x y xy ( , ) = 在点(0,0)处不可微。 (P207EX7) 课堂练习题一 1、设 1 z x u y = ,求: (1,1,1) du 。 2、设 e ( 1)ln(1 ) x y z x x y + = + + + ,求: (1,0) dz 。 (2005年数四考题,4分)

3、设f四可微,且f0=5, 求函数 z=f(4x2-y2)在点(1,2)处的全微分。 (2006年数四考题,4分) 例1设f(u.)具有二阶连续偏导数,且满足 0f+0f-1,又gxW=wx-y广】 020v2 求:( g 。(2003年数四考题,8分) 0x2 0y2
3、设 可微,且 ,求函数 在点 处的全微分。 f u( ) 1 (0) 2 f = 2 2 z f x y = − (4 ) (1, 2) (2006年数四考题,4分) 例1 设 f u v ( . ) 具有二阶连续偏导数,且满足 2 2 2 2 1 f f u v + = ,又 1 2 2 ( , ) [ , ( )] 2 g x y f xy x y = − 求: 2 2 2 2 g g x y + 。(2003年数四考题,8分)

例2设z=fy,+g )其中f具有二阶 连续偏导数,8具有二阶连续导数,求: axoy 课堂练习题二 1、设z=e,x=cost,y=tsint,.求: dz 工、设他二元可微,=作学求会 02 (2007年数四考题,4分)
例2 设 其中 具有二阶 连续偏导数, 具有二阶连续导数,求 。 ( , ) ( ) x y z f xy g y x = + f g 2 z x y 课堂练习题二 1、设 2 , cos , sin , xy z e x t t y t t = = = 求: 2 t dz dt = 2、设 f u v ( , ) 二元可微, ( , ) ,求: y x z f x y = z z x y x y − (2007年数四考题,4分)

3、设z=f(2x-y,ysinx),其中f(u,v)具有 二阶连续偏导数,求:2: 8xoy (1990年数四考题,5分) 4、设z=f(e*sin y,x2+y2),其中f(u,v)具有 二阶连续偏导数,求: Oxoy (1992年数四考题,5分)
3、设 z f x y y x = − (2 , sin ) ,其中 具有 二阶连续偏导数,求: f u v ( , ) 2 z x y 。 (1990年数四考题,5分) 4、设 2 2 ( sin , ) x z f e y x y = + ,其中 具有 二阶连续偏导数,求: f u v ( , ) 2 z x y 。 (1992年数四考题,5分)

5、设f)具有二阶连续导数,且x川=f的+f( 求:r202g 10'g Ov? 作业:综合练习七 (2005年数四考题,8分) 6、设2=f(x,y)在点(1,1)处可微,且f(1,1)=1 =2, =3,p(x)=fx,f(x,x): axlaD 1,1) 求: d p3(x) (2001年数四考题,6分)
5、设 f u( ) 具有二阶连续导数,且 ( , ) ( ) ( ) y x g x y f yf x y = + 求: 2 2 2 2 2 2 g g x y x y − 。 (2005年数四考题,8分) 6、设 z f x y = ( , ) 在点 (1,1) 处可微,且 f (1,1) 1 = (1,1) (1,1) 2, 3, ( ) ( , ( , )), f f x f x f x x x y = = = 求: 3 1 d ( ) d x x x = (2001年数四考题,6分) 作业:综合练习七

6 设函数z=f(x,y)在点(1,1)处可微,且 f(1,1)=1, of =2, =3, 0x1,1) ay1,1) 小-.求品0,e考翻 解:由题设p(1)=f(1,f(1,1)=f1,1)=1 po以k-1o28-l =3[f(x,f(x,x) +fx,fx,x)x,9+f5,)川x=l =3.[2+3·(2+3)]=51
6 (1) = f (1, f (1,1)) 1 ( ) d d 3 x = x x = f (1,1) =1 d 1 d 3 ( ) 2 = = x x x = 3 ( , ( , )) 1 f x f x x ( , ( , ))( ) 2 + f x f x x x =1 = 3 = 51 f (1,1) =1, (x) = f (x, f ( x, x)), 2, (1,1) = x f 求 设函数 在点 处可微 , 且 3, (1,1) = y f 解: 由题设 2 + 3(2 + 3) (2001考研)