
2008级第一学期《经济数学》期末考试复习提纲 ■基本概念要求 理解并熟练掌握函数的四种特性,即单调性、奇偶性、有 界性和周期性; ■熟悉分段定义函数; ·理解极限的定义,理解极限的唯一性、有界性、保号性; 。理解无穷小的概念、等价无穷小的性质; 。 理解极限存在的两个准则并会应用这两个准则证明极限的 存在性; ·理解并熟练掌握函数的连续性定义、间断点的分类; ·熟悉闭区间上连续函数的性质 ·理解导数、左右导数的定义;
2008级第一学期《经济数学》期末考试复习提纲 ◼ 基本概念要求 ◼ 理解并熟练掌握函数的四种特性,即单调性、奇偶性、有 界性和周期性; ◼ 熟悉分段定义函数; ◼ 理解极限的定义,理解极限的唯一性、有界性、保号性; ◼ 理解无穷小的概念、等价无穷小的性质; ◼ 理解极限存在的两个准则并会应用这两个准则证明极限的 存在性; ◼ 理解并熟练掌握函数的连续性定义、间断点的分类; ◼ 熟悉闭区间上连续函数的性质 ◼ 理解导数、左右导数的定义;

2008级第一学期《经济数学》期末考试复习提纲 理解函数微分的定义及其近似公式; 。 理解微分中值定理并熟悉三个定理的条件、结论; 熟练掌握函数的单调性与极值、凹凸性与拐点的判定定理 和方法: ·理解并掌握原函数与不定积分的概念和性质; ■理解定积分的定义、定积分存在的必要条件和充分条件: ·理解并掌握定积分的性质特别是估值定理和积分中值定理; 理解并掌握变限积分的定义和性质,理解并掌握牛顿一莱 布尼兹公式; 理解并掌握定积分应用的元素法; 理解两类广义积分的定义及其敛散性
2008级第一学期《经济数学》期末考试复习提纲 ◼ 理解函数微分的定义及其近似公式; ◼ 理解微分中值定理并熟悉三个定理的条件、结论; ◼ 熟练掌握函数的单调性与极值、凹凸性与拐点的判定定理 和方法; ◼ 理解并掌握原函数与不定积分的概念和性质; ◼ 理解定积分的定义、定积分存在的必要条件和充分条件; ◼ 理解并掌握定积分的性质特别是估值定理和积分中值定理; ◼ 理解并掌握变限积分的定义和性质,理解并掌握牛顿—莱 布尼兹公式; ◼ 理解并掌握定积分应用的元素法; ◼ 理解两类广义积分的定义及其敛散性

2008级第一学期《经济数学》期末考试复习提纲 ·基本运算和论证能力要求 ·熟练掌握求极限的基本方法,如四则运算法则、极限存在 法则、两个重要极限、等价无穷小代换、洛比达法则等; ·熟练掌握求导的基本方法,如复合函数求导、隐函数求导、 参数方程确定的函数的求导、对数求导法、高阶导数等; 熟练掌握分段定义函数在分段点可导性的讨论方法; ·能够运用微分中值定理和函数的单调性证明某些不等式, 运用微分中值定理证明某些方程的根的存在性和唯一性; ·能够运用导数的知识对函数的性态进行分析,熟练掌握函 数图形的描绘;
2008级第一学期《经济数学》期末考试复习提纲 ◼ 基本运算和论证能力要求 ◼ 熟练掌握求极限的基本方法,如四则运算法则、极限存在 法则、两个重要极限、等价无穷小代换、洛比达法则等; ◼ 熟练掌握求导的基本方法,如复合函数求导、隐函数求导、 参数方程确定的函数的求导、对数求导法、高阶导数等; ◼ 熟练掌握分段定义函数在分段点可导性的讨论方法; ◼ 能够运用微分中值定理和函数的单调性证明某些不等式, 运用微分中值定理证明某些方程的根的存在性和唯一性; ◼ 能够运用导数的知识对函数的性态进行分析,熟练掌握函 数图形的描绘;

2008级第一学期《经济数学》期末考试复习提纲 熟练掌握函数的极值、最大值、最小值问题的求解方法, 特别是经济类问题; ·熟练掌握不定积分的基本求解方法,特别是第一、二类换 元积分法、分部积分法等; ·熟练掌握定积分的基本求解方法,熟练掌握变限积分有关 问题的求解方法: ■熟练掌握定积分的几何应用,特别是在直角坐标系下的面 积、体积的计算,在经济问题中的应用。 理解并掌握广义积分的定义、审敛和计算方法
2008级第一学期《经济数学》期末考试复习提纲 ◼ 熟练掌握函数的极值、最大值、最小值问题的求解方法, 特别是经济类问题; ◼ 熟练掌握不定积分的基本求解方法,特别是第一、二类换 元积分法、分部积分法等; ◼ 熟练掌握定积分的基本求解方法,熟练掌握变限积分有关 问题的求解方法; ◼ 熟练掌握定积分的几何应用,特别是在直角坐标系下的面 积、体积的计算,在经济问题中的应用。 ◼ 理解并掌握广义积分的定义、审敛和计算方法
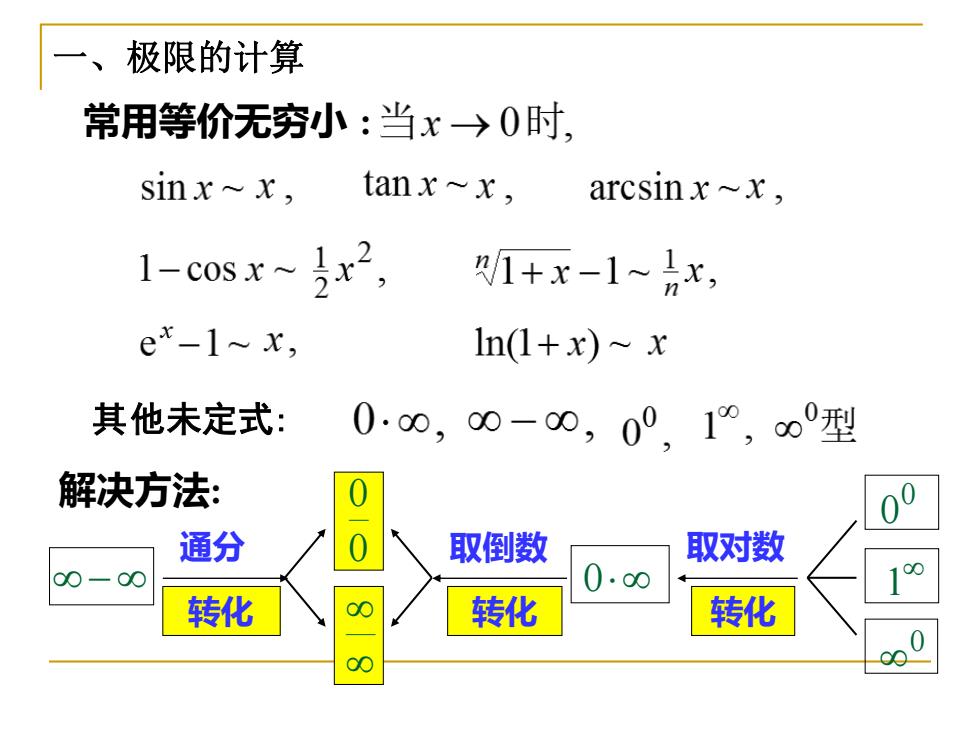
一、极限的计算 常用等价无穷小:当x→0时, sinx~x, tanx~x, arcsinx~x, 1-c0sx~x2, /1+x-1~x, n ex-I~x, In(1+x)~x 其他未定式: 0.00,00-00,00,1,0型 解决方法: 00 通分 取倒数 取对数 00-00 0.00 转化 转化 转化
一、极限的计算 常用等价无穷小 : 其他未定式: 解决方法: 通分 转化 0 0 0 取倒数 转化 0 0 1 0 取对数 转化 −

例题选解:04年考题 1. mL+产=e3,则k= X 2.已知x→0时,(1+ax2)3-1与cosx-1为等价无穷小 量,则a= 3.当x→0时,e*-1-sinx是x2的 无穷小。 te'dt 4.求lim x-→0 2x2
例题选解:04年考题 3 5 lim (1 ) e x k x x + = 1. → ,则 k = (1 ) 1 3 1 2 2. 已知 时, + ax − 与 为等价无穷小 量,则 x →0 cos x −1 a = x →0 e x x −1−sin 2 3.当 时, 是 x 的 无穷小。 2 0 0 2 lim 2 2 x te dt x t x → + 4.求

例题选解:05年考题 1 1.lim xsin 2.若要函数f)=x-+3在x=0处连续, 则应补充定义f(0)= 3.设函数f(x)在x=a可导,则四 f(a+h)-f(a-h)= h arctan tdt 4.求lim 5.求 lim x→0 3x2 x2-1
例题选解:05年考题 1 lim sin x x → x 1. = 1 1 ( ) x x f x x − − + = x = 0 f (0) 2. 若要函数 在 则应补充定义 =_ 处连续, f x( ) x a = 0 ( ) ( ) lim h f a h f a h → h + − − 3. 设函数 在 可导,则 =_ 0 2 0 arctan lim 3 x x tdt → x 4. 求 2 2 lim 1 x x x → x − 5.求

例题选解:06年考题 1、设x→0时,sinx-x与x"是同阶无穷小,则n= a+bx2,x≤0 2、若函数f(x)= sin bx 在(-0,+o0)内连续,则 ,x>0 a与b的关系是(). tanx-sinx 3.求lim x>0 3 4.求lim xtanx ex-1 →0+
x →0 sin x x − n 1、设 时, 与 x 是同阶无穷小,则 n = 例题选解:06年考题 2 , 0 ( ) sin , 0 a bx x f x bx x x + = ( , ) − + a b 2、若函数 在 内连续,则 与 的关系是( ). 0 3 tan sin lim 1 x x x x e → − − tan 0 lim x x x → + 3. 求 4.求

例题选解:07年考题 √1+xsinx-1 1.lim x→0 cosx-1 2.设函数 .2 f(x)= xsin二+k,x≠0 X 1, x=0 在x=0处连续,则k= A.-2B.-1 C.1 D.2
例题选解:07年考题 0 1 sin 1 lim x cos 1 x x → x + − = − 1. _. 2. 设函数 = + = 1, 0 , 0 2 sin ( ) x k x x x f x 在x = 0处连续,则k =_ A.-2 B.-1 C.1 D. 2

4.下列函数是无穷小的是 A、1+ 2, 当X→o0时,B、x+5x, 当x→0时, C、 2,当x→0D、2”,当x→0时 2.求0宁+子
2 1 1 2 x x + x → 2 x x5 x + x →0 1 2 x x →0 4.下列函数是无穷小的是_ ,当 B、 ,当 C、 ,当 2 x D、 ,当 x → 时. A、 时, 时, 2.求 1 1 2 0 2 lim[(1 ) ] 3 4 x x x x x − → + − − −