
第三章微分中值定理及其应用 本章教学目的:应用导数来研究函数本身所具有的 性质,如函数的增、减性及其极值;函数的凹、凸性及 其拐点等。 微分中值定理(包括罗尔定理、拉格朗日定理、柯 西定理)正是研究上述问题的有效工具。 本次课教学内容: (1)罗尔定理及其应用; (2)拉格朗日定理及其应用; (3)柯西定理及其应用
第三章 微分中值定理及其应用 本章教学目的:应用导数来研究函数本身所具有的 性质,如函数的增、减性及其极值;函数的凹、凸性及 其拐点等。 微分中值定理(包括罗尔定理、拉格朗日定理、柯 西定理)正是研究上述问题的有效工具。 本次课教学内容: (1)罗尔定理及其应用; (2)拉格朗日定理及其应用; (3)柯西定理及其应用
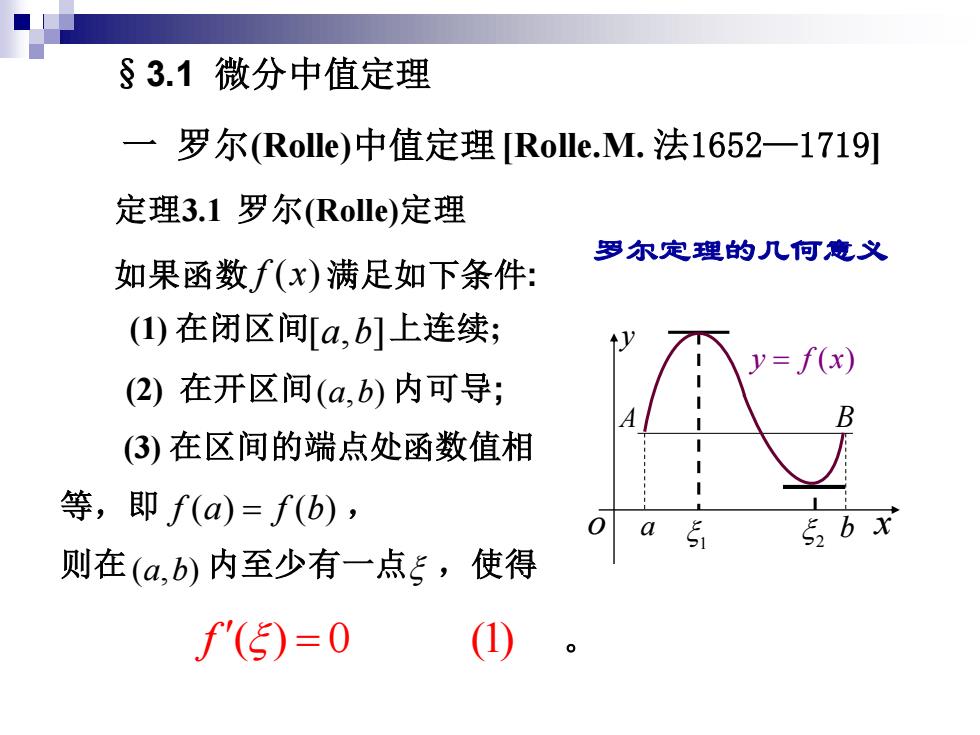
§3.1微分中值定理 一 罗尔(Rolle)中值定理Rolle.M.法1652一1719] 定理3.1罗尔(Rolle)定理 罗尔定理的几何意义 如果函数f(x)满足如下条件: ()在闭区间a,b]上连续; y=f(x) (2)在开区间(a,b)内可导; (3)在区间的端点处函数值相 等,即f(a)=f(b), a s 5,b x 则在(a,b)内至少有一点5,使得 f'(5)=0
§3.1 微分中值定理 一 罗尔(Rolle)中值定理 [Rolle.M. 法1652—1719] 定理3.1 罗尔(Rolle)定理 如果函数 f x( ) 满足如下条件: (1) 在闭区间 上连续; (2) 在开区间 内可导; (3) 在区间的端点处函数值相 等,即 , 则在 内至少有一点 ,使得 [ , ] a b ( , ) a b f a f b ( ) ( ) = ( , ) a b 几何意义: f ( ) 0 (1) = 。 罗尔定理的几何意义 a b A B y o x y f x = ( ) 1 2

有关知识点复习: 1、如果函数f(x)在闭区间[a,b]上连续,则f(x)在[a,b] 上必有最大值与最小值。 2、如果在x的δ去心邻域U(x,)内,f(x)≥0(或 f(x)≤0),而且1imf(x)=a,那么a≥0(或a≤0). 3、函数在一点可导的充分必要条件。 例1设f(x)=sinx,x∈[0,π],验证罗尔定理的正 确性。 解:(1)函数在区间[0,π]上连续; (2)函数在区间(0,)内可导;
有关知识点复习: 1、如果函数 在闭区间 上连续,则 在 上必有最大值与最小值。 f x( ) [ , ] a b f x( ) [ , ] a b 例1 设 , ,验证罗尔定理的正 确性。 f x x ( ) sin = x[0, ] 解:(1)函数在区间 [0, ] 上连续; (2)函数在区间(0, ) 内可导; 0 x 0 lim ( ) x x f x a → f (x) 0 ),而且 = ,那么 a 0 (或 a 0 ). o 0 2、 如果在 的 去心邻域 U x( , ) 内, f (x) 0 (或 3、函数在一点可导的充分必要条件
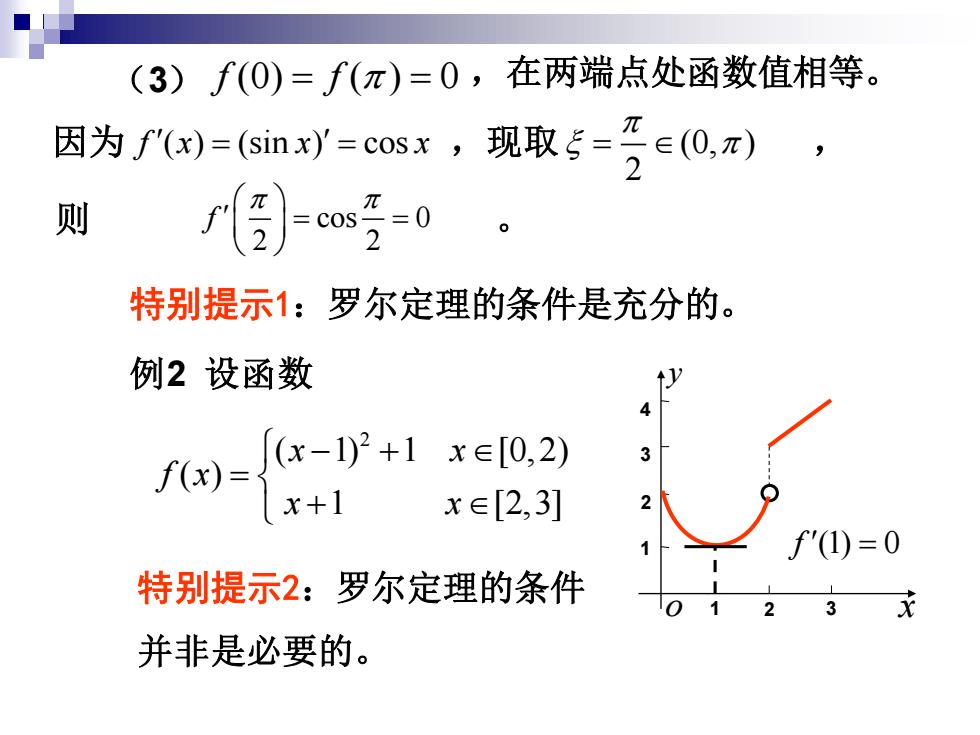
(3)f(0)=f(π)=0,在两端点处函数值相等。 因为f'(x)=((sin x)=cosx,现取5=-e(0,x) 则 元-2 cos-0 特别提示1:罗尔定理的条件是充分的。 例2设函数 4 (x-1)2+1x∈[0,2) f(x)= 3 x+1 x∈[2,3] 2 f'(1)=0 特别提示2:罗尔定理的条件 并非是必要的
(3) f f (0) ( ) 0 = = ,在两端点处函数值相等。 因为 f x x x ( ) (sin ) cos = = ,现取 (0, ) , 2 = 则 cos 0 。 2 2 f = = 特别提示1:罗尔定理的条件是充分的。 例2 设函数 2 ( 1) 1 [0, 2) ( ) 1 [2,3] x x f x x x − + = + 1 1 2 2 3 3 4 o x y 特别提示2:罗尔定理的条件 并非是必要的。 f (1) 0 =
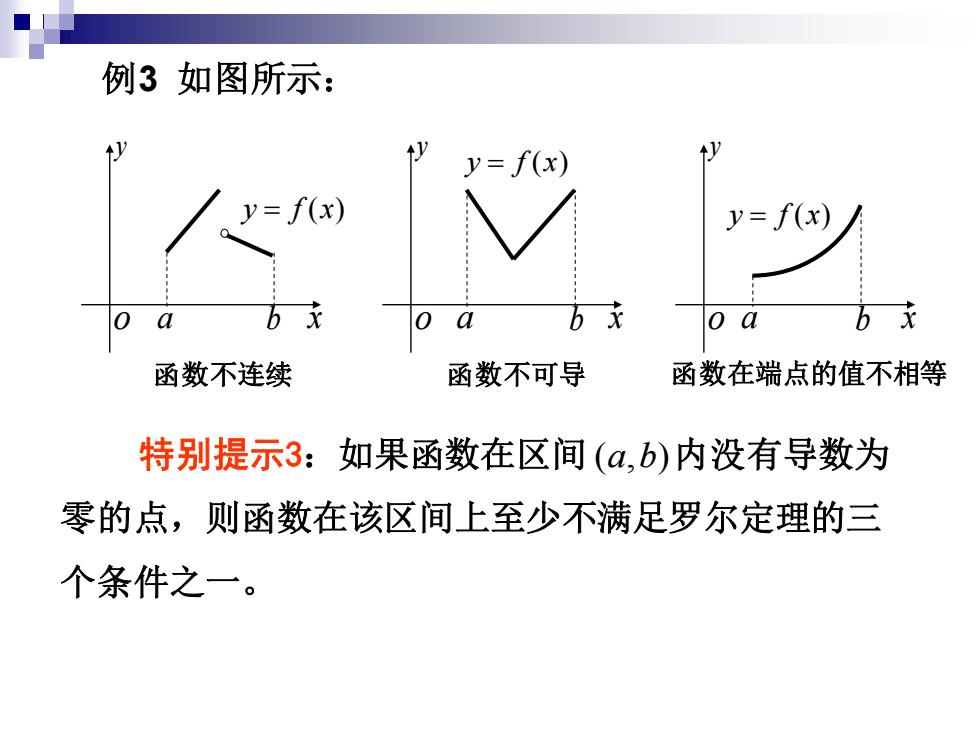
例3如图所示: y=f(x) y=f(x) y=f(x) a 0 o a bx 函数不连续 函数不可导 函数在端点的值不相等 特别提示3:如果函数在区间(α,b)内没有导数为 零的点,则函数在该区间上至少不满足罗尔定理的三 个条件之一
例3 如图所示: o x y a b y f x = ( ) 函数不连续 o x y a b y f x = ( ) 函数不可导 o x y a b y f x = ( ) 函数在端点的值不相等 特别提示3:如果函数在区间 内没有导数为 零的点,则函数在该区间上至少不满足罗尔定理的三 个条件之一。 ( , ) a b

例4如果方程 ax4+ax3+,x2+a,x=0有一个正根 x,证明方程4a,x2+3ax2+2a,x+a,=0至少有一个 小于x的正根。 例5设函数f(x)在[0,1]上可导,且f)=0, 证明:存在一点5∈(0,1),使得 f⑤)+号1)=0
小于 的正根。 4 3 2 0 1 2 3 a x a x a x a x + + + = 0 0 x 3 2 0 1 2 3 x0 4 3 2 0 a x a x a x a + + + = 例4 如果方程 至少有一个 有一个正根 ,证明方程 . 1 f f ( ) ( ) 0 + = f x( ) 在 [0,1] 上可导,且 f (1) 0 = (0,1) 例5 设函数 证明: 存在一点 , ,使得
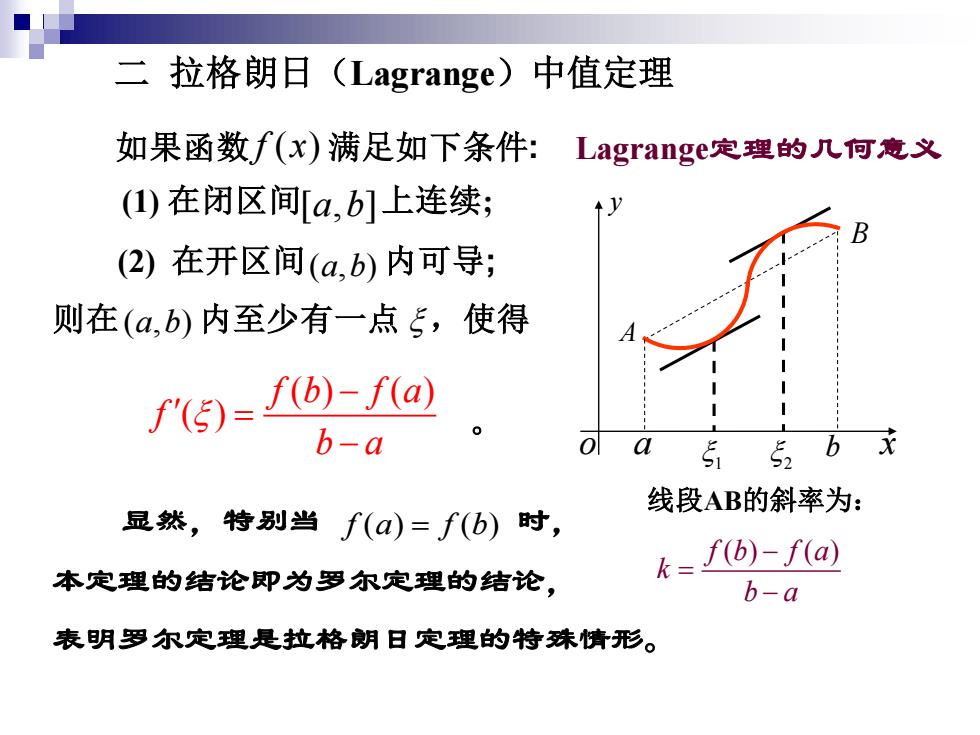
二 拉格朗日(Lagrange) 中值定理 如果函数f(x)满足如下条件:Lagrange定理的几何意义 (1)在闭区间[a,b]上连续; (2)在开区间(a,b)内可导; 则在(a,b)内至少有一点5,使得 M)=f(b)-f(a) b-a 51 5b元 线段AB的斜率为: 显然,特别当f(a)=f(b)时, 本定理的结论即为罗尔定理的结论, k=I(b)-f(a) b-a 表明罗尔定理是拉格朗日定理的特殊情形
二 拉格朗日(Lagrange)中值定理 如果函数 f x( ) 满足如下条件: (1) 在闭区间 上连续; (2) 在开区间 内可导; 则在 内至少有一点 ,使得 [ , ] a b ( , ) a b ( , ) a b ( ) ( ) ( ) f b f a f b a − = − 。 1 2 线段AB的斜率为: f b f a ( ) ( ) k b a − = − b B a A o x y Lagrange定理的几何意义 显然,特别当 时, 本定理的结论即为罗尔定理的结论, 表明罗尔定理是拉格朗日定理的特殊情形。 f a f b ( ) ( ) =

拉格朗日公式的三种等价形式: f(b)-f(a)=f'(5)(b-a), a<5<b; (3) f(b)-f(a)=f'(a+0(b-a)b-a),0<0<1;(4) f(a+h)-f(a)=f(a+oh)h, 0<0<1. (5) (4),(5)式又称为有限增量公式。 推论1若函数f在区间I上可导,且f'(x)=0,x∈I 则f为上的一个常量函数。 推论2若函数f与g均在区间1上可导,且 f'(x)三g'(x),x∈1,则在区间I上f与g只相差某一常 数,即f(x)=g(x)+c,(C为某一常数)
拉格朗日公式的三种等价形式: ( ) ( ) ( )( ), ; (3) ( ) ( ) ( ( ))( ),0 1; (4) ( ) ( ) ( ) , 0 1. (5) f b f a f b a a b f b f a f a b a b a f a h f a f a h h − = − − = + − − + − = + (4),(5)式又称为有限增量公式。 推论1 若函数 在区间 上可导,且 则 为 上的一个常量函数。 f I f x x I ( ) 0, f I 推论2 若函数 与 均在区间 上可导,且 ,则在区间 上 与 只相差某一常 数,即 f g I f x g x x I ( ) ( ), I f g f x g x c ( ) ( ) = + ,( c 为某一常数)

例5证明 arcsin x+arccosx= z.xcL-L 例6证明对一切h>-1,h≠0成立不等式 h<In(+h)<h 1+
例6 证明对一切 h h − 1, 0 成立不等式 ln(1 ) 1 h h h h + + 例5 证明 arcsin arccos , 1,1 . 2 x x x + = −

三柯西(Cauchy)中值定理 如果函数f(x),F(x)满足如下条件: (1)在闭区间[a,b]上连续; (2)在开区间(a,b)内可导; (3)F(x)≠0, 则在(a,b)内至少有一点5,使得 f(b)-f(a_f'() F(b)-F(a) F'(E) 。 例7当x>0时,证明e>1+x
如果函数 f x F x ( ), ( ) 满足如下条件: ( ) ( ) ( ) ( ) ( ) ( ) f b f a f F b F a F − = − 。 三 柯西(Cauchy)中值定理 (1) 在闭区间 上连续; (2) 在开区间 内可导; (3) 则在 内至少有一点 ,使得 [ , ] a b ( , ) a b ( , ) a b F x( ) 0, 例7 当 x 0 时,证明 1 x e x +