
第七章多元函数微分学 A级自测题 一、填空题(2×6=12分) 1.函数:=ln(y)的定义域是 2.设:=x+y+f(x-y),且当y=0时,=x2.则fx)=一,x,)=一·一 3.m 4.设函数:=y,则,=一= 5.f(x,y)在点(x,y)可微分是f(x,y)在该点连续的 条件.∫(x,y)在点(x,y)连续是 f(x,y)在该点可微分的条件. 6.函数fx,)=x2+y+y2+x-y+1的极值 二、单选题(2×5=10分) 1.若f(x,)在点(xoo)处连续,则Iimf(x,)() (A)存在:(B)不存在:(C)不确定:D)以上均不正确. 2.函数:=arctan二的全微分() y *@湾,o浩@ x2+y2 (A)e2:B)0;(Ce:(D)1. 4设=停,则dL等于(。 W停:国本得:《©点-:D,a-海 5.=sinsin yin:在条件x++:-号(>0,>0:>0下的最大值(, )g®)石 (C)1;(D)0. 三、计算题(58分)
1 第七章 多元函数微分学 A 级自测题 一、填空题(2 6=12 分) 1.函数 z xy = ln( ) 的定义域是 . 2.设 z x y f x y = + + − ( ) ,且当 y = 0 时, 2 z x = .则 f x( ) = , z x y ( , ) = . 3. ( , ) (0,5) lim x y sin x → xy = . 4.设函数 x z y = ,则 _, _. x y z z = = 5. f (x, y) 在点 (x, y) 可微分是 f (x, y) 在该点连续的 条件. f (x, y) 在点 (x, y) 连续是 f (x, y) 在该点可微分的 条件. 6.函数 ( , ) 1 2 2 f x y = x + xy + y + x − y + 的极值 . 二、单选题(2 5=10 分) 1.若 f (x, y) 在点 ( , ) 0 0 x y 处连续,则 0 0 lim ( , ) x x y y f x y → → ( ) (A) 存在; (B) 不存在; (C) 不确定; (D) 以上均不正确. 2.函数 y x z = arctan 的全微分( ) (A) 2 2 x y xdx ydy + − ; (B) 2 2 x y ydx xdy + − ; (C) 2 2 2 (x y ) ydx xdy + − ; (D) 2 2 2 2 x y y dx x dy + − . 3. 2 1 1 lim(1 ) x x y x y x + → → + 为( ). (A) 2 e ; (B) 0 ; (C) e; (D) 1. 4.设 1 ( , , ) ( )z x f x y z y = ,则 d f (1, 1, 1) 等于( ). (A) 1 1 ( )z x dx dy y y − ;(B) dy y x dx y x z 2 1 − ; (C) dx − dy ;(D) ydx − xdy. 5. u x y z = sin sin sin 在条件 ( 0, 0, 0) 2 x + y + z = x y z 下的最大值( ). (A) 8 1 ; (B) 6 1 ; (C) 1 ; (D) 0. 三、计算题(58 分)

1.求函数:=-不的定义域,并求极限1m:.(6分) 2.求下列极限(9分) 上》职 器. sn xy 3.求下列函数的一阶和二阶偏导数:(8分) y 4求:”:当x=2y-1A如=014=-02时的全增量和全微分.《6分) 5求会器6分 6.设u=,而x=0y=v0都是可微函数,求安(5分》 g橙:=心-.会容6分》 9.设:=f(x,)是由方程:-y-x+xe-=0所确定的函数,求.(6分) 四、应用题(20分) 1果内接于箱球++=1的大长方的体机,长方的各个面平行干坐标面。 2.设某工厂生产A和B两种产品,产量分别为x和y(单位:千件),利润函数为 L(x,)=6x-x2+16y-4y2-2,已知生产这两种产品时,每千件产品均需消耗某种原料2000 金展者线吸料如公斤。问而种产品各生产多少千件针8眼大:是大润方 自我测试题B 一、填空题(2×8=16分) 1.己知fx,e2)=x-y,则fx,)=·
2 1.求函数 z = x − y 的定义域,并求极限 1 2 0 lim x y z → → .(6 分) 2. 求下列极限(9 分) (1) 2 2 2 2 2 2 0 0 1 cos( ) lim ( ) x y x y → x y x y → − + + ,(2) 3 3 ( , ) (0,1) 1 2 lim x y xy x y + − → ,(3) 1 1 sin lim 0 0 → + − → xy xy y x . 3.求下列函数的一阶和二阶偏导数:(8 分) (1) y xe z y = , 求 y z x z , .(2) z y x y = + cos sin ,求 x y z y z x z 2 2 2 2 2 , , . 4.求 2 2 xy z x y = − ,当 x y x y = = = = − 2, 1, 0.1, 0.2 时的全增量和全微分.(6 分) 5. z xy = sin( ) ,求 2 , z z x x y .(6 分) 6. 设 y u x 2 = ,而 x = (t), y = (t) 都是可微函数,求 dt du .(5 分) 7. 设 uv z = e , x y u ln x y , v arctan 2 2 = + = ,求 y z x z , .(6 分) 8. 设 3 3 ( , ) xy z f x y e = − ,求 y z x z , .(6 分) 9. 设 z = f (x, y) 是由方程 0 z y x z y x xe − − − − + = 所确定的函数,求 dz .(6 分) 四、应用题(20 分) 1.求内接于椭球 1 2 2 2 2 2 2 + + = c z b y a x 的最大长方体的体积,长方体的各个面平行于坐标面. 2.设某 工厂生 产 A 和 B 两种产品 ,产量 分别为 x 和 y (单位: 千件 ), 利润函 数为 ( , ) 6 16 4 2 2 2 L x y = x − x + y − y − ,已知生产这两种产品时,每千件产品均需消耗某种原料 2000 公斤,现有该原料 12000 公斤,问两种产品各生产多少千件时,总利润最大?最大利润为多 少? 自我测试题 B 一、填空题(2 8=16 分) 1.已知 f x e x y y ( , ) = − 2 ,则 f x y ( , ) _ = .

2细2-回+4 y 3设:由:”=0所确定,则- 4设u=又y=x1=,则密 5.设u=0-,而y=amx:=0sx则血 a2+1 d 6设功=+(-am得则0小- 1降研设:动++小和具者三路法续号数测高-一 8.函数:=y+50+20(x>0,y>0)的极小值为 二、选择题(2×6=12分) e(之 (A)1(B)-1(C)0 (D)a 20侧所度u=6动宁则需在点心宁处的值人 wg@c)!D月 e 3.若ye=-以则会学的值为(》 (A)-1(B)2 (C)1 D)-2 4.(05研)设有三元方程y-ny+e=1,根据隐函数存在定理,存在点(0,1,)的一个邻域, 在此邻域内该方程(. (A)只能确定一个具有连续偏导数的隐函数:=(x,). (B)可确定两个具有连续偏导数的隐函数y=(x,)和:=(x,y). (C)可确定两个具有连续偏导数的隐函数x=xy,)和z=(xy). (D)可确定两个具有连续偏导数的隐函数x=x(y,)和y=(x,) 5.(02研)考虑二元函数f(x,)的下面4条性质: 3
3 2. 0 0 2 4 lim _ x y xy → xy → − + = . 3.设 z x y ( , ) 由 2 2 0 xy z x y − = − 所确定,则 dz = _ . 4.设 u = f (x, y,z) ,又 y = (x,t), t = (x,z) ,则 _ u x = . 5.设 1 ( ) 2 + − = a e y z u ax ,而 y = asin x, z = cos x, 则 _ du dx = . 6.设 y x f (x, y) = x + ( y −1) arcsin ,则 (0,1) _ x f = . 7.(98 研)设 ( ) ( ) 1 f xy y x y x z = + + , f , 具有二阶连续导数,则 2 z x y = . 8.函数 ( 0, 0) 50 20 = + + x y x y z xy 的极小值为 . 二、选择题(2 6=12 分) 1. 0 sin( ) lim x y a xy → xy → = ( ). (A) 1 (B) −1 (C) 0 (D) a 2.(94 研) 设 y x u e x sin − = , 则 x y u 2 在点 1 (2, ) 处的值为( ). (A) e (B) 2 ( ) e (C) e 1 (D) 1 3.若 y − nz = f (x − mz), 则 y z n x z m + 的值为( ). (A) -1 (B)2 (C) 1 (D) -2 4.(05 研) 设有三元方程 ln 1 xz xy z y e − + = ,根据隐函数存在定理,存在点 (0,1,1) 的一个邻域, 在此邻域内该方程( ). (A)只能确定一个具有连续偏导数的隐函数 z = z(x, y) . (B)可确定两个具有连续偏导数的隐函数 y = y(x,z) 和 z = z(x, y) . (C)可确定两个具有连续偏导数的隐函数 x = x( y,z) 和 z = z(x, y) . (D)可确定两个具有连续偏导数的隐函数 x = x( y,z) 和 y = y(x,z) . 5.(02 研) 考虑二元函数 f (x, y) 的下面 4 条性质:

(1)fx,y)在(x,)处连续,(2)f(x,y)在(x,)处的两个偏导数连续, (3)fx,)在(,)处可微,(④,)在(x,)处的两个偏导数存在. 若用"p一g"表示可由性质p推出性质q,则有正确的是(). (A)2)→3)→1)(B)3)→2)=1),(C)3)→4)→),(D)3)→1)→4) 6.设:=fxy)在点(x,)处取得极小值,则(x)=fx,)在x处(). (A)取得最小值(B)取得极大值(C)取得最大值(D)取得极小值 三、计算题(56分) 1.求下列复合函数的偏导数(9分) 》设:=+,器房 a)==e,而:=a,求器影 g》设2+-网其中p可微。求器 2设/-eac-很,球Ann.9分 3.设:=fx4W=x0smr+ec0sm,而u=yv=x+y,求张.(6分) 4整学警6 5.00研)已知:=心,u=h2+,v=acan上,求t.(8分) 6.试求函数:=x(4-x-y)在x=1y=0,x+y=6所围的闭区域上的最大值点与最小值点, 以及其相应的最大值与最小值.(8分) 7.(05研)设:=x,)是由x2-6xy+10y2-22-2+18=0确定的函数,求:=(x,)的极 值点和极值.(10分) 四、应用题 某电视机厂生产的电视机同时在两个市场销售,售价分别为P和P:销售量分别为q,利 92:需求函数分别为9-12-0.1p,92-2-0.01p2:总成本函数为C=35+40(q+92).试问厂 家如何确定两个市场的售价,才能使获得的利润最大?最大总利润是多少?(10分)
4 (1) f (x, y) 在 ( , ) 0 0 x y 处连续,(2) f (x, y) 在 ( , ) 0 0 x y 处的两个偏导数连续, (3) f (x, y) 在 ( , ) 0 0 x y 处可微,(4) f (x, y) 在 ( , ) 0 0 x y 处的两个偏导数存在. 若用 " " p q 表示可由性质 p 推出性质 q ,则有正确的是( ). (A) 2) 3) 1) (B) 3) 2) 1) , ( ) 3) 4) 1) C , ( ) 3) 1) 4) D . 6.设 z = f (x, y) 在点 ( , ) 0 0 x y 处取得极小值,则 ( ) ( , ) 0 x = f x y 在 0 x 处( ). (A) 取得最小值 (B)取得极大值 (C) 取得最大值 (D)取得极小值 三、计算题(56 分) 1.求下列复合函数的偏导数(9 分) (1) 设 xy x y z x y e 2 2 ( ) 2 2 + = + ,求 y z x z , . (2) 2 2 2 ( , , ) x y z u f x y z e + + = = ,而 2 z x y = cos ,求 y u x u , . (3) 设 2 2 ( ) z x z y y + = ,其中 可微,求 y z . 2.设 ( , ) sin ( 1)arctan xy x f x y e y x y = + − ,试求 (1,1), x f (1,1), y f df (1,1) .(9 分) 3.设 z f x u v xe v e v u u = ( , , ) = sin + cos ,而 u = xy, v = x + y ,求 x z .(6 分) 4.若 y x u = z arctan ,求 222 2 2 2 uuu x y z + + .(6 分) 5.(00 研) 已知 x y z u u x y v v , ln , arctan 2 2 = = + = ,求 dz .(8 分) 6.试求函数 z = xy(4 − x − y) 在 x = 1, y = 0, x + y = 6 所围的闭区域上的最大值点与最小值点, 以及其相应的最大值与最小值.(8 分) 7.(05 研) 设 z = z(x, y) 是由 6 10 2 18 0 2 2 2 x − xy + y − yz − z + = 确定的函数,求 z = z(x, y) 的极 值点和极值.(10 分) 四、应用题 某电视机厂生产的电视机同时在两个市场销售,售价分别为 1 p 和 2 p ;销售量分别为 1 q 和 2 q ;需求函数分别为 1 1 2 2 q p q p = − = − 12 0.1 , 2 0.01 ;总成本函数为 1 2 C q q = + + 35 40( ) .试问厂 家如何确定两个市场的售价,才能使获得的利润最大?最大总利润是多少?(10 分)
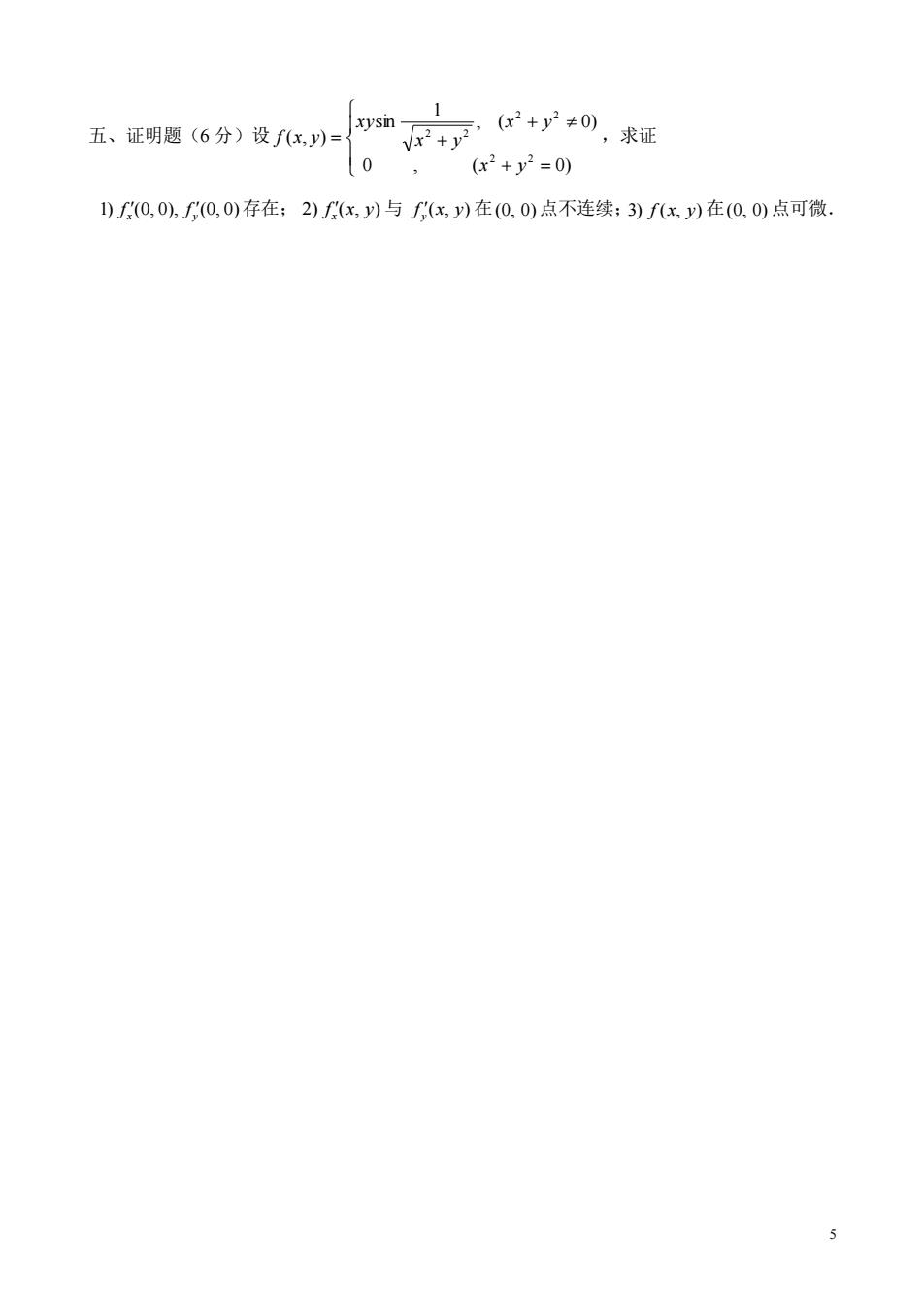
1 五、证明题(6分)设(x,y)= 0mF+可+广0,求证 0,(x2+y2=0) )f0,0),f0,0)存在:2)x,y)与fxy)在(0,0)点不连续:3)fx)在(0,0)点可微
5 五、证明题(6 分)设 + = + = + 0 , ( 0) , ( 0) 1 sin ( , ) 2 2 2 2 2 2 x y x y x y x y f x y ,求证 1) (0, 0), (0, 0) x y f f 存在; 2) ( , ) x f x y 与 ( , ) y f x y 在 (0, 0) 点不连续; 3) f (x, y) 在 (0, 0) 点可微.